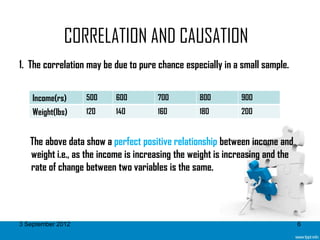
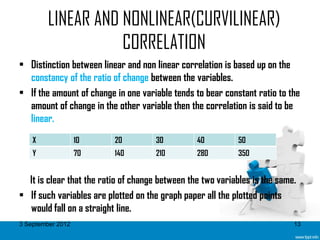
The document discusses the concept of correlation, specifically linear correlation. It provides definitions of correlation from various sources and explains that correlation refers to the relationship between two or more variables. The degree of this relationship is measured by the correlation coefficient. Common types of correlation are discussed such as positive and negative correlation. Methods for studying correlation are also outlined, including scatter diagrams and Karl Pearson's coefficient of correlation.

1. CORRELATION
(LINEAR)
3 September 2012 1

2. CORRELATION
 If two quantities vary in such a way that movements of one are
accompanied by movements of others then these quantities are said to
be correlated.
 Ex: relationship between price of commodity and amount demanded,
Increased in amount of the rainfall and the production of rice
 The degree of relationship between variables under consideration is
measured through the correlation analysis.
 The measure of correlation is called the correlation coefficient or
correlation index ( usually denoted by r or ρ )
 The correlation analysis refers to the techniques used in measuring the
closeness of the relationship between the variables.
3 September 2012 2

3. DEFINITIONS
• Correlation analysis deals with the association between two or more
variables.
Simpson and Kafka
• Correlation is an analysis of co variation between two or more variables.
A.M.Tuttle
• If two or more quantities were in sympathy so that the movement of one
tend to be accompanied by the corresponding movements in the other
then they are said to be correlated
L.R.Conner
3 September 2012 3

4. ANALYSIS
• The problem of analyzing the relation between different series should be
broken down in to three steps
1. Determining whether a relation exists and if it does, measuring it.
2. Testing whether it is significant.
3. Establishing the cause and effect relation if any.
3 September 2012 4

5. SIGNIFICANCE OF THE STUDY OF CORRELATION
 Most of the variables show some kind of relationship
 Once we know that two variables are closely related we can estimate
the value of one variable given the value of another.
 Correlation analysis contributes to the understanding of the economic
behavior
 The effect of correlation is to reduce the range of uncertainty
3 September 2012 5

6. CORRELATION AND CAUSATION
1. The correlation may be due to pure chance especially in a small sample.
Income(rs) 500 600 700 800 900
Weight(lbs) 120 140 160 180 200
The above data show a perfect positive relationship between income and
weight i.e., as the income is increasing the weight is increasing and the
rate of change between two variables is the same.
3 September 2012 6

7. 2. Both the correlated variables may be influenced by one or more other
variables.
3. Both the variables may be mututally influencing each other so that neither
can be designated as the cause and the other the effect.
Correlation observed between variables that cannot conceivably be
casually related is called spurious or nonsense correlation
3 September 2012 7

8. TYPES OF CORRELATION
Positive or negative
Linear and non linear correlation
Simple , partial and multiple correlation
3 September 2012 8

9. POSITIVE OR NEGATIVE CORRELATION
• Whether the correlation is positive or negative would depend up on the
direction of the change of the variable.
• If both the variables are varying in the same direction , then the
correlation is said to be positive.
• If the variables are varying in opposite direction the correlation is said to
be negative
3 September 2012 9

10. Positive correlation
X 10 12 15 18 20
Y 15 20 22 25 37
Y-Values
40
35
30
25
20
15
10
5
0
0 5 10 15 20 25
3 September 2012 10

11. Negative correlation
X 20 30 40 60 80
Y 40 30 22 15 10
Y-Values
45
40
35
30
25
20
15
10
5
0
0 20 40 60 80 100
3 September 2012 11

12. SIMPLE PARTIAL AND MULTIPLE CORRELATION
• The distinction between simple partial and multiple correlation is based
up on the number of variables studied.
• When only two variables are studied it is a problem of simple correlation
• When three or more variable are studied it is problem of either multiple
or partial correlation.
• In multiple correlation three or more variables are studied
simultaneously.
• On the other hand in partial correlation we recognize more than two
variables but consider only two variables to be influencing each other the
effect of other influencing variable kept constant.
3 September 2012 12

13. LINEAR AND NONLINEAR(CURVILINEAR)
CORRELATION
• Distinction between linear and non linear correlation is based up on the
constancy of the ratio of change between the variables.
• If the amount of change in one variable tends to bear constant ratio to the
amount of change in the other variable then the correlation is said to be
linear.
X 10 20 30 40 50
Y 70 140 210 280 350
It is clear that the ratio of change between the two variables is the same.
• If such variables are plotted on the graph paper all the plotted points
would fall on a straight line.
3 September 2012 13

14. 400
350
300
250
200
150
100
50
0
0 10 20 30 40 50 60
3 September 2012 14

15. Correlation would be called non linear or curvilinear if the amount of
change in one variable does not bear a constant ratio with the amount of
change in the other variable.
3 September 2012 15

16. METHODS OF STUDYING CORRELATION
1. Scatter diagram
2. Graphic method
3. Karl Pearson’s coefficient of correlation.
4. Concurrent Deviation Method
5. Method of least squares
3 September 2012 16

17. SCATTER DIAGRAM METHOD
• The simplest device for ascertaining if the two variables are related is to
prepare a dot chart called scatter diagram.
• When this method is used the given data are plotted on a graph paper in
the form of dots. I.e., for each pair of X and Y values we put a dot and thus
obtain as many points as the number of observations.
• By looking to the scatter of the various points we can form an idea as to
whether the variables are related or not.
• The greater the scatter of the plotted points on the chart the lesser is the
relationship between the two variables
• The more closely the points come to the straight line higher the degree of
relationship.
3 September 2012 17

18. • If all the points lie on a straight line falling from the lower left hand
corner to the upper right hand corner the correlation is said to be
perfectly positive(r=1)
8
7
6
5
4
3
2
1
0
0 2 4 6 8
3 September 2012 18

19. If all the points are lying on a straight line rising from the upper left hand
corner to the lower right hand corner of the diagram correlation is said to
be perfectly negative.
8
7
6
5
4
3
2
1
0
0 1 2 3 4 5 6 7 8
3 September 2012 19

20. • If the plotted points fall in a narrow band there would be a high degree of
correlation between the variables.
• If the points are widely scattered over the diagram it indicates very little
relation ship between the variables.
10 10
8 8
6 6
4 4
2 2
0 0
0 5 10 0 5 10
HIGH DEGREE OF POSITIVE CORRELATION LOW DEGREE OF POSITIVE CORRELATION
3 September 2012 20

21. If the plotted points lie in a haphazard manner it shows the absence of any
relationship between the variables
8
7
6
5
4
3
2
1
0
0 2 4 6 8 10 12 14
3 September 2012 21

22. EXAMPLE:
X 2 3 5 6 8
Y 6 5 7 8 12
14
12
10
8
6
4
2
0
0 2 4 6 8 10
3 September 2012 22

23. • By looking at the scattered diagram we can say that the variables x and y
are correlated. Further the correlation is positive because the trend of
the points is upward rising from the lower left hand corner to the upper
right hand corner of the diagram.
• It also indicates that the degree of relationship is higher because the
plotted points are near to the line which shows perfect relationship
between the variables.
3 September 2012 23

24. MERITS AND LIMITATIONS
MERITS
• It is a simple and non mathematical method of studying correlation
between variables.
• As such it can be easily understood and a rough idea can very quickly be
formed as to whether or the variables are related.
• It is the first step in investigating relationship between 2 variables.
LIMITATIONS:
• By applying this method we can get an idea about the direction of
correlation and also whether it is high or low
• But we cannot establish the exact degree of correlation between the
variables as is possible by applying the mathematical methods.
3 September 2012 24

25. GRAPHIC METHOD
• When this method is used the individual values of the two variables are
plotted on the graph paper.
• We thus obtain 2 curves. One for x variable and another for y variable.
• By examining the direction and closeness of the two curves so drawn we
can infer if the variables are related or not.
• If both the curves drawn on the graph are moving in the same direction
(either upward or downward)then the correlation is said to be positive.
• On the other hand if the curves are moving in the opposite direction
correlation is said to be negative.
3 September 2012 25

26. Year Average income Average
expenditure
1979 100 90
1980 102 91
1981 105 93
1982 105 95
1983 101 92
1984 112 94
3 September 2012 26

27. 120
INCOME
100
EXPENDITURE
80
60 Series 1
Series 2
40
20
0
1979 1980 1981 1982 1983 1984
3 September 2012 27

28. KARL PEARSON’S COEFFICIENT OF CORRELATION
• Among several mathematical methods of measuring correlation, the Karl
Pearson’s method, popularly known as Pearson’s coefficient of
correlation, is most widely used in practice
• It is denoted by the symbol ρ or r
3 September 2012 28

29. CORRELATION COEFFICIENT
• If [X,Y] is a two dimensional random variable, the correlation coefficient, denoted
r, is
ρ=Cov(X,Y) ∕ Var(X) . Var(Y) = σXY ∕ σX σY
• This is also called as PEARSON CORRELATION COEFFICIENT
ρ= ∑xy ∕ √ (∑x2 * ∑y2) = ∑xy ∕ N σX σY , where
x=(X-X’) ; y=(Y-Y’)
σX = Standard Deviation of X and
σY = Standard Deviation of Y
N = no of pairs of observation
3 September 2012 ρ = correlation coefficient 29

30. STEPS TO CALCULATE CORRELATION COEFFICIENT
• Take the deviations of X from the mean of X and denote by x
• Square these deviations and obtain the total i.e., Σx2
• Take the deviations of Y from the mean of Y and denote by y
• Square these deviations and obtain the total i.e., Σy2
• Multiply the deviations of X and Y and obtain the total i.e., Σxy
• Substitute the values in the formula
3 September 2012 30

31. EXAMPLE
• Calculate the Karl Pearson’s Correlation Coefficient from the following
data and interpret it’s value
Roll no of students: 1 2 3 4 5
Marks in Accountancy : 48 35 17 23 47
Marks in Statistics: 45 20 40 25 45
SOLUTION:
Let marks in Accountancy be denoted by X and Statistics by Y
3 September 2012 31

32. Roll no X (X-34) x2 Y (Y-35) y2 xy
x y
1 48 14 196 45 10 100 140
2 35 1 1 20 -15 225 -15
3 17 -17 289 40 5 25 -85
4 23 -11 121 25 -10 100 110
5 47 13 169 45 10 100 130
∑X=170 ∑x=0 ∑x2=776 ∑Y=175 ∑y=0 ∑y2=550 ∑xy=280
3 September 2012 32

33. • The Pearson’s coefficient of correlation is
ρ= ∑xy ∕ √(∑x2 *∑y2)
where x=(X-X’); y=(Y-Y’) , X'= ∑X ∕ N; Y’=∑Y ∕ N
∑xy=280 ∑x2=776 ∑y2=550
ρ = 280 ∕ √ (776 * 550)
= 0.496
3 September 2012 33

34. DEGREE OF CORRELATION
• The value of ρ always lies between -1 and 1.
• If ρ lies between 0 and 1, it is positive. Else, if it lies between -1 and 0, it is
negative
• If ρ=1, then the two variables are said to be perfect positively correlated
• If ρ=-1, then the two variables are said to be perfect negatively
correlated
• If ρ=0, then the two variables are not correlated
3 September 2012 34

35. 3 September 2012 35