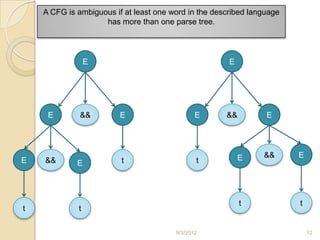
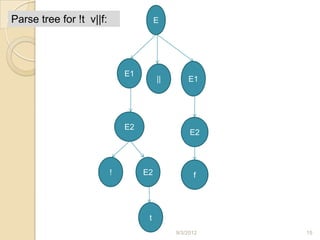
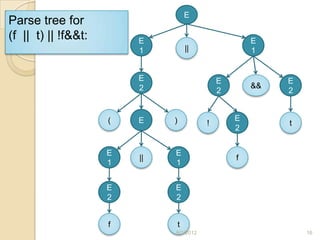
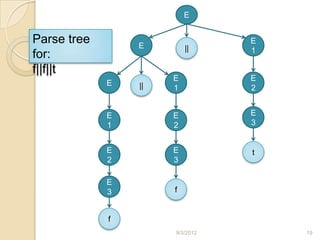
The document discusses parsing in compilers. It defines parsing as the second stage after lexical analysis, where a parser checks if the stream of tokens from the lexical analyzer is grammatically correct by generating a parse tree. The fundamental theory behind parsing is context-free grammar, which is used to define languages and check parsing. The document then discusses context-free grammars, parse trees, ambiguity, and provides examples of grammars for Boolean expressions to illustrate parsing concepts.

1. PARSING
9/3/2012 1

2. PARSING
 In the design of a compiler the second stage after
lexical analysis is parsing. It is also called as syntax
analysis.
 Parser will take the stream of tokens generated by
the lexical analyzer , check if it is grammatically
correct and generate a parse tree.
 The fundamental theory behind parsing is grammar
theory.
9/3/2012 2

3. CONTEXT FREE GRAMMAR
 A CFG, G=(N, T, P, S) where:
 N is a set of non-terminals.
 T is a set of terminals.
 P is a set of productions (or rules) which are given by
A->α
where A denotes a single non-terminal.
α denotes a set of terminals and non-
terminals.
 S is the start state. If not specified, then it is the non-
terminal that appears on the left-hand side of the first
production.
9/3/2012 3

4. Parse trees
Parse trees are labeled trees characterized by
the following:
– The root is labeled by the start symbol.
– Each leaf is labeled by a token or !.
– Each interior node is labeled by a non-
terminal.
– If A is the non-terminal labeling some interior
node and X1, X2, …, Xn are the labels of the
children of that node from left to right, then
A ::= X1, X2, …, Xn
is a production in the grammar.
9/3/2012 4

5. AMBIGUITY AND UNAMBIGUITY :
 A word is said to be ambiguously derivable if there
are more than one derivations existing for the
word, that is if there are more than one distinct
parse tree generated for that word.
There are two kinds of derivations that are important.
•A derivation is a leftmost derivation if it is always the
leftmost non-terminal that is chosen to be replaced.
•It is a rightmost derivation if it is always the rightmost
one.
Ambiguity is considered only when words are derived
using the same kind of derivation.
9/3/2012 5

6. AMBIGUITY AND UNAMBIGUITY
 A grammar is said to be ambiguous if there exists
at least one word which is ambiguously derivable.
 A grammar is said to be unambiguous if all the
words derived from it are unambiguous.
9/3/2012 6

7.  A language L is said to be unambiguous if there
exists at least one grammar which is unambiguous.
 A language L is said to be ambiguous if all the
grammar of the language are ambiguous.
Programming language grammars must be
unambiguous.
9/3/2012 7

8. BOOLEAN EXPRESSIONS
The language of Boolean expressions can be defined in
English as follows:
 true is a Boolean expression.
 false is a Boolean expression.
 If exp1 and exp2 are Boolean expressions, then so are
the following:
• expression1 OR expression2
• expression1 AND expression2
• NOT expression1
Low  ||
• ( expression1 ) Higher  &&
Highest !
9/3/2012 8

9. Consider this simple CFG:
 bexp  TRUE
 bexp  FALSE
 bexp  bexp || bexp
 bexp  bexp && bexp
 bexp  ! bexp
 bexp  ( bexp )
9/3/2012 9

10. CONTEXT FREE GRAMMAR FOR
BOOLEAN EXPRESSIONS
Consider the following short hand form of the CFG
for Boolean expressions:
 E  E && E
 E  E || E
E!E
 E  (E)
Et
Ef
 E is a non-terminal and the start symbol.
 &&, ||, !, (, ), t and f are terminals.
9/3/2012 10

11. Here are two different (leftmost derivations).
• The first one, corresponding to the first tree:
E => E && E
=> E && E && E
=> t && E && E
=> t && t && E
=> t && t && t
• The second one, corresponding to the second
tree:
E => E && E
=> t && E
=> t && E && E
=> t && t && E
=> t && t && t
9/3/2012 11

12. A CFG is ambiguous if at least one word in the described language
has more than one parse tree.
E E
E && E E && E
E && E
E && E t t
t t
t t
9/3/2012 12

13.  We construct an unambiguous version of the
context-free grammar for Boolean expressions by
making it reflect the following operator precedence
conventions:
 ! (NOT) has the highest precedence
 && (AND) has the next highest precedence
 || (OR) has the lowest precedence
 For example, t v ~f ^ t should be interpreted as
t v ((~f)^t). As long as the grammar is
unambiguous, you can choose whether or not to
accept expressions that would need conventions
about operator associatively to disambiguate
them, like t ^ t ^ t.
9/3/2012 13

14.  Here is a version that assumes that the binary operators
are non- associative.
◦ E  E1 || E1
◦ E  E1
◦ E1  E2 && E2
◦ E1  E2
◦ E2  ! E2
◦ E2 (E )
◦ E2  t
◦ E2 f
 Draw the derivation trees according to your
unambiguous grammar for the following two
expressions:
◦ (i) ! t || f
◦ (ii) (f || t) || ! f && t 9/3/2012 14

15. Parse tree for !t v||f: E
E1
|| E1
E2
E2
! E2 f
t
9/3/2012 15

16. E
Parse tree for
(f || t) || !f&&t: E E
1 || 1
E E E
2 &&
2 2
( E ) E
! t
2
E E
|| f
1 1
E E
2 2
f t
9/3/2012 16

17. ASSOCIATIVITY
The binary operators && and || are be
considered to be left-associative in most
programming languages.
 i.e. an expression like t || t || t would be interpreted
as (t || t) || t
Short Circuit
9/3/2012 17

18. Making the production rules for the binary
operators left associatively:
E  E || E1
E  E1
E1 E1 && E2
E1 E2
E2 !E3
E2 E3
E3 ( E )
E3 T
E3 F
9/3/2012 18

19. E
Parse tree E
E
|| 1
for:
f||f||t
E E
E || 1 2
E E E
1 2 3
E E t
2 3
E
3 f
f
9/3/2012 19

20. THANK
YOU..
9/3/2012 20