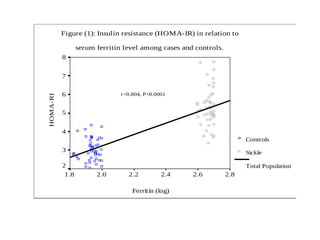
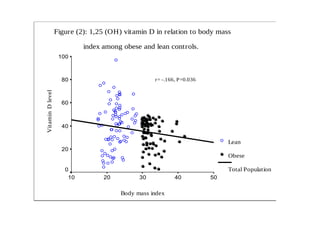
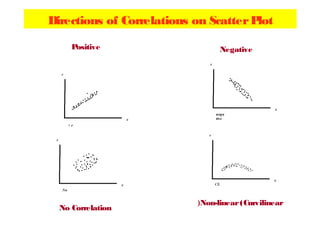
The document discusses the concept of correlation between variables, categorizing them into dependent and independent types. It details various methods for analyzing relationships, including tabular, graphical, and numerical techniques, and explains how to interpret correlation coefficients and statistical significance. Examples are provided to illustrate correlation calculation and relationships in data, including positive, negative, and no correlation scenarios.

1. 05/04/14 Dr Tarek Amin 1
Investigating the Relationship
between Two orMore Variables
(Correlation)
Professor Tarek Tawfik Amin
Public Health, Faculty of Medicine
Cairo University
amin55@myway.com

2. The Relationship Between Variables
Variables can be categorized into two types when investigating
their relationship:
Dependent:
A dependent variable is explained oraffected
by an independent variable. Age and height
Independent :
Two variables are independent if the pattern of
variation in the scores forone variable is not
related orassociated with variation in the scores
forthe othervariable.
The level of education in Ecuadorand the infant
mortality in Mali

3. Techniques used to Analyze the Relationship between Two
Variables
Method Examples
I- Tabularand graphical methods:
These present data in way that reveals a
possible relationship between two
variables.
II-Numerical methods:
Mathematical operations used to quantify,
in a single number, the strength of a
relationship (measures of association).
When both variables are measured at least
at the ordinal level they also indicate the
direction of the relationship.
Bivariate table for categorical data
(nominal/ordinal data)
Scatter plot for interval/ratio.
Lambda, Cramer’s V (nominal)
Gamma, Somer’s d, Kendall’s tau-b/c
(ordinal with few values)
Spearman’s rank order Co/Co.
(ordinal scales with many values)
Pearson’s product moment correlation
(Interval/ratio)
These techniques are called collectively as
Bi-variate descriptive statistics

4. Correlation: indications
o Correlational techniques are used to study
relationships.
o They may be used in exploratory studies in
which one to intent to determine whether
relationships exist,
o And in hypothesis testing about a particular
relationship.

5. Correlations techniques used to
assess
the existence,
the direction
and the strength
of association between
variables.

6. Pearson Correlation (Numeric, interval/ratio)
The Pearson product moment correlation coefficient (rorrho)
is the usual method by which the relation between two
variables is quantified.
Type of data required:
Interval/ratio sometimes ordinal data.
At least two measures on each subjects at the
interval/ratio level.
Assumptions:
The sample must be representative of the population.
The variables that are being correlated must be normally
distributed.
The relationship between variables must be LINEAR.

7. Directions of Correlations on ScatterPlot
Positive Negative
No Correlation
Non-linear(Curvilinear(

8. 05/04/14 Dr Tarek Amin 8
Relationships Measured with Correlation Coefficient
The correlation coefficient is the cross products
of the Z-scores.
[ ]( )nzXzYr ∑=
Where:
ZX= the z-score of variable X
ZY= the z-score of variable Y
N= number of observations

9.  Because the means and standard deviations
of any given two sets of variables are
different, we cannot directly compare the
two scores.
 However, we can, transform them from the
ordinary absolute figures to Z-scores with a
mean of 0 and SDof 1.
 The correlation is the mean of the cross-
products of the Z-score foreach value
included, a measure of how much each pair
of observations (scores) varies together.
Tips

10. Correlation Coefficient (r)
The correlation coefficient r allows us to
state mathematically the relationship that
exists between two variables. The correlation
coefficient may range from +1.00 through 0.00 to – 1.00.
 A + 1.00 indicates a perfect positive
relationship,
 0.00 indicates no relationship,
 and -1.00 indicates a perfect negative
relationship.

11. I-Strength of the Correlation Coefficient
How large r should forit to be useful?
In decision making at least 0.95 while those concerning
human behaviors 0.5 is fair.
The strengths of r are as follow:
0.00-0.25 little if any.
0.26 -0.49 LOW
0.50- 0.69 Moderate
0.70 - 0.89 High
0.90 – 1.00 Very high .

12. II-Significance of the Correlation
The level of statistical significance is greatly
affected by the sample size n.
If r is based on a sample of 1,000, there is much
greaterlikelihood that it represents the r of the
population than if it were based on 10 subjects.

13. ‘ With large sample sizes rs that are described as
demonstrating (little if any) relationship are
statistically significant’
Statistical significance implies that r
did not occurby chance, the
relationship is greaterthan zero.

14. - The correlation coefficient also tell us the type
of relation that exists; that is, whetheris
positive ornegative.
- The relationship between job satisfaction and job
turnoverhas been shown to be negative; an
inverse relationship exists between them.
When one variable increases, the other decreases.
- Those with highergrades have lowerdropout rates
(a positive relationship).
Increases in the score of one variable is accompanied by
increase in the other.
III- Direction of correlation

15. Relationships Measured by Correlation
Coefficients:
When using the formula with Z-scores, ris the
average of the corss-products of the Z-scores.
[ ]( )nzXzYr ∑=
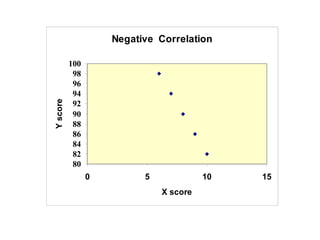
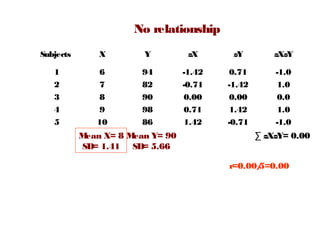
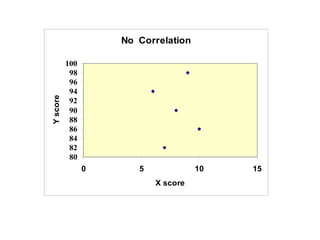
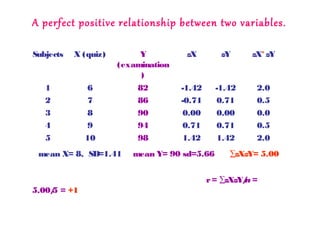
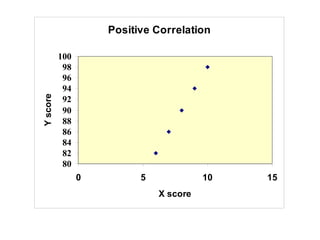
A five subjects took a quiz X, on which the scores ranged from
6to 10 and an examination Y, on which the scores ranged form
82to 98.
Calculate r and determine the pattern of correlation?

16. 05/04/14 Dr Tarek Amin 16
Formula forcalculating correlation coefficient r.
[ ]( )nzXzYr ∑=

17. A perfect positive relationship between two variables.
Subjects X (quiz) Y
(examination
)
zX zY zX*zY
1
2
3
4
5
6
7
8
9
10
82
86
90
94
98
-1.42
-0.71
0.00
0.71
1.42
-1.42
0.71
0.00
0.71
1.42
2.0
0.5
0.0
0.5
2.0
mean X= 8, SD=1.41 mean Y= 90 sd=5.66 ∑zXzY= 5.00
r= ∑zXzY/n =
5.00/5 = +1

18. Positive Correlation
80
82
84
86
88
90
92
94
96
98
100
0 5 10 15
X score
Yscore

19. Perfect negative relationship
Subjects X Y zX zY zXzY
1
2
3
4
5
6
7
8
9
10
98
94
90
86
82
-1.42
-0.71
00.0
0.71
1.42
1.42
0.71
0.00
-0.71
-1.42
-2.0
-0.5
0.0
-0.71
-2.0
Mean X =8
SD= 1.41
Mean Y= 90
SD= 5.66
zXzY= -5.00∑
[ ]( )nzXzYr ∑= - =5.0/5-=1.0

20. Negative Correlation
80
82
84
86
88
90
92
94
96
98
100
0 5 10 15
X score
Yscore

21. No relationship
Subjects X Y zX zY zXzY
1
2
3
4
5
6
7
8
9
10
94
82
90
98
86
-1.42
-0.71
0.00
0.71
1.42
0.71
-1.42
0.00
1.42
-0.71
-1.0
1.0
0.0
1.0
-1.0
Mean X= 8
SD= 1.41
Mean Y= 90
SD= 5.66
zXzY= 0.00∑
r=0.00/5=0.00

22. No Correlation
80
82
84
86
88
90
92
94
96
98
100
0 5 10 15
X score
Yscore

23. The following table is SPSS output describing the correlation between age, education in years,
smoking history, satisfaction with the current weight, and the overall state of health fora randomly
selected subjects.
Overall state
of health
Satisfaction
with current
weight
Smoking
history
Education in
years
Subject's
age
1.000
.
434
Subject's age
Pearson Correlation
Sig.(2 tailed)
N
.022
.649
419
Education in years
Pearson Correlation
Sig.(2 tailed)
N
-.108*
.026
423
.143**
.003
432
Smoking history
Pearson Correlation
Sig.(2 tailed)
N
-.009
.849
440
.033
.493
424
-.077
.109
432
Satisfaction with current
weight
Pearson Correlation
Sig.(2 tailed)
N
1.000
.
444
.370*
.000
443
-.200*
.000
441
.149**
.000
425
-.126**
.009
433
Overall state of health
Pearson Correlation
Sig.(2 tailed)
N
*Correlation is significant at the 0.05 level (2-tailed(.
** Correlation is significant at the 0.01 level (2-tailed).

24. Figure (1): Insulin resistance (HOMA-IR) in relation to
serum ferritin level among cases and controls.
Ferritin (log)
2.82.62.42.22.01.8
HOMA-RI
8
7
6
5
4
3
2
Controls
Sickle
Total Population
r=0.804, P=0.0001

25. Figure (2): 1,25 (OH) vitamin D in relation to body mass
index among obese and lean controls.
Body mass index
5040302010
VitaminDlevel
100
80
60
40
20
0
Lean
Obese
Total Population
r= -.166, P=0.036

26. 05/04/14 Dr Tarek Amin 26
Thank you