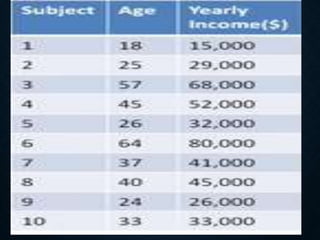
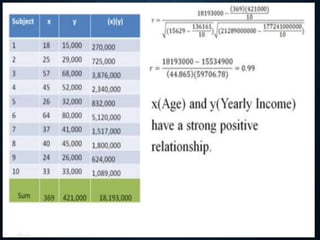
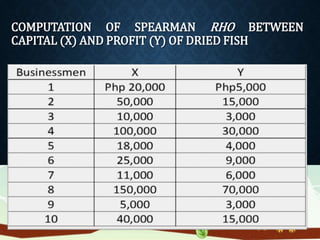
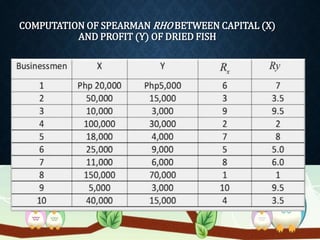
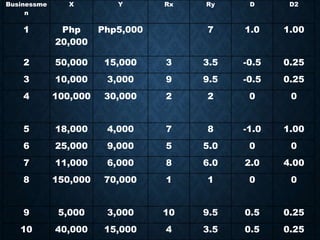
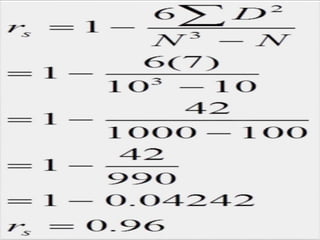Correlation analysis is used to determine the relationship between two or more variables. It can analyze the degree, direction, and type of relationship. The key types of correlation are positive (variables increase together), negative (variables change inversely), simple (two variables), partial (three+ variables with some held constant), and multiple (three+ variables together). Correlation can also be linear (constant ratio of changes) or non-linear (varying ratio of changes). It is useful for understanding variable behavior, estimating values, and interpreting results with measures like the correlation coefficient and coefficient of determination.

1. CORRELATION ANALYSIS

2. MEANING OF CORRELATION ANALYSIS
Correlation analysis is a process to find out the
degree of relationship between two or more
variables by applying various statistical tools and
techniques.
According to A.M. Tuttle
“Correlation is an analysis of the association between
two or more variable”

3. USES OF CORRELATION ANALYSIS
• It is used in deriving the degree and direction of
relationship within the variables.
• It is used in reducing the range of uncertainty in
matter of prediction.
• It I used in presenting the average relationship
between any two variables through a single value of
coefficient of correlation.

4. USES OF CORRELATION ANALYSIS
• In the field of science and philosophy these
methods are used for making progressive
conclusions.
• In the field of nature also, it is used in
observing the multiplicity of the inter related
forces.

5. Types of correlation
On the basis of
degree of
correlation
On the basis of
number of variables
On the basis of
linearity
•Positive
correlation
•Negative
correlation
•Simple correlation
•Partial correlation
•Multiple
correlation
•Linear
correlation
•Non – linear
correlation

6. CORRELATION : ON THE BASIS OF DEGREE
• Positive Correlation
if one variable is increasing and with its impact on
average other variable is also increasing that will be
positive correlation.
For example :
Income ( Rs.) : 350 360 370 380
Weight ( Kg.) : 30 40 50 60

7. •Negative correlation
if one variable is increasing and with its
impact on average other variable is also
decreasing that will be positive
correlation.
For example :
Income ( Rs.) : 350 360 370 380
Weight ( Kg.) : 80 70 60 50

8. CORRELATION : ON THE BASIS OF
NUMBER OF VARIABLES
• Simple correlation
Correlation is said to be simple when only two variables
are analyzed.
For example :
Correlation is said to be simple when it is done between
demand and supply or we can say income and
expenditure etc.

9. •Partial correlation :
When three or more variables are considered for
analysis but only two influencing variables are
studied and rest influencing variables are kept
constant.
For example :
Correlation analysis is done with demand, supply and
income. Where income is kept constant.

10. •Multiple correlation :
In case of multiple correlation three or more variables
are studied simultaneously.
For example :
Rainfall, production of rice and price of rice are studied
simultaneously will be known are multiple
correlation.

11. CORRELATION : ON THE BASIS OF
LINEARITY
• Linear correlation :
If the change in amount of one variable tends to make
changes in amount of other variable bearing constant
changing ratio it is said to be linear correlation.
For example :
Income ( Rs.) : 350 360 370 380
Weight ( Kg.) : 30 40 50 60

12. NON LINEAR CORRELATION
If The change in amount of one variable tends to make
changes in amount of other variable but not bearing
constant changing ratio it is said to be non - linear
correlation.
For example :
Income ( Rs.) : 320 360 410 490
Weight ( Kg.) : 21 33 49 56

13. IMPORTANCE OF CORRELATION
ANALYSIS :
• Measures the degree of relation i.e. whether it is positive
or negative.
• Estimating values of variables i.e. if variables are highly
correlated then we can find value of variable with the
help of gives value of variable.
• Helps in understanding economic behavior.

15. PEARSON r (CORRELATION)
•A linear correlation necessary to find the
degree of the association of two sets of
variables X and Y.

16. FORMULA:

20. PROBABLE ERROR :
Probable error determine the reliability of the value of the coefficient
in so far as it depends on the conditions of random sampling. It helps
in interpreting its value.
P.E.r = 0.6745 (1-r2)/√n
r = coefficient of correlation.
n = number of pairs of observation.

21. CONDITIONS UNDER PROBABLE ERROR :
 if the value of r is less than the probable error
there is no evidence of correlation, i.e. the value
of r is not at all significant.
If the value of r is more than six times the
probable error, the coefficient of correlation is
practically certain i.e. the value of r is significant.

22. CONDITIONS UNDER PROBABLE ERROR
• By adding and subtracting the value of
probable error from the coefficient of
correlation we get the upper and lower limits,
between correlation lies.
P = r+ P.E. ( upper limit )
P = r- P.E. ( lower limit )

23. COEFFICIENT OF DETERMINATION :
Coefficient of determination also helps in interpreting the value of
coefficient of correlation. Square of value of correlation
is used to find out the proportionate relationship or dependence of
dependent variable on independent variable. For e.g. r= 0.9 then r2 =
.81 or 81% dependence of dependent variable on independent variable.
Coefficient of Determination = Explained variation
Total variance

24. SPEARMAN RANK CORRELATION
A statistic which is used to measure the
relationship of paired ranks assigned to
individual scores on two variables.

25. FORMULA:

27. COMPUTATION OF SPEARMAN RHO BETWEEN
CAPITAL (X) AND PROFIT (Y) OF DRIED FISH

28. COMPUTATION OF SPEARMAN RHO BETWEEN CAPITAL (X)
AND PROFIT (Y) OF DRIED FISH

29. Businessme
n
X Y Rx Ry D D2
1 Php
20,000
Php5,000 7 1.0 1.00
2 50,000 15,000 3 3.5 -0.5 0.25
3 10,000 3,000 9 9.5 -0.5 0.25
4 100,000 30,000 2 2 0 0
5 18,000 4,000 7 8 -1.0 1.00
6 25,000 9,000 5 5.0 0 0
7 11,000 6,000 8 6.0 2.0 4.00
8 150,000 70,000 1 1 0 0
9 5,000 3,000 10 9.5 0.5 0.25
10 40,000 15,000 4 3.5 0.5 0.25

31. THANK
YOU

32. REFERENCES :
• S. P. Gupta
• S. C. Gupta
• www.wikipedia.org
• Mr. Kohli
• Mr. D. Patri