Download as PPS, PPTX
Uploaded byKhalid Aziz
Correlation and regression
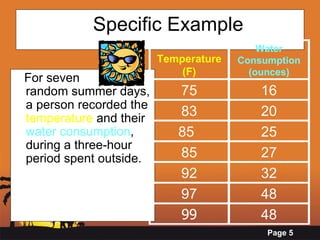
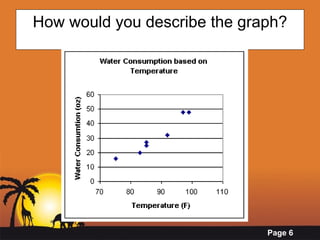
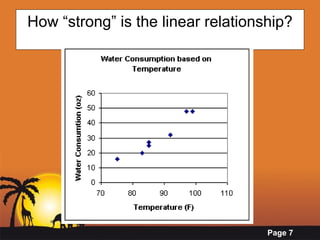
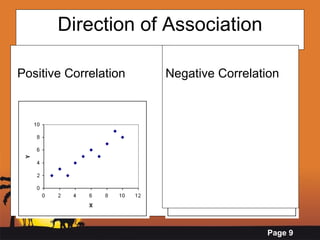
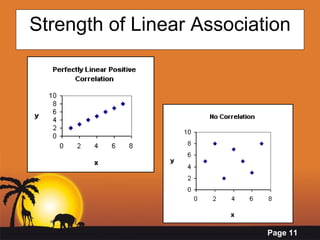
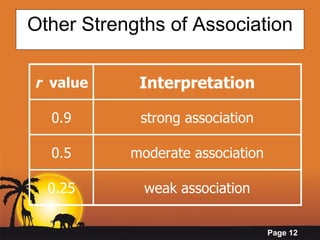
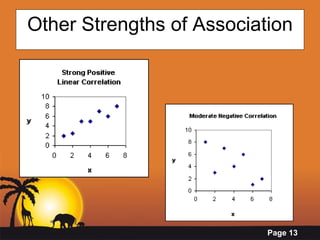
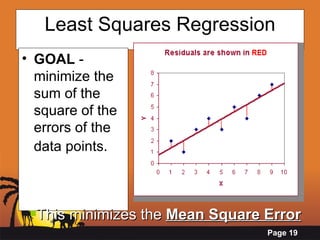
This document provides an introduction to correlation and regression analysis. It defines correlation as a measure of the association between two variables and regression as using one variable to predict another. The key aspects covered are: - Calculating correlation using Pearson's correlation coefficient r to measure the strength and direction of association between variables. - Performing simple linear regression to find the "line of best fit" to predict a dependent variable from an independent variable. - Using a TI-83 calculator to graphically display scatter plots of data and calculate the regression equation and correlation coefficient.
More Related Content
Similar to Correlation and regression
Correlation and regression
- 1. Introduction to Correlationand Regression ECONOMICS OF ICMAP, ICAP, MA-ECONOMICS, B.COM. FINANCIAL ACCOUNTING OF ICMAP STAGE 1,3,4 ICAP MODULE B, B.COM, BBA, MBA & PIPFA. COST ACCOUNTING OF ICMAP STAGE 2,3 ICAP MODULE D, BBA, MBA & PIPFA. CONTACT: KHALID AZIZ 0322-3385752 R-1173,ALNOOR SOCIETY, BLOCK 19,F.B.AREA, KARACHI, PAKISTAN
- 2. Outline Introduction Linear Correlation Regression Simple Linear Regression Using the TI-83 Model/Formulas
- 3. Outline continued ApplicationsReal-life Applications Practice Problems Internet Resources Applets Data Sources
- 4. Correlation Correlation A measure of association between two numerical variables. Example (positive correlation) Typically, in the summer as the temperature increases people are thirstier.
- 5. Specific Example For seven random summer days, a person recorded the temperature and their water consumption , during a three-hour period spent outside. Temperature (F) Water Consumption (ounces) 75 16 83 20 85 25 85 27 92 32 97 48 99 48
- 6. How would youdescribe the graph?
- 7. How “strong” isthe linear relationship?
- 8. Measuring the RelationshipPearson’s Sample Correlation Coefficient, r measures the direction and the strength of the linear association between two numerical paired variables.
- 9. Direction of AssociationPositive Correlation Negative Correlation
- 10. Strength of LinearAssociation r value Interpretation 1 perfect positive linear relationship 0 no linear relationship -1 perfect negative linear relationship
- 11. Strength of LinearAssociation
- 12. Other Strengths ofAssociation r value Interpretation 0.9 strong association 0.5 moderate association 0.25 weak association
- 13. Other Strengths ofAssociation
- 14. Formula = the sum n = number of paired items x i = input variable y i = output variable x = x-bar = mean of x ’s y = y-bar = mean of y ’s s x = standard deviation of x ’s s y = standard deviation of y ’s
- 15. Regression Regression Specificstatistical methods for finding the “line of best fit” for one response (dependent) numerical variable based on one or more explanatory (independent) variables.
- 16. Curve Fitting vs.Regression Regression Includes using statistical methods to assess the "goodness of fit" of the model. (ex. Correlation Coefficient)
- 17. Regression: 3Main Purposes To describe (or model) To predict ( or estimate) To control (or administer)
- 18. Simple Linear RegressionStatistical method for finding the “line of best fit” for one response (dependent) numerical variable based on one explanatory (independent) variable.
- 19. Least Squares RegressionGOAL - minimize the sum of the square of the errors of the data points. This minimizes the Mean Square Error
- 20. Example Plan anoutdoor party. Estimate number of soft drinks to buy per person, based on how hot the weather is. Use Temperature/Water data and regression .
- 21. Steps to Reachinga Solution Draw a scatterplot of the data.
- 22. Steps to Reachinga Solution Draw a scatterplot of the data. Visually, consider the strength of the linear relationship.
- 23. Steps to Reachinga Solution Draw a scatterplot of the data. Visually, consider the strength of the linear relationship. If the relationship appears relatively strong, find the correlation coefficient as a numerical verification.
- 24. Steps to Reachinga Solution Draw a scatterplot of the data. Visually, consider the strength of the linear relationship. If the relationship appears relatively strong, find the correlation coefficient as a numerical verification. If the correlation is still relatively strong, then find the simple linear regression line.
- 25. Our Next StepsLearn to Use the TI-83 for Correlation and Regression. Interpret the Results (in the Context of the Problem).
- 26. Finding the Solution: TI-83 Using the TI- 83 graphing calculator Turn on the calculator diagnostics. Enter the data. Graph a scatterplot of the data. Find the equation of the regression line and the correlation coefficient. Graph the regression line on a graph with the scatterplot.
- 27. Preliminary Step Turnthe Diagnostics On. Press 2nd 0 (for Catalog). Scroll down to DiagnosticOn . The marker points to the right of the words. Press ENTER . Press ENTER again. The word Done should appear on the right hand side of the screen.
- 28. Example Temperature (F)Water Consumption (ounces) 75 16 83 20 85 25 85 27 92 32 97 48 99 48
- 29. 1. Enterthe Data into Lists Press STAT . Under EDIT , select 1: Edit . Enter x-values (input) into L1 Enter y-values (output) into L2 . After data is entered in the lists, go to 2nd MODE to quit and return to the home screen. Note: If you need to clear out a list, for example list 1, place the cursor on L1 then hit CLEAR and ENTER .
- 30. 2. Set upthe Scatterplot. Press 2nd Y= (STAT PLOTS). Select 1: PLOT 1 and hit ENTER . Use the arrow keys to move the cursor down to On and hit ENTER . Arrow down to Type: and select the first graph under Type. Under Xlist: Enter L1 . Under Ylist: Enter L2 . Under Mark: select any of these.
- 31. 3. View theScatterplot Press 2nd MODE to quit and return to the home screen. To plot the points, press ZOOM and select 9: ZoomStat . The scatterplot will then be graphed.
- 32. 4. Find theregression line. Press STAT . Press CALC . Select 4: LinReg(ax + b) . Press 2nd 1 (for List 1) Press the comma key , Press 2nd 2 (for List 2) Press ENTER .
- 33. 5. Interpretingand Visualizing Interpreting the result: y = ax + b The value of a is the slope The value of b is the y-intercept r is the correlation coefficient r 2 is the coefficient of determination
- 34. 5. Interpretingand Visualizing Write down the equation of the line in slope intercept form. Press Y= and enter the equation under Y1. (Clear all other equations.) Press GRAPH and the line will be graphed through the data points.
- 35.
- 36. Interpretation in ContextRegression Equation: y=1.5*x - 96.9 Water Consumption = 1.5*Temperature - 96.9
- 37. Interpretation in ContextSlope = 1.5 (ounces)/(degrees F) for each 1 degree F increase in temperature, you expect an increase of 1.5 ounces of water drank.
- 38. Interpretation in Contexty-intercept = -96.9 For this example, when the temperature is 0 degrees F, then a person would drink about -97 ounces of water. That does not make any sense! Our model is not applicable for x=0.
- 39. Prediction Example Predict the amount of water a person would drink when the temperature is 95 degrees F. Solution: Substitute the value of x=95 (degrees F) into the regression equation and solve for y (water consumption). If x=95, y=1.5*95 - 96.9 = 45.6 ounces.
- 40. Strength of theAssociation: r 2 Coefficient of Determination – r 2 General Interpretation: The coefficient of determination tells the percent of the variation in the response variable that is explained (determined) by the model and the explanatory variable.
- 41. Interpretation of r 2 Example: r 2 =92.7%. Interpretation: Almost 93% of the variability in the amount of water consumed is explained by outside temperature using this model. Note: Therefore 7% of the variation in the amount of water consumed is not explained by this model using temperature.
- 42.
- 43. Simple Linear RegressionModel The model for simple linear regression is There are mathematical assumptions behind the concepts that we are covering today.
- 44.
- 45. Real Life ApplicationsCost Estimating for Future Space Flight Vehicles (Multiple Regression)
- 46. Nonlinear Application Predictingwhen Solar Maximum Will Occur http://science.msfc.nasa.gov/ssl/pad/ solar/predict.htm
- 47. Real Life ApplicationsEstimating Seasonal Sales for Department Stores (Periodic)
- 48. Real Life ApplicationsPredicting Student Grades Based on Time Spent Studying
- 49. Real Life Applications. . . What ideas can you think of? What ideas can you think of that your students will relate to?
- 50. Practice Problems MeasureHeight vs. Arm Span Find line of best fit for height. Predict height for one student not in data set. Check predictability of model.
- 51. Practice Problems Isthere any correlation between shoe size and height? Does gender make a difference in this analysis?
- 52. Practice Problems Canthe number of points scored in a basketball game be predicted by The time a player plays in the game? By the player’s height? Idea modified from Steven King, Aiken, SC. NCTM presentation 1997.)
- 53. JOIN KHALID AZIZECONOMICS OF ICMAP, ICAP, MA-ECONOMICS, B.COM. FINANCIAL ACCOUNTING OF ICMAP STAGE 1,3,4 ICAP MODULE B, B.COM, BBA, MBA & PIPFA. COST ACCOUNTING OF ICMAP STAGE 2,3 ICAP MODULE D, BBA, MBA & PIPFA. CONTACT: 0322-3385752 0312-2302870 0300-2540827 R-1173,ALNOOR SOCIETY, BLOCK 19,F.B.AREA, KARACHI, PAKISTAN
Editor's Notes
- #5 Typically, in the summer as the temperature increases people are thirstier. Consider the two numerical variables, temperature and water consumption. We would expect the higher the temperature, the more water a given person would consume. Thus we would say that in the summer time, temperature and water consumption are positively correlated.
- #6 (The data is shown in the table with the temperature placed in increasing order.)
- #7 This graph helps us visualize what appears to be a somewhat linear relationship between temperature and the amount of water one drinks.
- #10 Direction of the Association: The association can be either positive or negative. Positive Correlation: as the x variable increases so does the y variable. Example: In the summer, as the temperature increases, so does thirst. Negative Correlation: as the x variable increases, the y variable decreases. Example: As the price of an item increases, the number of items sold decreases.
- #11 Strength of the Association: The strength of the linear association is measured by the sample Correlation Coefficient, r. r can be any value from –1 to +1. The closer r is to one (in magnitude) the stronger the linear association. If r equals zero, then there is no linear association between the two variables.
- #13 * No other values of r have precise definitions of strength. See the chart below. Note: All of the values in the second table are positive. Thus the associations are positive. The same strength interpretations hold for negative values of r, only the direction interpretations of the association would change.
- #18 To describe or model a set of data with one dependent variable and one (or more) independent variables. To predict or estimate the values of the dependent variable based on given value(s) of the independent variable(s). To control or administer standards from a useable statistical relationship.
- #19 Simple: only one independent variable Linear in the Independent Variable: the independent variable only appears to the first power.
- #20 Regression analysis tries to fit a model to one response variable based on one or more explanatory variables. In most cases, there will be error. See the graph below for an example of Simple Linear Regression. The actual data points (x,y) are the blue dots The Least Squares linear model (regression line) of the response (y) variable based on the the explanatory (x) variable is shown in black. The errors (residuals) for each data point to its predicted value are the vertical lines shown in red. The goal, in general, is to minimize the errors from the actual data to the regression line. The least squares line minimizes the sum of the square of the errors.
- #21 If you were planning an outdoor party in the summer time, you might need to estimate how many soft drinks to buy. In your planning, you will, of course, need to know how many people will be attending. However, as you determine the number of soft drinks for each person, you might want to also consider how hot it will be. The temperatures have been forecasted for around 95 degrees on the day of the outdoor party. (In real life, you would probably make an estimate based on your previous experience and make a logical increase based on the temperature.) We will use some hypothetical data to determine how thirsty people might be. We will use the Temperature/Water example data for this.
- #39 And we cannot expect it be accurate at such low temperatures, because the sample of data was taken in the summer time and the temperatures range from 75 to 99 degrees Fahrenheit. Thus the model only predicts for temperatures in approximately that range.
- #40 Solution: Substitute the value of x=95 (degrees F) into the regression equation y=1.5*x - 96.9 and solve for y (water consumption). y=1.5*x - 96.9 if x=95, then y=1.5*95 - 96.9 = 45.6 ounces. Note: Since 95 degrees F is in the range of values that were used to find the regression equation, then we can use this equation to predict the water consumption. If the desired prediction had been for 50 degrees F, then the model should not be used, since the value of x does not fall in the range of predictability for this model.
- #42 Note: This means that approximately 7% of the variation in the water consumption is not explained by the temperature. So perhaps there is another variable that accounts for the remaining portion of the variation. Can you think of a reasonable variable? Multiple Regression is the name of the method that would include more than one independent variable to predict amount of water people would drink.
- #47 Predicting the Solar MaximumPlanning for satellite orbits and space missions often require advance knowledge of solar activity levels. NASA scientists are using new techniques to predict sunspot maxima years in advance. Click here for the latest predictions for the current solar cycle. Click on the image for current predictions
- #51 Compare the height and arm span of students in the class, except for one student. Test for the strength of association between the two variables. Measure the arm span of the one student and ask the class to predict the student's height.
- #53 Have students search the Internet or other sources for data on basketball players. In particular, find the number of points scored in a game and the number of minutes played in that same game. Based on the data, could the number of points scored in a game be predicted by the amount of time a player plays in a game? Have students suggest alternative ways to set up the situation that would provide better prediction capabilities and ask them to find the data to check their theories. (Idea modified from Steven King, Aiken, SC. NCTM presentation 1997.)