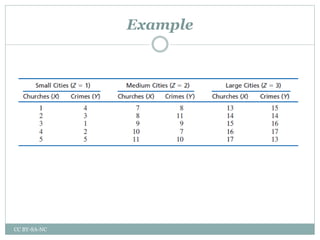
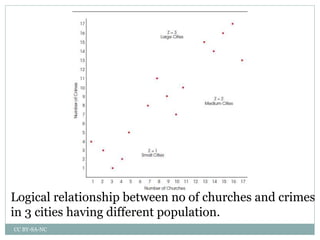
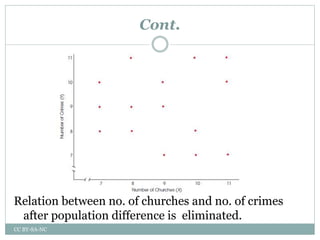
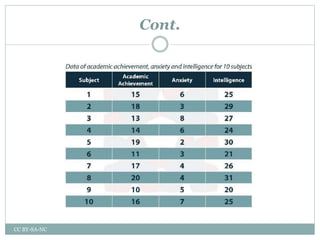
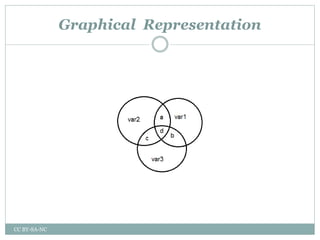
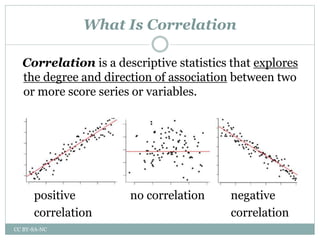
This document is a presentation by Dwaiti Roy on partial correlation. It begins with an acknowledgement section thanking various professors and resources that helped in preparing the presentation. It then provides definitions and explanations of key concepts related to partial correlation such as correlation, assumptions of correlation, coefficient of correlation, coefficient of determination, variates, partial correlation, assumptions and hypothesis of partial correlation, order and formula of partial correlation. Examples are provided to illustrate partial correlation. The document concludes with references and suggestions for further reading.

1. NAME: DWAITI ROY
APPLICATION NO:
8536ae51e72f11e9a93cbd5fd00aa9e7
AFFILIATION: Banaras Hindu University
Partial Correlation
CC BY-SA-NC

2. ACKNOWLEDGEMENT
Course Name: Academic Writing
First of all, I would like to thank Dr. Ajay Semalty and
the full team of AW to deliver such a rich content
regarding academic writing. It helped a lot in making
this presentation. Secondly I’m thankful to all my
professors who helped me in preparing the
presentation. Lastly I am grateful to the books,
without which the presentation would have been
incomplete.
CC BY-SA-NC

3. What Is Correlation
Correlation is a descriptive statistics that explores
the degree and direction of association between two
or more score series or variables.
positive no correlation negative
correlation correlation
CC BY-SA-NC

4. Assumptions Of Correlation
 It cannot be generalized beyond the sample or
population from where the data belongs.
 It may not indicate any cause and effect relationship
between two or more variables.
 Correlation cannot predict the value from one
variable from that of another.
 The variables involved in the correlation are random
variables, and cannot be manipulated by the
researcher.
CC BY-SA-NC

5. Coefficient Of Correlation
The coefficient of correlation is the ratio which
expresses the extent to with changes to one variable
are accompanied by the changes of another variable.
Generally the coefficient of correlation is measured
by Pearson Product Moment Correlation, denoted
by ‘r’.
CC BY-SA-NC

6. Cont.
The general formula for computing product-moment
correlation is –
where,
r = product moment coefficient of correlation,
N = total no of paired scores,
 
  



])(][)([ 2222
YYNXXN
YXXYN
r
CC BY-SA-NC

7. Cont.
X = the first variable,
Y = the second variable.
Thus when r is said to be +0.07 that implies two
thing – the sign implies the direction of relationship,
i.e. if variable X increase variable Y will also
increases. And the magnitude implies the strength of
relationship.
CC BY-SA-NC

8. Coefficient Of Determination
Coefficient of determination (r2) is the
technique of measuring the strength of variable. It
measures how much of the variability in one variable
is predictable from its relationship with the other
variable.
For e.g. - a correlation of r = 0.80 would mean that
r2 = 0.64 (or 64%) of the variance in criterion
variable can be predicted from relation with the
predictor variable.
CC BY-SA-NC

9. Concept of Variate
Variate is the weighted composite of two or more
directly observable variables that are combined
linearly. Thus a statistic may contain one variate
(known as univariate statistics, e.g. t-test), two
variates (known as bivatiate statistics, e.g.
product-moment correlation) or more than two
variates (known as multivariate statistics, e.g.
multiple regression analysis).
CC BY-SA-NC

10. Partial Correlation
 Special form of correlation between two variables.
 Part of multivariate statistics involving more than
two variables in a sample.
 Aims at eliminating effects of other variable on both
the variables in common.
 It is the part of product moment r between two given
variable that is remained after elimination of
components of their association, arising from other
variables on both of them.
CC BY-SA-NC

11. Assumptions Of Partial Correlation
 All the variables involved are continuous
measurement variable.
 Scores of variables have unimodal or fairly
symmetrical distribution without any marked
skewness.
 The paired scores of each pair of variables are
independent of all other scores in the sample.
 There is a linear association between the scores of
every pair.
CC BY-SA-NC

12. Order Of Partial Correlation
 There are different orders of partial correlation
depending on the number of variables to be
eliminated.
 If there is no elimination of other variables is to be
known as zero order r, indicated as r12.
 If there is elimination of one variable from the other
variables is to be known as first order partial r,
indicated as r12.3.
 If there is four inter connected variables and two are
to eliminate from others is to be known as second
order partial r, indicated as r12.34.
CC BY-SA-NC

13. Hypothesis For Partial Correlation
 Null hypothesis : There is no partial correlation
between variables or the partial correlation is zero
and partial r resulted only due to chance.
 Alternate hypothesis : There is partial
correlation between variables or the partial
correlation is not zero.
CC BY-SA-NC

14. The Formula of Partial Correlation
 The first order partial correlation is used to define the
process.
 The formula for computing partial correlation is
Where, r12 = correlation coefficient of variable 1 and 2
r 13 = correlation coefficient of variable 1 and 3
r23 = correlation coefficient of variable 2 and 3
2
23
2
13
231312
3.12
11 rr
rrr
r



CC BY-SA-NC

15. Example
CC BY-SA-NC

16. Cont.
The hypothetical scores have been constructed to
simulate the church/crime/population situation for a
sample of n = 15 cities.
 The X variable represents the number of churches,
 Y represents the number of crimes, and
 Z represents the population for each city.
 The cities are grouped into three categories based on
population (small cities, medium cities, large cities)
with n = 5 cities in each group.
CC BY-SA-NC

17. Cont.
Here it is seen that as the population increases from on
city to another, the number of churches and crimes
also increase.
Here, rXY = .923
rXZ = .961
rYZ = .961
Partial r allows to hold the population constant and
see the underlying effect of churches and crimes.
CC BY-SA-NC

18. Logical relationship between no of churches and crimes
in 3 cities having different population.
CC BY-SA-NC

19. Cont.
The computed partial r is 0 in the above case. Thus it
can be said that when the population difference is
eliminated there is no correlation between churches
and crime.
CC BY-SA-NC

20. Cont.
Relation between no. of churches and no. of crimes
after population difference is eliminated.
CC BY-SA-NC

21. Another Example
Researcher wants to compute correlation between
anxiety and achievement controlled from
intelligence. If anxiety denote ‘X’, achievement
denote ‘Y’ and intelligence denote ‘Z’ then correlation
coefficient will be rXY.Z .
CC BY-SA-NC

22. Cont.
CC BY-SA-NC

23. Cont.
 rXY = -.369
 rYZ = -.245
 rXZ = .918
 And computed rXY.Z = -.375
The partial correlation is negative. Thus in the above
example, if the factor intelligence is eliminated then
achievement increases with the decrease in anxiety.
CC BY-SA-NC

24. Checking Significance
 To check significance partial r is transformed into t
score and compared with critical t scores.
 Formula for transforming to t score is
 Where rp = partial r
n = sample size
v = total number of variable
2
1 p
p
r
vnr
t



CC BY-SA-NC

25. Cont.
Thus for above e.g. t score for partial r is 1.69 which
found not to be significant at 0.05 or 0.01 level
against df (n-v) = 7.
CC BY-SA-NC

26. Graphical Representation
CC BY-SA-NC

27. Cont.
 Here, ‘a’ = variance shared by variable 1 and 2
 ‘b’ = variance shared by variable 1 and 3
 ‘c’ = variance shared by variable 2 and 3 and
 ‘d’ = common variance shared by both variable 1,2
and 3.
Thus partial r is the variance shared by variable
1 and 2 , that is devoid of any variance
explained by variable 3.
CC BY-SA-NC

28. References
1. Das, D., & Das, A.(2017). Statistics In Biology And
Psychology(6th ed.). pg. 162-164. Kolkata:
Academic Publisher.
2. Gravetter, F.J., Wallnau, L.B.(2015). Statistics For
The Behavioural Sciences(10th ed.). pg. 502-505.
Boston: Cengage Learning.
CC BY-SA-NC

29. Further Reading
 Gravetter, F.J., Wallnau, L.B.(2015). Statistics For
The Behavioural Sciences(10th ed.).
 Heiman, G.W.,(2011). Basic Statistics for the
Behavioural Sciences(6th ed.).
 Tabachnick, B.G., Fidell, L.S.,(2013). Using
Multivariate Statistics(6th ed.).
CC BY-SA-NC

30. Feedback Of The Course
Application Number:
8536ae51e72f11e9a93cbd5fd00aa9e7
The expectation from the course academic learning was
very high including to learn about various scopes of
academic learning. It met the expectation beautifully. I
appreciate the time to time lectures and the self
assessment quizzes in every week, which resulted in
better understanding of the topic. The additional gain
from the course was the knowledge about various OERs.
I would like to thank Dr. Ajay Semalty as well as the
whole team of AW for arranging such a cohesive course
in such a comprehensive manner.
CC BY-SA-NC

31. THANK YOU.
CC BY-SA-NC