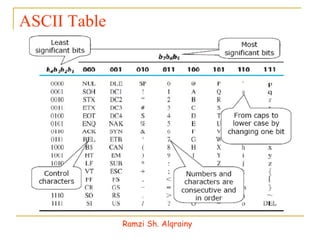
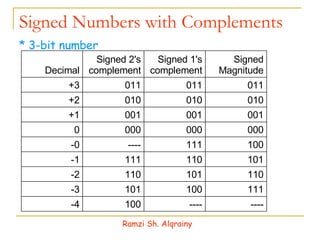
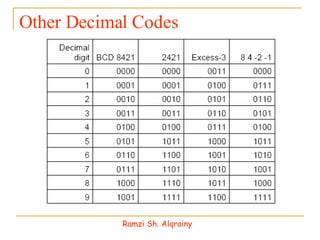
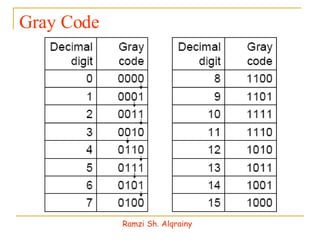
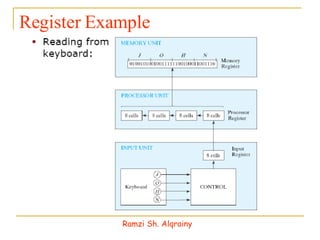
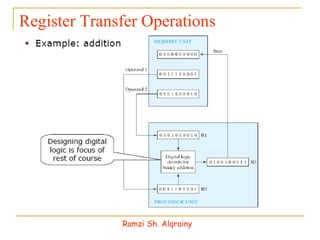
- Digital systems operate on discrete elements of information such as numbers, letters, and pictures by quantizing (digitizing) continuous data. - Numbers in digital systems are represented using strings of digits in different bases, with each digit position having an associated weight. Common number bases include binary, octal, decimal, and hexadecimal. - Information in digital systems is stored and processed using registers that are groups of binary cells (bits).

1. Digital Logic

2. Digital Systems * Digital systems operate on discrete elements of information # Numbers (e.g., pocket calculator) # Letters (e.g., word processor) # Pictures (e.g., digital cameras) * For a digital systems to operate on a continuous data, it needs to quantize (digitize) that data first # Covert data into digital representation * Digital systems # Cell phone # MP3 music player …. etc # digital camera Ramzi Sh. Alqrainy

3. Numbers Each number is represented by a string of digits , in which the position of each digit has an associated weight . Example: * In general , any decimal number D of the form Has the value Ramzi Sh. Alqrainy

6. * What is the range of values of an n -bit number in radix r ? # Minimum value: 0 # Maximum value: r n -1 # Number of different values: r n What is the range of values of an 4 -bit binary number? # Minimum value: 0 # Maximum value: 2 4 -1=15 # Number of different values: 2 4 = 16 ------------------------------------------------------------------------------- What is the range of values of an 2 -bit decimal number? # Minimum value: 0 # Maximum value: 10 2 -1=99 # Number of different values: 10 2 = 100 Ramzi Sh. Alqrainy

9. Number Base Conversions * Binary to octal conversion Starting at the binary point and working left, separate the bits into groups of three and replace each group with the corresponding octal digit. (1010011100) 2 =001 010 011 100=(1234) 8 * Binary to hexadecimal separate the bits into groups of four and replace each group with the corresponding hexadecimal digit. (1010011100) 2 = 0010 0100 1100 = (29C) 16 Ramzi Sh. Alqrainy

10. * Conversion of fractions Starting at the binary point , group the binary digits that lie to the right into groups of three or four. (0.10111) 2 = 0.101 110 = (0.56) 8 (0.10111) 2 = 0.1011 1000 = (0. B6) 16 * Conversion to binary numbers Replace each octal or hexadecimal digit with the corresponding 3 or 4 bit binary string (2414) 10 =(100101101110) 2 Ramzi Sh. Alqrainy ( 4 5 5 6 ) 8 ( 9 6 E ) 16

14. COMPLEMENT * Complement are used in digital computer for simplifying the subtraction operation. * There are two types of complement for each base-r system: 1- Diminished Radix Complement (r-1)’s 2- Radix Complement r’s # the two types are referred to as the 2’s complement and 1’s complement for binary number. # 10’s complement and 9’s complement for decimal number. Ramzi Sh. Alqrainy

16. Observation: * Subtraction from ( r n –1) will never require a borrow * Diminished radix complement can be computed digit-by-digit * For binary: 1 – 0 = 1 and 1 – 1 = 0 Ex . The 1’s complement of 1011000 is 0100111 The 1’s complement of 0101101 is 1010010 Ramzi Sh. Alqrainy The 1’s complement of a binary number is formed by changing 1’s to 0’s and 0’s to 1’s

22. Signed Numbers with Complements * 3-bit number Ramzi Sh. Alqrainy ---- ---- 100 -4 111 100 101 -3 110 101 110 -2 101 110 111 -1 100 111 ---- -0 000 000 000 0 001 001 001 +1 010 010 010 +2 011 011 011 +3 Signed Magnitude Signed 1's complement Signed 2's complement Decimal

23. Signed Numbers How are signed numbers handled in base 10? ~ Plus or minus sign placed in front of number Can we do that for binary numbers? ~ Sign needs to be represented in digital system ~ Only choice are ‘0’ and ‘1’ # ‘0’ indicates ‘+’ # ‘1’ indicates ‘–’ Examples on five-bit numbers: 01101 11101 00000 10000 + 13 – 13 + 0 – 0 Ramzi Sh. Alqrainy

26. BCD Addition Addition is done BCD digit by BCD digit ~ 4 bits at the time Can we use normal binary addition? * Problem : digits adding up to more than 9 ~ Binary addition will result in invalid BCD codes ~ 1010 … 1111 are not valid * Solution: check if resulting value is greater than 9 ~ if so, add 6 ~ 6 will offset the invalid BCD codes and generate the carry Ramzi Sh. Alqrainy

27. BCD Addition Example: 184 + 576 BCD carry 1 1 0001 1000 0100 184 + 0101 0111 0110 +576 Binary sum 0111 10000 1010 Add 6 0110 0110 BCD sum 0111 0110 0000 760 Ramzi Sh. Alqrainy

28. Decimal Arithmetic Everything needs to be 4-bit aligned 􀁹 ‘ +’ represented by 0 (=‘0000’) 􀁹 ‘–’ represented by 9 (=‘1001’) 􀂃 Signed magnitude representation or complements 􀁹 Signed magnitude hardly use 􀁹 10’s complement most common 􀂃 Example: 375 + (–240) 􀁹 Negative numbers represented by 10’s complement 􀁹 10’s complement of 240 is 104 – 240 = 9760 􀁹 Addition of all digits and discard of end carry: 0 375 + 9 760 0 130 􀁹 Sign of result automatically correct Ramzi Sh. Alqrainy

29. Other Decimal Codes Decimals can be encoded in many ways in 4 bits 􀂃 Weighted codes * Each bit position is assigned a weighting factor * Value of code is sum of weights where bits are ‘1’ * Is BCD a weighted code? » Yes! It’s a 8,4,2,1 code 􀁹 Other weighted code: » 2,4,2,1 code (yields non-unique coding) » 8,4,-2,-1 code 􀂃 Self-complementing codes * 9’s complement by exchanging 1’s with 0’s and 0’s with 1’s * Excess-3 and 2421 codes are self-complementing Ramzi Sh. Alqrainy

30. Other Decimal Codes Ramzi Sh. Alqrainy

31. Gray Code * Imaging you code a 2-bit number with two light switches connected to light bulbs ~ Can you count binary without causing ambiguity? * Probably not: ~ Switching from 01 to 10 cannot be done simultaneously on both bits # Either 01->00->10 or 01->11->10 * This brief error or ambiguity can cause problems * Gray code changes only one bit between consecutive numbers Ramzi Sh. Alqrainy

32. Gray Code Ramzi Sh. Alqrainy

34. ASCII Table Ramzi Sh. Alqrainy

35. Error-Detecting Code *Communication between systems can be “noisy” 􀁹 Environmental conditions can cause bit flips * Error-detecting code 􀁹 If one bit is flipped, the code becomes invalid 􀁹 Communication system can detect that and retransmit “ Parity bit ” is an extra bit included with a message to make the total number of 1’s either even or odd . 􀁹 “ Even parity”: choose parity bit such that # of 1’s is even 􀁹 “ Odd parity”: choose parity bit such that # of 1’s is odd * Example: 􀁹 Data=1000001, even parity=0, odd parity=1 􀁹 Data=1010100, even parity=1, odd parity=0 * Only one parity bit is used Ramzi Sh. Alqrainy

36. Binary Storage and Registers * How is information stored on a digital system? 􀁹 Bits are stored in “binary cells” 􀁹 Binary cell can have two stable states: ‘0’ and ‘1’ * Binary cells are grouped into registers 􀁹 n cells make up n-bit register * Size of registers is typically predefined 􀁹 Simple microcontroller: 8 bits = 1 byte 􀁹 Pentium: 32 bits = 4 bytes 􀁹 Mac G5: 64 bits = 8 bytes * Digital system can usually process entire registers 􀁹 “ Register transfer” operation specify processing Ramzi Sh. Alqrainy

37. Register Example Ramzi Sh. Alqrainy

38. Register Transfer Operations Ramzi Sh. Alqrainy