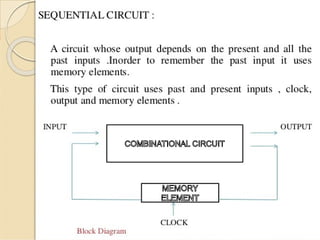
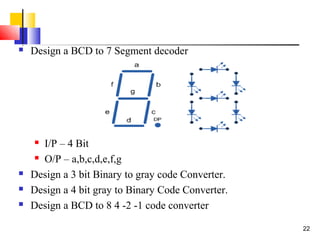
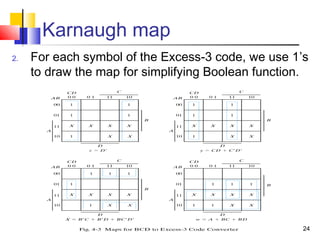
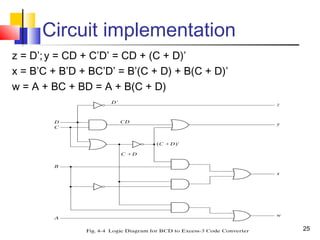
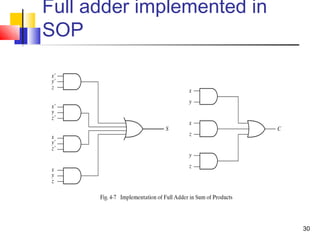
The document discusses combinational logic circuits. It covers sum-of-products and product-of-sums forms for representing logic functions. Methods for analyzing and simplifying logic circuits are presented, including Boolean algebra, Karnaugh maps, and deriving truth tables from logic diagrams. Examples of common logic circuits like adders, decoders, and converters are provided along with steps for designing combinational logic circuits.

1. 1

2. 2
Combinational Logic

3. 3

4. 4

5. 5

6. 6

7. Sum-of-Products Form
 Sum  OR
 Product  AND
 Each of the sum-of-products expression consists of two or more
AND terms that are ORed together.
 Examples: ABC+A’BC’
AB+A’BC’+C’D’+D
 Note that one inversion sign cannot cover more than one variable
in a term. AB is not allowed.

8. Product-of-Sums Form
 Each of the product-of-sums expression consists of two or more
OR terms that are ANDed together.
 Examples: (A+B’+C)(A+C)
(A+B’)(C’+D)F
 Will use sum-of-products form in logic circuit simplification.

9. Simplifying Logic Circuits

10. Example 4.1

11. Circuit Simplification Methods
 Boolean algebra: greatly depends on inspiration and
experience.
 Karnaugh map: systematic, step-by-step approach.
 Pros and Cons

12. Algebraic Simplification
 Use the Boolean algebra theorems introduced in Chapter 3 to help
simplify the expression for a logic circuit.
 Based on experience, often becomes a trial-and-error process.
 No easy way to tell whether a simplified expression is in its
simplest form.

13. Designing Combinational Logic Circuits
1. Set up the truth table.
2. Write the AND term for each case where the output is a 1.
3. Write the sum-of-products expression for the output.
4. Simplify the output expression.
5. Implement the circuit for the final expression.

14. Example
 Design a logic circuit that is to produce a HIGH output when the
voltage (represented by a four-bit binary number ABCD) is
greater than 6V.

15. Example
 Generate the STOP signal and energize an indicator light
whenever either of the following conditions exists: (1) there is no
paper in the paper feeder tray; or (2) the two micro-switches in the
paper path are activated, indicating a jam.

16. Karnaugh Map Method
 A graphical device to simplify a logic expression.
 Will only work on examples with up to 4 input variables.
 From truth table to logic expression to K map.
 K map with 2,3 and 4 variables.

17. Looping
 The expression for output X can be simplified by properly
combining those squares in the K map which contain 1s. The
process of combining these 1s is called looping.
 Looping groups of two (pairs)  eliminate 1 variable
 Looping groups of four (quads)  eliminate 2 variables
 Looping groups of eight (octets) eliminate 3 variables

18. 18
Analysis procedure
 To obtain the output Boolean functions from a logic diagram,
proceed as follows:
 Label all gate outputs that are a function of input variables with
arbitrary symbols. Determine the Boolean functions for each
gate output.
 Label the gates that are a function of input variables and
previously labeled gates with other arbitrary symbols. Find the
Boolean functions for these gates.
 Repeat the process outlined in step 2 until the outputs of the
circuit are obtained.
 By repeated substitution of previously defined functions,
obtain the output Boolean functions in terms of input variables.

19. 19
Example
F2 = AB + AC + BC; T1 = A + B + C; T2 = ABC; T3 = F2’T1;
F1 = T3 + T2
F1 = T3 + T2 = F2’T1 + ABC = A’BC’ + A’B’C + AB’C’ + ABC

20. 20
Derive truth table from logic diagram

21. Examples
 Design a combinational circuit with 3 inputs and one output.
The output is 1 if the binary value is of the input is less than 3,
Zero otherwise.
 Steps: TT, K Map, Logic Circuit
 Design a 3 I/P majority circuit
 Note:A majority circuit is a combinational circuit whose output is equal to 1
if the input variables have more 1's than 0's. The output is 0 otherwise
 Design a combinational circuit with 3 inputs X,Y,Z and 3
output A,B,C. When the binary input is 0,1,2,3 , the binary
output is one greater than the input. When the binary input is
4,5,6,7 , the binary output is one less than the input.
 Design a 4 bit 2’s Complement combinational circuit
 Design a 4 bit combinational circuit incrementer. (5 bit
output) 21

22.  Design a BCD to 7 Segment decoder
 I/P – 4 Bit
 O/P – a,b,c,d,e,f,g
 Design a 3 bit Binary to gray code Converter.
 Design a 4 bit gray to Binary Code Converter.
 Design a BCD to 8 4 -2 -1 code converter
22

23. 23
Design procedure
Code-Conversion example, first, we can list the relation of the BCD
and Excess-3 codes in the truth table.

24. 24
Karnaugh map
2. For each symbol of the Excess-3 code, we use 1’s
to draw the map for simplifying Boolean function.

25. 25
Circuit implementation
z = D’;y = CD + C’D’ = CD + (C + D)’
x = B’C + B’D + BC’D’ = B’(C + D) + B(C + D)’
w = A + BC + BD = A + B(C + D)

26. 26
Binary Adder-Subtractor
 A combinational circuit that performs the addition of two bits
is called a half adder.
 The truth table for the half adder is listed below:
S = x’y + xy’
C = xy
S: Sum
C: Carry

27. 27
Implementation of Half-Adder

28. 28
Full-Adder
 One that performs the addition of three bits(two
significant bits and a previous carry) is a full adder.

29. 29
Simplified Expressions
S = x’y’z + x’yz’ + xy’z’ + xyz
C = xy + xz + yz
C

30. 30
Full adder implemented in
SOP

31. 31
Another implementation
 Full-adder can also implemented with two half
adders and one OR gate (Carry Look-Ahead
adder).
S = z ⊕ (x ⊕ y)
= z’(xy’ + x’y) + z(xy’ + x’y)’
= xy’z’ + x’yz’ + xyz + x’y’z
C = z(xy’ + x’y) + xy = xy’z + x’yz + xy

32. 32
Binary adder
 This is also called
Ripple Carry
Adder ,because of
the construction with
full adders are
connected in
cascade.

33. 33
Carry Propagation
 Fig.4-9 causes a unstable factor on carry bit, and produces
a longest propagation delay.
 The signal from Ci to the output carry Ci+1, propagates
through an AND and OR gates, so, for an n-bit RCA, there
are 2n gate levels for the carry to propagate from input to
output.

34. 34
Carry Propagation
 Because the propagation delay will affect the output signals
on different time, so the signals are given enough time to get
the precise and stable outputs.
 The most widely used technique employs the principle of
carry look-ahead to improve the speed of the algorithm.

35. 35
Boolean functions
Pi = Ai ⊕ Bi steady state value
Gi = AiBi steady state value
Output sum and carry
Si = Pi ⊕ Ci
Ci+1 = Gi + PiCi
Gi : carry generate Pi : carry propagate
C0 = input carry
C1 = G0 + P0C0
C2 = G1 + P1C1 = G1 + P1G0 + P1P0C0
C3 = G2 + P2C2 = G2 + P2G1 + P2P1G0 + P2P1P0C0
 C3 does not have to wait for C2 and C1 to propagate.

36. 36
Logic diagram of
carry look-ahead generator
 C3 is propagated at the same time as C2 and C1.