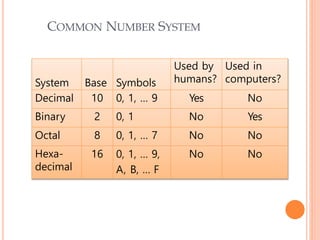
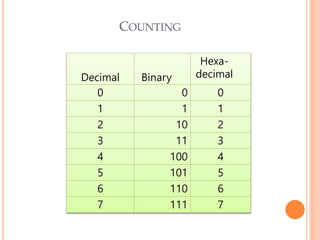
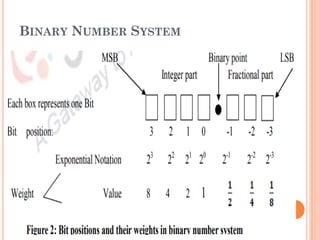
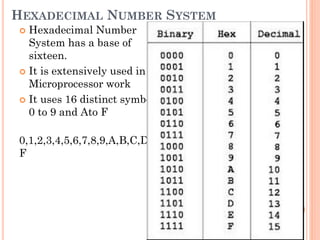
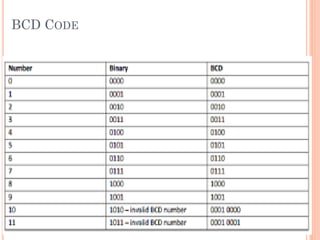
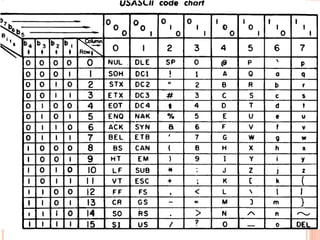
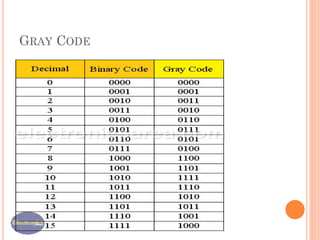
This document covers number systems including decimal, binary, hexadecimal and their representations. It discusses how to convert between different number bases including binary to decimal and hexadecimal to decimal. Binary operations like addition, subtraction and codes like binary coded decimal are explained. Non-weighted codes such as gray code are also introduced. Reference books on digital electronics and number systems are provided.

1. F.Y.B.SC.(C.SC.)
PRINCIPLES OF DIGITAL
ELECTRONICS- NUMBER SYSTEMS
-Prof. Vandana Pagar
Assistant professor
MIT ACSC.

2. TOPICS TO BE COVERED
➢Number Systems:
1. Decimal Number System
2. Binary Number System
3. Hexadecimal Number System
➢Representation of Numbers of
Different Radix
➢Conversion of Numbers from one Radix
to Another Radix

3. WHAT IS NUMBER SYSTEM ?
•system for representing number of certain type.
• Example:
–There are several systems for representing the
–counting numbers.
– These include the usual base “10” or decimal system : 1,2,3
,…..10,11,12,..99,100,…
,…..10,11,12,..99,100,…

4. System Base Symbols
Used by
humans?
Used in
computers?
Decimal 10 0, 1, … 9 Yes No
Binary 2 0, 1 No Yes
Octal 8 0, 1, … 7 No No
Hexa-
decimal
16 0, 1, … 9,
A, B, … F
No No
COMMON NUMBER SYSTEM

5. Decimal Binary
Hexa-
decimal
0 0 0
1 1 1
2 10 2
3 11 3
4 100 4
5 101 5
6 110 6
7 111 7
COUNTING

6. DECIMAL NUMBER SYSTEM
In Decimal number system, an
ordered set of ten symbols
0,1,2,3,4,5,6,7,8 and 9 are used to
specify the quantities.
Symbols used are known as digits.
Radix or base of decimal number
system is 10

7. DECIMAL NUMBER SYSTEM

8. BINARY NUMBER SYSTEM
 The binary number system is a code that uses
only two basic symbols i.e. 0 and 1
 Generally in digital electronics 0 represents low
level and 1 represents high level.
 Symbols in binary number system are called as
bits.

9. BINARY NUMBER SYSTEM

10. HEXADECIMAL NUMBER SYSTEM
 Hexadecimal Number
System has a base of
sixteen.
 It is extensively used in
Microprocessor work
 It uses 16 distinct symbols
0 to 9 and Ato F
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,
F

11. BINARY TO DECIMAL CONVERSION:
(i) Get the decimal number
(ii) Write the weights in exponential form
(iii) Place 1 and a 0 at appropriate positions i.e. place a
1 if weight is taken during the sum and 0 otherwise.
iv.) Add all the products

12. HEXADECIMAL TO DECIMAL
CONVERSION:
 In a hexadecimal number system each digit
position corresponds to power of 16. The weight
of the digit position in a hexadecimal number is
as follows:
▪ In hexadecimal number system each digit
position corresponds to appropriate power of 16.
The weights of the digit positions in hexadecimal
number are as follows:
………163 162 161 160 . 16-1 16-2 16-3
▪ To convert Hexadecimal number to decimal
number, multiply each hexadecimal digit by its
weight and add the resulting product.

13. DECIMAL TO ANY BASE
 Steps:
1. Convert integer part
( Successive Division Method )
2. Convert fractional part
( Successive Multiplication Method )

14. DECIMAL TO BINARY CONVERSION
Steps in Successive Division Method
1. Divide the integer part of decimal number by
desired base number, store quotient (Q) and
remainder (R)
2. Consider quotient as a new decimal number and
repeat step1 until quotient becomes 0
3. Note down the remainders in the reverse order

15. DECIMAL FRACTIONS TO BINARY
 Multiply Rule is used
 Multiply bit by two and record the carry in the
integer position
 Note down the integers in forward direction(top
to bottom).
(0.364) 10 = ( ?)2
0.364*2 = 0.728 0
0.728*2 = 1.456 1
0.456*2 = 0.912 0
0.912*2 =1.824 1
0.824*2= 1.648 1
Ans:(0.364) 10 = ( 0.01011)2

16. DECIMAL TO HEXADECIMAL

17. HEXADECIMAL TO BINARY
 To convert a hexadecimal number to a binary
number, first write each hexadecimal digit to its
4-bit equivalent using the binary codes, and then
write the binary numbers without a gap.
Example : Convert (9A)16 to binary equivalent.
Solution :- (9 A)
(1001 1010) 2
Thus (9A)16 = (1001 1010) 2

18. BINARY TO HEXADECIMAL CONVERSION
(BIN TO HEX) :
 Converting a binary to hexadecimal is a straight
forward procedure. Simply break the binary
number into four-bit groups starting at binary
point, and replace each group with the equivalent
hexadecimal symbol.
 Example : Convert (101101)2 to Hexadecimal
equivalent
10 1101
2 D
(101101)2=(2D)16

19. BINARY ADDITIONS
 Binary numbers are added like decimal
numbers.
 In decimal, when numbers sum more than 9 a
carry results.
 In binary when numbers sum more than 1 a
carry takes place.
0 + 0 = 0
1 + 0 = 1
1 + 1 = 0 + carry 1
1 + 1 + 1 = 1 + carry 1

20. BINARY CODED DECIMAL (BCD) CODE:-
 The binary coded decimal (BCD) code is a
weighted code. This code is found very convenient
for representing digits. Each group of four bits is
used to represent one decimal digit. It is also
called as 8421 code. This code consists of four bits
which have the weights as 8 4 2 1 . The four bit
combination that represents the decimal digits 0
to 9 are shown in table 1.4.

21. BCD CODE

22. BINARY SUBTRACTION:
 To perform a binary subtraction you first have to
represent the number to be subtracted in its negative
form. This is known as its two's complement.
 The two's complement of a binary number is obtained
by:
1. Replacing all the 1s with 0s and the 0s with 1s. This is
known as its one's complement.
2. Adding 1 to this number by the rules of binary
addition.
Now you have the two's complement.
Example:
The decimal subtraction 29 - 7 = 22 is the same as
adding (29) + (-7) = 22
1. Convert the number to be subtracted to its two's
complement:

23. 2’S COMPLEMENT SUBTRACTION
00000111 (decimal 7)
11111000 (one's complement)
+ 00000001 (add 1)
11111001 (two's complement)
29 00011101
+-7 11111001
22 (1)00010110

24. NON-WEIGHTED CODES:-
 Non-weighted binary codes do not follow the
positional weight principle. The example of non-
weighted codes is gray codes, excess-3 code and
alphanumeric code etc.
 Alphanumeric Code:- In communication
along with ordinary number, we need some
characters, punctuation marks and also
control signals. The code we have studied so
far is not enough for data communication. For
overcoming this problem binary symbols are
used for representing number, alphabetic
character and special symbols.
 The binary codes which are uses to represents
number, alphabetic character and special symbol
are called alphanumeric code.
 ASCII
 EBCDIC

25. ASCII Code
 The ASCII code is extensively used for data
communication and in computers. It is a 7-bit
code, so it can represents 27 or 128 different
characters.
 It can represent decimal number 0-9, letters of
alphabets in lower case and upper case, special
symbol and control instructions. Each symbol has
7- bit code which is made up of a 3-bit group
followed by a 4-bit group. The number is
represented by 8421 code.

27. GRAY CODE:
 Binary to Gray Converter: In this conversion
the most significant bit (MSB) is copied as it is,
so these represents MSB of gray code, then going
from left to right add each adjacent pair of binary
digits to get the next gray code. After the
addition forget the about carry.

28. GRAY CODE

29. GRAY TO BINARY CODE CONVERSION
 In this conversion first write MSB bit as it is of a
gray code, this one is an MSB bit of binary code,
and then add each MSB of binary code to the
next bit of gray code. If carry is generated then
neglect the carry.

30. REFERENCE BOOKS:
1. Digital Fundamentals: Floyd T.M., Jain R.P., Pearson
Education
2. Digital Electronics: Jain R.P., Tata McGraw Hill
3. Digital Principles and Applications: Malvino Leach, Tata
McGraw-Hill
4. M.Morris Mano, “ Digital Design “ 3rdEdition, PHI,
NewDelhi.