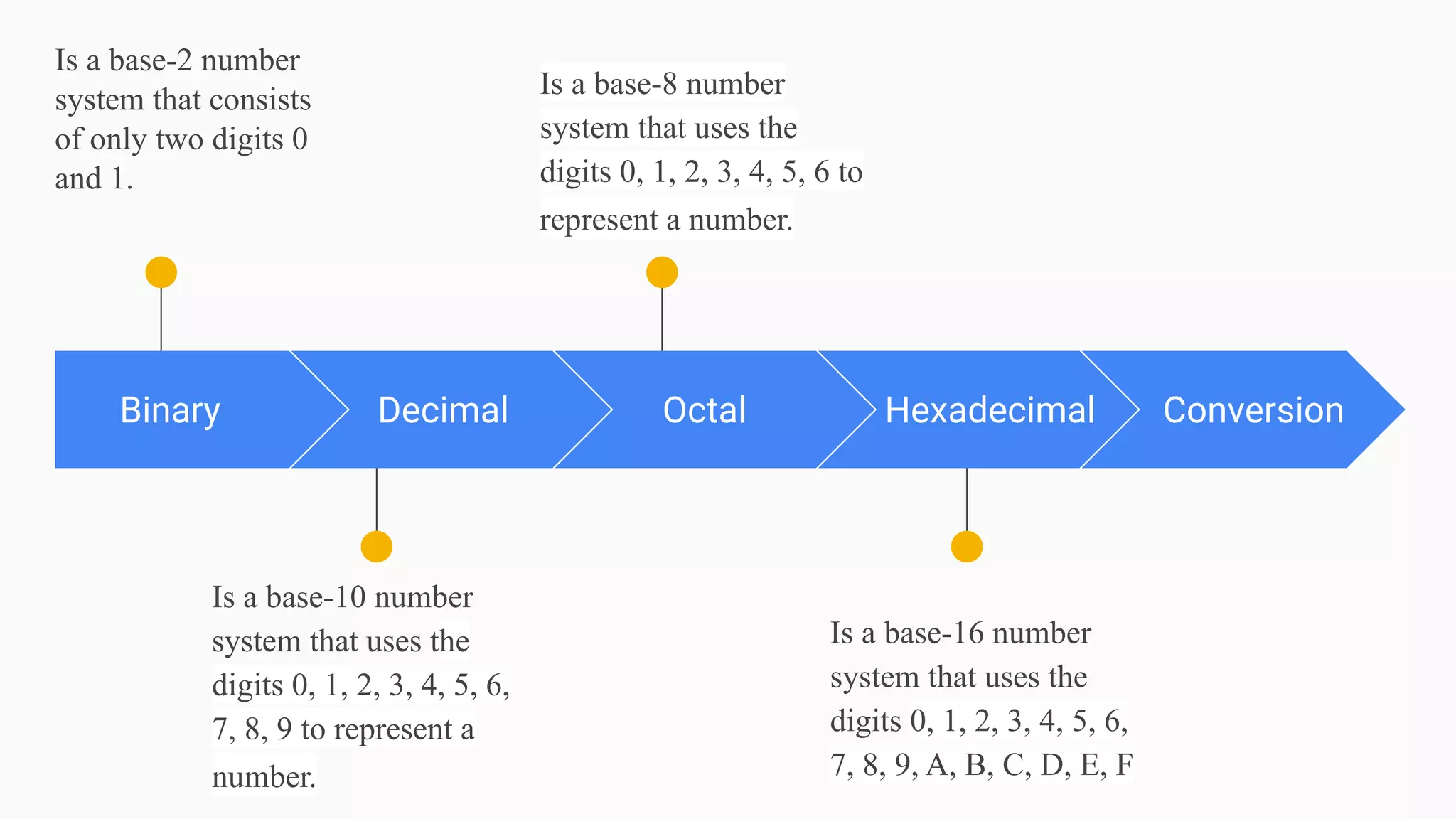
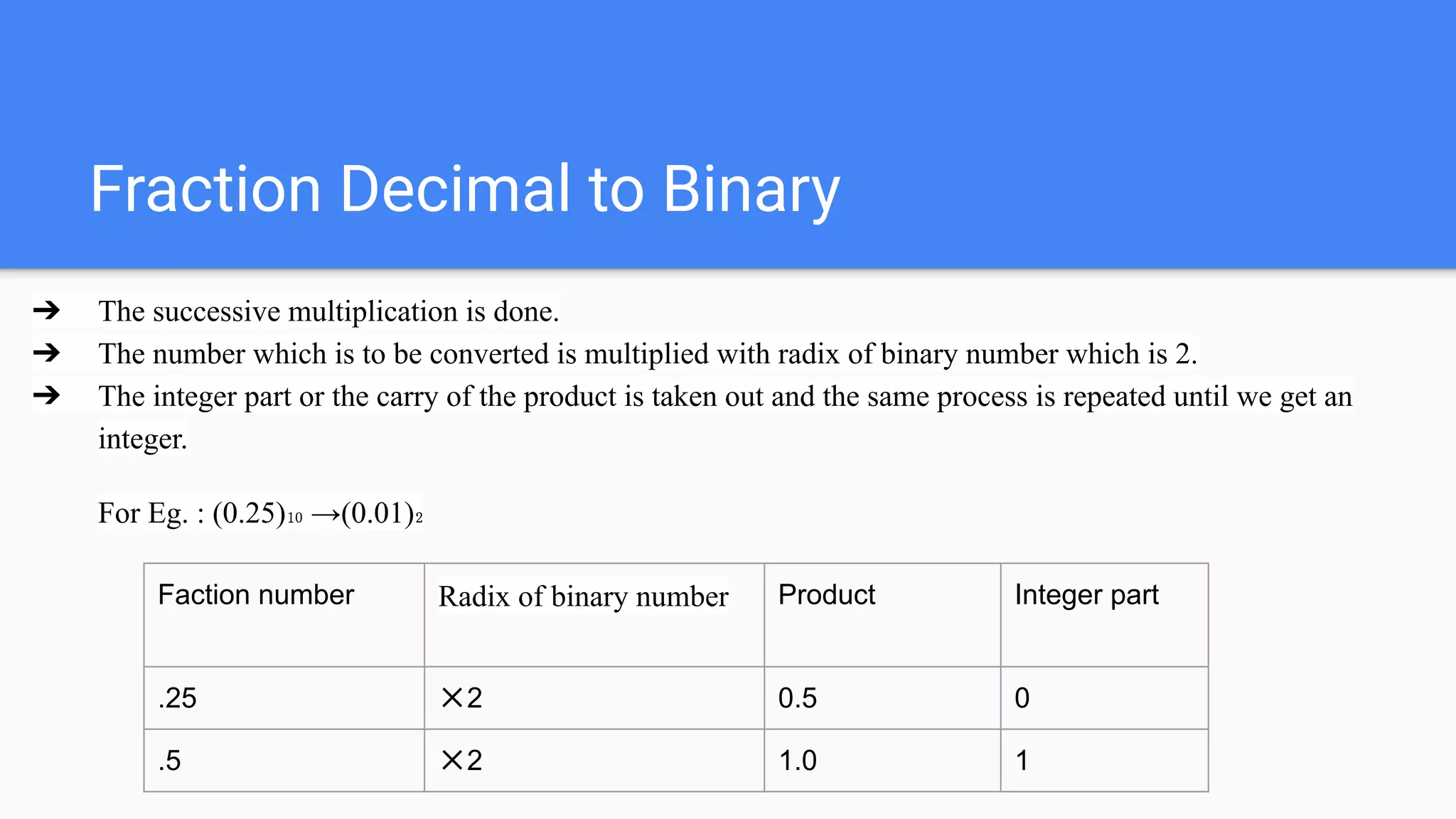
The document provides an introduction to digital electronics, focusing on digital signals and number systems such as binary, decimal, octal, and hexadecimal. It details conversion methods between these systems, binary arithmetic, and various coding techniques including error detection and correction. Additionally, it covers alphanumeric codes used to represent characters in digital form.

1. Digital Electronics

2. Introduction to the digital world
Digital electronics is a field of electronics involving the study of digital signals. Digital electronic circuits are usually made from
large assemblies of logic gates, often packaged in integrated circuits.
Digital electronics operate on bits which are used to form binary words. The bits can be represented as binary, decimal, octal or
hexadecimal, or other form.

3. Lesson 1: Number System
and Representation
May 27, 2020

4. Content
● Decimal, Binary,
● Octal, Hexadecimal,
● 1‘s and 2‘s complements,
● Codes – Binary, BCD,
Excess 3, Gray,
Alphanumeric codes

5. Binary
Is a base-2 number
system that consists
of only two digits 0
and 1.
Decimal
Is a base-10 number
system that uses the
digits 0, 1, 2, 3, 4, 5, 6,
7, 8, 9 to represent a
number.
Octal
Is a base-8 number
system that uses the
digits 0, 1, 2, 3, 4, 5, 6 to
represent a number.
Hexadecimal
Is a base-16 number
system that uses the
digits 0, 1, 2, 3, 4, 5, 6,
7, 8, 9, A, B, C, D, E, F
Conversion

6. Binary and Decimal Representation
Binary is a base-2 number system that uses two states 0 and 1 to represent a number, where
state 0 is also called as false state and state 1 is also called as true state.
Decimal is a base-10 number system that uses the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 to represent
a number.
For eg. : (1101)₂ → Base 2 written in radix represents a binary number.
(13)₁₀ → Base 10 written in radix represents a decimal number.
Note : If radix is not written in the base then by default it represents a decimal number.

7. Binary to Decimal Conversion
(1101)₂ → (13)₁₀
=1 ✕2³ + 1✕2² + 0✕2¹ + 1✕2⁰
=8+4+1 =(13)₁₀
Binary 1 1 0 1
Bit Position 2³ 2² 2¹ 2⁰
Bit Position
Label
MSB (most significant bit,
represents the left most bit)
LSB (least significant bit,
represents the right most
bit)

8. Binary to Decimal Conversion
(1110.011)₂ → (14.375)₁₀
=1 ✕2³ + 1✕2² + 1✕2¹ + 0✕2⁰ + 0✕ 2⁻¹ + 1✕2⁻² +1✕2⁻³
=8+4+2+0+0.25+0.125 =(14.375)₁₀
Binary 1 1 1 0 0 1 1
Bit
Position
2³ 2² 2¹ 2⁰ 2⁻¹ 2⁻² 2⁻³
Bit
Position
Label
MSB LSB
Note: This is the decimal
point
after the decimal point
the number should be
multiplied with 2⁻¹, 2⁻²,
2⁻³ and so on

9. Decimal to Binary Conversion
Divide the number by 2 and take only the remainder
(85)₁₀ → (1010101)₂
Divide 85 by 2 and get 42 as quotient and 1 as remainder,
Divide 42 by 2 and get 21 as quotient and 0 as remainder,
Divide 21 by 2 and get 10 as quotient and 1 as remainder,
Divide 10 by 2 and get 5 as quotient and 0 as remainder,
Divide 5 by 2 and get 2 as quotient and 1 as remainder,
Divide 2 by 1 and get 1 as quotient and 0 as remainder
remainder
2 85 1
2 42
(quotient)
0
2 21 1
2 10 0
2 5 1
2 2 0
1

10. Fraction Decimal to Binary
➔ The successive multiplication is done.
➔ The number which is to be converted is multiplied with radix of binary number which is 2.
➔ The integer part or the carry of the product is taken out and the same process is repeated until we get an
integer.
For Eg. : (0.25)₁₀ →(0.01)₂
Faction number Radix of binary number Product Integer part
.25 ✕2 0.5 0
.5 ✕2 1.0 1

11. Octal to Binary Conversion
Octal is a base-8 number system that uses the digits 0, 1, 2, 3, 4, 5, 6 to represent a
number.
For eg. : (367)₈ → (011 110 111)₂
For converting binary number to octal number
For eg. : (011010010101)₂ →(3225)₈
Note: Each significant digit in the given number is replaced by its 3-bit binary equivalent.
The conversion of octal to decimal can be done by multiplying each significant digit of the octal number by its
respective weight and adding the product.

12. Hexadecimal
Hexadecimal is a base-16 number system that uses the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B,
C, D, E, F to represent a number.
For eg. : (AB3)₁₆ → (2739)₁₀
=A×16² +B×16¹ +3×16⁰
=10×16² +11×16¹+3
=2560+176+3
=2739

13. Miscellaneous
Binary to decimal to octal to hexadecimal
(11010)₂→(26)₁₀→(32)₈→(1A)₁₆
=1×2⁴ +1×2³+0×2²+1×2¹+0×2⁰
=(26)₁₀
=(32)₈
=(011 010)₂ =(01 1010)₂
=(1A)₁₆
8 26 2
3

14. Arithmetic operation
Binary arithmetic
0+0=0
0+1=1
1+0=1
1+1=10
Binary subtraction
0-0=0
10-1=1
1-0=1
1-1=0
Binary multiplication
0×0=0
0×1=0
1×0=0
1×1=1
Binary division
0÷0=not allowed
0÷1=1
1÷0=not allowed
1÷1=1

15. 1’s complement and 2’s complement
1’s complement of a binary number is obtained by toggling all bits in it, i.e., transforming the
0 bit to 1 and the 1 bit to 0.
2’s complement of a binary number is 1 added to the 1’s complement of the binary number.
For eg. :
1’s complement of 0101 →1010
2’s complement of 0101 →1010+1→1011 (binary addition)

16. Codes
Codes is a symbolic representation of discrete information, which may be present in the form
of numbers, letters.
The symbols used are the binary digits 0 and 1.
Codes
Weighted binary
codes
Non-weighted
binary codes
Error detecting
codes
Error correcting
codes
Alphanumeric
codes

17. Weighted binary codes
It is a method of representing decimal
number by its binary equivalent.
The codes 8421, 2421, 5421 are weighted
binary codes.
Decimal
number
8421 5421 2421
0 0000 0000 0000
1 0001 0001 0001
2 0010 0010 0010
3 0011 0011 0011
4 0100 0100 0100
5 0101 1000 1011
6 0110 1001 1100
7 0111 1010 1101
8 1000 1011 1110
9 1001 1100 1111

18. Non -weighted binary codes
It is a code that each position within a binary number is not assigned a fixed value.
The codes excess-3 and gray codes are non -weighted binary codes.
Excess-3- It represents a decimal number in a binary form, as greater than 3. It is obtained by
adding 3 to decimal number.
For eg. :
Converting (634)₁₀ →to excess-3
The excess-3 code for
(634)₁₀ →100101100111
Decimal number: 6 3 4
Add 3 to each bit: +3 +3 +3
Sum: 9 6 7
BCD(8421 code) 1001 0110 0111

19. Non -weighted binary codes
Gray Codes is also known as minimum-change codes, in
which only one bit in the code group changes when moving
one step to the next.
For eg. : (1101)₂ to (1011)gray code
Step 1: First bit (MSB) is the same as the binary number
Step 2: Exclusive or of the first bit and second bit of binary
number.
Step 3: Exclusive or of the second bit and third bit of binary
number.
Step 4: Exclusive or of the third bit and fourth bit of binary
number.
1 1 0 1
1 0 1 1 (1101)₂ →(1011)
Decimal
number
Binary
code (8421)
Gray code
0 0000 0000
1 0001 0001
2 0010 0011
3 0011 0010
4 0100 0110
5 0101 0111
6 0110 0101

20. Non -weighted binary codes
Gray Codes is also known as minimum-change codes, in
which only one bit in the code group changes when moving
one step to the next.
For eg. : (1011) gray code to binay (1101)₂
Step 1: First bit (MSB) is the same as the gray number
Step 2: Exclusive or of the first bit of the binary and second
bit of gray number.
Step 3: Exclusive or of the second bit of binary number and
third bit of gray number
Step 4: Exclusive or of the third bit of binary number and
fourth bit of gray number.
1 0 1 1
1 1 0 1 (1011)→ (1101)₂
Decimal
number
(contd.)
Binary
code (8421)
Gray code
7 0111 0100
8 1000 1100
9 1001 1101
10 1010 1111
11 1011 1110
12 1100 1010
13 1101 1011
14 1110 1001
15 1111 1000

21. Error detecting codes and error correcting
codes
During binary data transmission, errors may occur. In order to detect and correct such errors,
two types of codes, error detecting and error correcting.
To detect and correct the errors, additional bits are added to the data bits at the time of
transmission.
● The additional bits are called parity bits. They allow detection or correction of the errors.
● The data bits along with the parity bits form a code word.

22. Parity checking of error detection
The MSB of an 8-bits word is used as the parity bit and the remaining 7 bits are used as data or
message bits. The parity of 8-bits transmitted word can be either even parity or odd parity.
P is the parity bit, d6-d0 is the data bits (7 bits)
Even parity -- Even parity means the number of 1's in the given word including the parity bit
should be even (2,4,6,....).
Odd parity -- Odd parity means the number of 1's in the given word including the parity bit
should be odd (1,3,5,....).
P
MSB
d6 d5 d4 d3 d2 d1 d0
LSB

23. Even parity and Odd parity
For even parity, parity bit is set to 1 or 0 such
that the no. of "1 bits" in the entire word is
even.
0
MSB
1 0 1 0 1 1 0
LSB
1
MSB
0 0 1 0 1 1 0
LSB
For odd parity, parity bit is set to 1 or 0
such that the no. of "1 bits" in the entire
word is odd.
0
MSB
1 0 1 0 0 1 0
LSB
1
MSB
0 0 1 0 0 1 0
LSB

24. Alphanumeric Codes
Alphanumeric codes are also called character codes, are binary codes used to represent
alphanumeric data.
The codes write alphanumeric data, including letters of the alphabet, mathematical symbols,
numbers, and punctuation marks, in a form that is understandable and process able by a
computer.
It includes; 26 lower case letters, 26 upper case letters, 10 numeric digits, 25 special characters.

25. Practise Problem
1) Convert decimal to binary number: (37)₁₀, (56)₁₀, (0.625)₁₀
2) Convert binary to decimal number : (11001)₂, (11.001)₂,
(1111)₂
3) Convert octal to binary number : (15)₈, (345)₈, (1254)₈
4) Convert hexadecimal to decimal : (49)₁₆, (AB0)₁₆, (649)₁₆
5) Convert binary to decimal to octal to hexadecimal: (110111)₂,
(1010)₂, (0011)₂
6) Express decimal numbers to excess-3 code : (426)₁₀, (520)₁₀,
(3421)₁₀
7) Convert binary to gray code: (1111)₂, (1110111)₂, (1000)₂
8) Convert gray to binary : (10111)g, (110011)g, (1000)g

26. THANKYOU