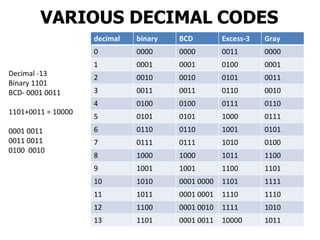
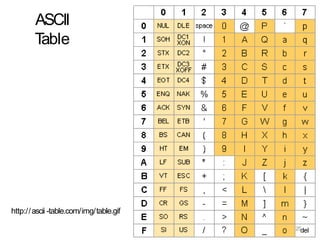
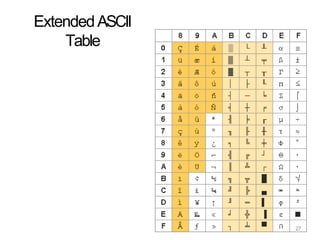
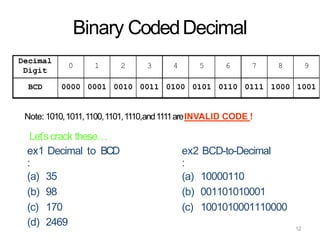
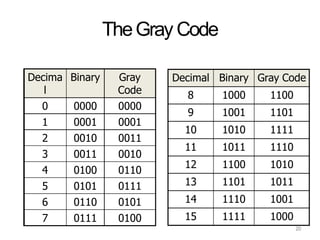
1. The document discusses different types of codes used to represent digital data including weighted, non-weighted, alphanumeric, error detection, error correction, and binary codes. 2. It describes various binary codes like BCD, Gray, EBCDIC, and ASCII codes explaining how they represent numeric and alphanumeric data. 3. Specific codes discussed in detail include BCD, excess-3, Gray, and ASCII codes explaining their binary representations of decimal numbers and characters.

1. Lecture on
Codes

2. Classification of Codes
The digital data is represented, stored and transmitted as group of bits. This group
of bits is also called as binary code.
1.Weighted& Non-weightedCode
2. Alphanumeric codes
3. Errordetection & ErrorcorrectionCodes
1. WeightedCodes
The main characteristic of weighted code is that each binary digit is assigned a specific
weight. The common example of weighted code is BCDcode or 8421 code in which the
weights of different bits are 1, 2, 4 & 8.
Eg; 1011 = 1x23 + 0x22 +1x21 + 1x20
Non-WeightedCode
Thesedon’t follow the principle of positional weighting system i.e. eachposition within the
number doesn’t follow or have any fixed weight. Foreg-Excess-3, Graycode.

3. • Cycliccodes:Cyclic codes are those in which each successive
code word differs from the preceding one in only one bit
position.
• Theyare also called unit distancecodes
• Example: graycode
MirrororReflectiveCode:
Example: Graycode.
00
01
10
11

4. AlphanumericCodes
• Apart from numericdata, a computersystemmayprocess
somealphanumericdata justlike the employees’names,
addressaswell assomespecialcharacters.AnAlphanumeric
data generallyconsistof sequenceof characterswhere a
characterisanyoneof the following:-
• Lettersor alphabets
• Digits0-9
• Specialcharacters(+,-,π)
• In the computersystem,eachcharacterisstored in some
codeform dependinguponthe codingscheme.The
charactermaytake 6, 7, or 8 bits. Thereare numberof codes
whichare usedfor somespecificapplicationi.e. ASCIICode,
EBCDICCode,UNITCode,etc.

5. Binarycodes:-BCD,GRAY,EBCDIC,ASCII
• It is the symbolic representation of discrete information which
may be represented in the form of numeric, alphabets &
special characters.
• In Digital Electronics, the binary digits 0 & 1 are used to
represent these symbols & are arranged according to the
rules of specific code.
• Infect, a binary code is a group of n-bits that can represent
distinct symbols.
• The interpretation of the binary information is possible only if
the code in which this information is available isknown.

6. Binarycodes:-BCD,GRAY,EBCDIC,ASCII
(A) Straight BinaryCode
Usedto represent numbers using natural (or straight) binary form.
1.Natural BCDCode
In this code, decimal 0 through 9 are represented by their natural binary
equivalents using four bits and each decimal digit is represented by this four bit
code individually. This code is also known as 8-4-2-1 code where 8, 4, 2, & 1 are
the weights of the four bits of the binary code of each decimal digit to the
straight binarysystem.
5 = 0101 , 8 = 1000, 9 =1001, 21 -0010 0001, 56 – 0101 0110
2.EXCESS-3Codes
This is another form of BCD code, in which each decimal is coded into a 4-bit binary code.
The code for each decimal digit is obtained by adding decimal 3 to the natural BCDcode of
the digit. For ex- decimal 2 is coded as0010+0011=0101 in Excess-3code.
0 = 0000 (BCD) + 0011 = 0011(Excess -3 code)
1=0001+0011= 0100 (excess – 3 code) , 8 = 1000+0011 =1011, 14 =0001 0100
0011 0011
01 0 0 01 1 1

7. Binarycodes:-BCD,GRAY,EBCDIC,ASCII
3. GrayCode
It is a very useful code in which a decimal number is represented in binary form in such a
way so that each gray code number differs from preceding & the succeeding number by a
single bit.
For ex- the gray code for decimal number 5 is 0111 & for 6 is 0101.
These two codes differ by only one bit position (third from left).
This code is used extensively for the shaft encoders because of this property.

8. VARIOUS DECIMAL CODES
decimal binary BCD Excess-3 Gray
0 0000 0000 0011 0000
1 0001 0001 0100 0001
2 0010 0010 0101 0011
3 0011 0011 0110 0010
4 0100 0100 0111 0110
5 0101 0101 1000 0111
6 0110 0110 1001 0101
7 0111 0111 1010 0100
8 1000 1000 1011 1100
9 1001 1001 1100 1101
10 1010 0001 0000 1101 1111
11 1011 0001 0001 1110 1110
12 1100 0001 0010 1111 1010
13 1101 0001 0011 10000 1011
Decimal -13
Binary 1101
BCD- 0001 0011
1101+0011 = 10000
0001 0011
0011 0011
0100 0010

9. Importance of Codes
1. Thecode refers to encryption system.
2.Computer and other digital circuits process datain
binary format.
3.Various binary codesare used to represent data.
4.Theinterpretation of data is only possible if the
code in which the information is available isknown.

10. 10
Binary CodedDecimal (BCD)
• Would it be easyfor you if you canreplacea
decimal number with an individual binary
code?
– Suchas0001 1001 = 1910
• The8421 code is atype of BCDto dothat.
• BCDcode provides an excellent interface to
binary systems:
– Keypadinputs
– Digital readouts

11. 11
Binary CodedDecimal (BCD)
– Usedto represent the decimal digits 0 -9.
– 4 bits areused.
– Eachbit position hasaweight associatedwith it ( weighted code).
– Weights are: 8, 4, 2, and 1 from MSBto LSB(called 8 -4-2-1code).
– BCDCodes:
0: 0000 4: 0100 8:1000
1: 0001 5: 0101 9:1001
2: 0010 6: 0110
3: 0011 7: 0111
– Usedto encode numbers for output to numericaldisplays
– Usedin processorsthat perform decimal arithmetic.
– Example:(9750)10=(1001 0111 0101 0000)BC
D
9 7 5 0

12. 12
Binary CodedDecimal
Decimal
Digit
0 1 2 3 4 5 6 7 8 9
BCD 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001
ex1
:
Decimal to BCD ex2
:
BCD-to-Decimal
(a) 35 (a) 10000110
(b) 98 (b) 001101010001
(c) 170 (c) 1001010001110000
(d) 2469
Note: 1010,1011,1100,1101,1110,and1111areINVALID CODE !
Let’scrack these…

13. 13
BCDAddition
• BCDis anumerical code and canbe used in
arithmetic operations. Here is how to add two BCD
numbers:
– Add the two BCDnumbers, using the rules forbasic binary
addition.
– If a4-bit sum is equal toor less than 9, it is avalid BCD
number.
– If a4-bit sum >9, or if acarry out of the 4 -bit group is
generated it is an invalid result.Add 6 (0110) to a4-bit sum
in order to skip the six invalid statesand return the code to
8421. If acarry results when 6 is added, simply add the
carry to the next 4-bit group.

14. 14
BCDAddition
• Trythese:
ex:Add the followingnumbers
(a) 0011+0100
(b) 00100011 + 00010101
(c) 10000110 + 00010011
(d) 010001010000 + 010000010111
(e) 1001 + 0100
(f) 1001 + 1001
(g) 00010110 + 00010101
(h) 01100111 + 01010011

15. 15
BCDSubtraction
• Here is how to subtract two BCDnumbers:
– Subtract the two BCDnumbers, using the rules forbasic
binary subtraction.
– If there is no borrow from the next higher group, no
correction isrequired.
– If there is borrow from the next group, then (0110) is
subtracted from the difference term of this group.
– Example38 – 15
38 0011 1000
15 0001 0101
(38 in BCD)
(15 in BCD)
–
– 0010 0011 (No borrow,
0010 1001 from 1011 0010
1101 0110 – 1’s of sub
1011 0010 - minuend +
11000 1000
1
1000 1001 st - 1
0000 1010
1000 0011 st-2

16. 16
BCDSubtraction
• Trythese:
ex:Add the followingnumbers
(a) 0011-0100
(b) 00100011 - 00010101
(c) 10000110 - 00010011
(d) 010001010000 - 010000010111
(e) 1001 - 0100
(f) 1001 - 1001
(g) 00010110 - 00010101
(h) 01100111 - 01010011

17. 17
TheGray Code
• TheGraycode is unweighted and is not an
arithmetic code.
– There are no specific weights assigned to thebit
positions.
• Important: the Graycode exhibits only asingle
bit change from one code word to the next in
sequence.
– Thisproperty is important in manyapplications,
suchasshaft position encoders.

18. TheGray Code
• Binary-to-Gray code conversion
– TheMSBin the Graycode is the sameas
corresponding MSBin the binary number.
– Going from left to right, add each adjacent pairof
binary code bits to get the next Graycode bit.
Discard carries.
ex: convert 101102 to Gray code
1 + 0 + 1 + 1 + 0 binary
1 1 1 0 1 Gray
18

19. TheGray Code
• Gray-to-Binary Conversion
– TheMSBin the binary code is the sameasthe
corresponding bit in theGraycode.
– Add each binary code bit generated tothe Graycode bit in
the next adjacent position. Discard carries.
ex:convert the Graycode word 11011 to binary
Gray Binary
1 1 0 1 1 - gray code
+ +
19
+ +
1 0 0 1 0

20. 20
TheGray Code
Decima
l
Binary Gray
Code
0 0000 0000
1 0001 0001
2 0010 0011
3 0011 0010
4 0100 0110
5 0101 0111
6 0110 0101
7 0111 0100
Decimal Binary Gray Code
8 1000 1100
9 1001 1101
10 1010 1111
11 1011 1110
12 1100 1010
13 1101 1011
14 1110 1001
15 1111 1000

21. Excess 3 Code
21
•A BCD Code formed by adding 3 (0011)
to its true four bit binary value.
•Excess 3 is a self complementing code. If
the bits of the Excess-3 digit are inverted,
they yield the 9’s complement of the
decimal equivalent.
•Excess-3 code is useful for performing
decimal arithmetic digitally.

22. Excess 3
22
Examples
• 3 = 0011 + 0011 = 0110 = 6 in E-3.
• 1 = 0001 + 0011 = 0100 = 4 in E-3
•If we complement 1’s = 1011 in E-3 this
is the code for an 8.
•9s Complement of 1(0100) = (9 - 1) = 8
Self Complement
• 6 = 0110+0011 = 1001
• 12 = 1100 + 0011 = 1111

23. 23
Alphanumeric Codes
• Representnumbers and alphabetic characters.
– Also represent other characters such as symbols
and various instructions necessary for conveying
information.
• The ASCIIis the most common alphanumeric
code.
– ASCII=American Standard Code for Information
Interchange

24. 24
ASCII
• ASCIIhas128 characters and symbols
represented by a7-bit binary code.
– It canbe considered an 8-bit code with theMSB
always 0. (00h-7Fh) (00h – 0Fh) =16
• 00h-1Fh (the first 32) – control characters
• 20h-7Fh – graphics symbols (can be printedor
displayed)

25. ASCII
T
able
http://ascii -table.com/img/table.gif
25

26. 26
Extended ASCII
• There are an additional 128 characters that
were adopted by IBM for usein their PCs.It’s
popular and is used in applications other than
PCs unofficial standard.
– TheextendedASCIIcharacters are represented by
an 8-bit code series from 80h-FFh

27. ExtendedASCII
Table
27