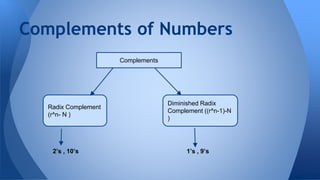
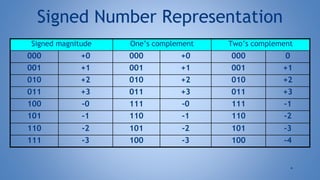
This document summarizes key concepts in digital systems and binary numbers. It discusses why digital systems are preferred over analog, how to convert between number bases, signed and complement number representations, overflow, binary and decimal codes, BCD addition, Gray code, and parity checks. Digital systems are more cost effective, reliable, programmable and selective compared to analog. Number conversions involve grouping bits or dividing decimals. Signed number systems use complement representations to indicate positive and negative values.

1. Chapter 1
Digital Systems and Binary Numbers

2. Key Concepts :
● Why digital Over Analog Systems ?
● Number - Base Conversions
● Complements of Numbers
● Signed Binary Number Systems
● OverFlow Concept
● Binary and Decimal Codes
● BCD Addition
● Gray Code
● Parity Check

3. Why Digital Over Analog ?
1. Reduced Cost
2. More Reliable
3. Programmable (so has major application)
4. Selective ( Akin to a Research Scientist vs
a Payroll Schedule)
5. Implemented via Electronic Components

4. Number Conversions
Convert From X ---- > Y Method
Any System(r) To Decimal Multiply Coefficients before Decimal by r ^
index. And Coefficients after Decimal by r^(-
index) where index starts from -1 after
decimal and 0 before.
Decimal to Any System (r) Divide Decimal by r Repeatedly and Collect
remainders. The Final Answer is From Last
Remainder Collected to First.
Binary To Octal Group in 3s
Binary To Hexadecimal Group in 4s

5. Convertion of 75.375 (decimal) to Binary
Therefore the answer is : (001011.011)

6. Complements of Numbers
Complements
Radix Complement
(r^n- N )
Diminished Radix
Complement ((r^n-1)-N
)
2’s , 10’s 1’s , 9’s

7. *
Signed Binary Numbers
We need to represent these symbols using bits
– Convention:
• 0 positive
1 negative
• The leftmost bit position is used as a sign bit
– In signed representation, bits to the right of sign bit is
the number
– In unsigned representation, the leftmost bit is a part of
the number (the most significant bit (MSB))

8. *
Example
– 01011 → (unsigned binary)
– → (signed binary)
– 11011 → (unsigned binary)
– → (signed binary)
– This method is called “signed-magnitude” and is rarely used in digital
systems (if at all)
• In computers, a negative number is represented by the complement of its
absolute value.
• Signed-complement system
– positive numbers have always “0” in the MSB position
– negative numbers have always “1” in the MSB position

9. *
Signed Number Representation
Signed magnitude One’s complement Two’s complement
000 +0 000 +0 000 0
001 +1 001 +1 001 +1
010 +2 010 +2 010 +2
011 +3 011 +3 011 +3
100 -0 111 -0 111 -1
101 -1 110 -1 110 -2
110 -2 101 -2 101 -3
111 -3 100 -3 100 -4

10. 8,4,2,1 and Excess Three Coding
● BCD : Involves each digit being
assigned appropriate binary code.
Eg : 123 = 0001-0010-0011
● In BCD Addition if sum is greater
than 10, then 0110 (6) added .
● 8,4,2,1 Coding is a Weighted
Code
● Excess 3 Code: Is Binary Code
+3 . Therefore it is NOT A
weighted Code.
● Excess 3 is a SELF
COMPLIMENTING CODE.

11. GRAY CODE
● Used when digital data to analog data
is converted
● Only one bit in group changes from
one number to another
● Used in cases where normal binary
sequence may produce error
● Non Weighted Code

12. Parity Check
Used Often in Transmission Of
Messages.
If message is received : ACK
returned.
Else ,
NAK returned.

13. By :
Debarati Das
1PI13CS052
PES University