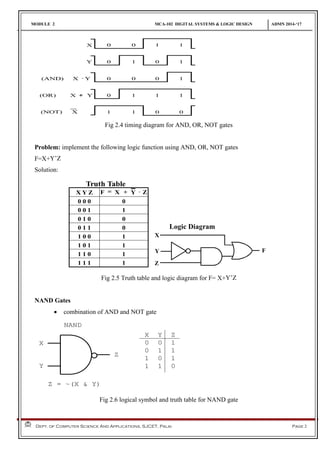
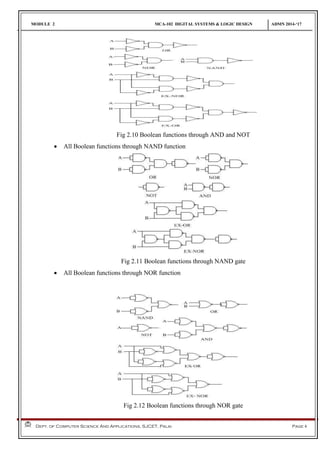
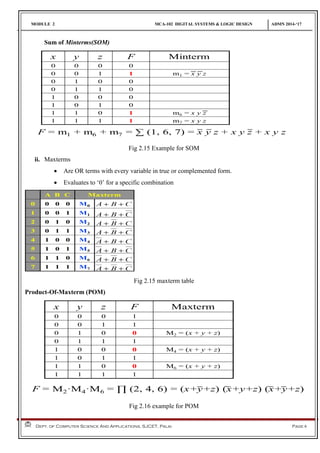
This document discusses logic gates and Boolean algebra. It begins by defining basic logic gates like AND, OR, and NOT. It then covers more advanced gates like NAND, NOR, XOR, and XNOR and provides their truth tables. The document explains how to implement logic functions using gates. It also covers Boolean algebra topics like Boolean functions, minterms, maxterms, SOP, POS, Karnaugh maps, and their use in minimizing logic expressions. Worked examples are provided for implementing functions with gates and simplifying expressions using K-maps.

1. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 1
Logic Gates
 Basic logical operators are the logic functions AND, OR and NOT.
 Logic gates implement logic functions.
 The three basic logical operations are:
1. AND
2. OR
3. NOT
1. AND Gates
 Is denoted by a dot (·).
Fig 2.1 truth table and logical symbol for AND gate
2. OR Gates
 Is denoted by a plus (+).
Fig 2.2 logical symbol and truth table for OR gate
3. NOT Gates
 is denoted by an over bar ( ¯ ),
Fig 2.3 logical symbol and truth table for NOT gate

2. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 2
Fig 2.4 timing diagram for AND, OR, NOT gates
Problem: implement the following logic function using AND, OR, NOT gates
F=X+Y’Z
Solution:
Fig 2.5 Truth table and logic diagram for F= X+Y’Z
NAND Gates
 combination of AND and NOT gate
Fig 2.6 logical symbol and truth table for NAND gate

3. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 3
NOR Gate
 combination of OR and NOT gate
Fig 2.7 logical symbol and truth table for NOR gate
XOR (Exclusive-OR) Gate
x
y
x Å y
x y + x y
Fig 2.8 logic symbol and truth table for XOR gate
XNOR (Exclusive-NOR Gate)
x
y
x Å y
x  y
x y + x y
Fig 2.9 logic symbol and truth table for XNOR gate
Boolean algebra
 a useful mathematical system for specifying and transforming logic functions
 Boolean Functions: is an expression formed with binary variables, the 2 two binary operators OR
and AND, and unary operator NOT, parentheses, and an equal sign.
 For a given value of the variables, the function can be either 0 or 1.
 A Boolean function has:
i. At least one Boolean variable,
ii. At least one Boolean operator, and
iii. At least one input from the set {0, 1}.
 It produces an output that is also a member of the set {0, 1}.
 All Boolean functions through AND and NOT operations

4. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 4
Fig 2.10 Boolean functions through AND and NOT
 All Boolean functions through NAND function
Fig 2.11 Boolean functions through NAND gate
 All Boolean functions through NOR function
Fig 2.12 Boolean functions through NOR gate

5. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 5
Fig 2.13 Boolean algebra Laws
 A Boolean expression can be represented in
i. Minterms
ii. Maxterms
iii. SOP (Sum Of Products)
iv. POS (Product of Sums)
i. Minterms
 Are AND terms with every variable present in either true or complemented form.
 Evaluates to ‘1’ for a specific combination
Fig 2.14 Minterm table

6. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 6
Sum of Minterms(SOM)
Fig 2.15 Example for SOM
ii. Maxterms
 Are OR terms with every variable in true or complemented form.
 Evaluates to ‘0’ for a specific combination
Fig 2.15 maxterm table
Product-Of-Maxterm (POM)
Fig 2.16 example for POM

7. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 7
iii. SOP (Sum of Products)
 equations are written as an OR of AND terms
 Implementation of this form is a two-level network of gates such that:
 The first level consists of n-input AND gates
 The second level is a single OR gate
 This form often can be simplified so that the corresponding circuit is simpler.
Iv.Product of Sum (POS)
 equations are written as an AND of OR terms
 ))()(( CBBACAF 
Minterms and maxterms are related

8. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 8
Converting Between Standard Forms
Example

9. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 9
Example 1.
Karnaugh-Map
• A Karnaugh map is a graphical method used to obtain the most simplified form of an expression in
a standard form (Sum-of-Products or Product-of-Sums).
• The simplest form of an expression is the one that has the minimum number of terms with the least
number of literals (variables) in each term.
• An n-variable K-map has 2n
cells with each cell corresponding to a row of an n-variable truth table.
• K-map cells are labeled with the corresponding truth-table row.
• K-map cells are arranged such that adjacent cells correspond to truth rows that differ in only one bit
position (logical adjacency).
• For the case of 2 variables, we form a map consisting of 22
=4 cells as shown in Figure

10. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 10
Fig 2.17 2 variable K-Map
 3 variables Karnaugh map
Fig 2.18 3 variable K-Map
 4 variables Karnaugh map
Fig 2.19 4 variable K-Map
 The Karnaugh map is completed by entering a '1‘(or ‘0’) in each of the appropriate cells.
 Within the map, adjacent cells containing 1's (or 0’s) are grouped together in twos, fours, or eights.
  CB(0,4)f   BA(4,5)f   B(0,1,4,5)f   A(0,1,2,3)f
BC
00
0
01
1
11 10A
1 0 0 0
1 0 0 0
BC
00
0
01
1
11 10A
0 0 0 0
1 1 0 0
BC
00
0
01
1
11 10A
1 1 1 1
0 0 0 0
BC
00
0
01
1
11 10A
1 1 0 0
1 1 0 0
  CA(0,4)f   CA(4,6)f   CA(0,2)f   C(0,2,4,6)f
BC
00
0
01
1
11 10A
0 1 1 0
0 0 0 0
BC
00
0
01
1
11 10A
0 0 0 0
1 0 0 1
BC
00
0
01
1
11 10A
1 0 0 1
1 0 0 1
BC
00
0
01
1
11 10A
1 0 0 1
0 0 0 0
Fig 2.20 examples of simplication of 3 variable k-map

11. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 11
  DCB(0,8)f   DCB(5,13)f   DBA(13,15)f   DBA(4,6)f
  CA(2,3,6,7)f   DB)(4,6,12,14f   CB)(2,3,10,11f   DB(0,2,8,10)f
CD
00
00
01
01
11
11
10
10
AB
1 0 0 0
0 0 0 0
0 0 0 0
1 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 0 0
0 1 0 0
0 1 0 0
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 0 0
0 0 0 0
0 1 1 0
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 0 0
1 0 0 1
0 0 0 0
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 1 1
0 0 1 1
0 0 0 0
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 0 0
1 0 0 1
1 0 0 1
0 0 0 0
CD
00
00
01
01
11
11
10
10
AB
0 0 1 1
0 0 0 0
0 0 0 0
0 0 1 1
CD
00
00
01
01
11
11
10
10
AB
1 0 0 1
0 0 0 0
0 0 0 0
1 0 0 1
Fig 2.21 examples for 4 variable K-Map
Example:
F(W,X,Y,Z)= ∏ M(0,2,3,4,5,6)
= Σm(1,7,8,9,10,11,12,13,14,15)
F(W,X,Y,Z)= W + XYZ + X’Y’Z

12. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 12
Don't Cares
 In certain cases some of the minterms may never occur or it may not matter what happens if they
do.In such cases we fill in the Karnaugh map with and X meaning don't care. When minimizing an
X is like a "joker" X can be 0 or 1 - whatever helps best with the minimization.
Ex:
Simplifies to B if x=1
Ex: simplify the expression using K-map for the truth table given below

13. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 13
Ex: Find a minimal SOP expression from the following 4 variable K-Map
M(A,B,C,D) = B D + A’ B’
Problem 1: Determine the minimum-cost SOP and POS expressions for the function f(x1, x2, x3, x4) =
_∑m(4, 6, 8, 10, 11, 12, 15) + D(3, 5, 7, 9).
Fig 2.22 Karnaugh maps for problem 1

14. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 14
Problem2: Use Karnaugh maps to find the minimum-cost SOP and POS expressions for the function
f(x1, . . . , x4) = x1x3x4 + x3x4 + x1x2x4 + x1x2x3x4
assuming that there are also don’ t-cares defined as D= ∑(9,12,14).
Fig 2.23 Karnaugh maps for problem 2
K-map with five variables
A 5-variable K-Map will have 25
= 32 cells. A function F which has maximum decimal value of 31,
can be defined and simplified by a 5-variable Karnaugh Map.
Fig 2.24 5 variable k-Map

15. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 15
Example 1
Given function, F = Σ (1, 3, 4, 5, 11, 12, 14, 16, 20, 21, 30)
Since, the biggest number is 30, we need to have 5 variables to define this function.
Fig 2.25 5 variable k-map for example 1
Applying rules of simplifying K-Map, there is no octet. There is one quad that is obtained by
visualizing Second Square on first, there are 4 adjacent cells – 4,5,20 and 21. The octet is highlighted by a
blue connecting line. There are 5 pairs. Similar to quad, there is one pair between two squares which is
highlighted by the blue connecting line.
(4, 5, 20, 21) – B’CD’ (Since A & E are the changing variables, it is eliminated)
(12, 14) – A’BCE’ (Since D is the changing variable, it is eliminated)
(14, 30) – BCDE’ (Since A is the changing variable, it is eliminated)
(3, 11) – A’C'DE (Since B is the changing variable, it is eliminated)
(16, 20) – AB’D'E’ (Since C is the changing variable, it is eliminated)
(1, 3) – A’B'C’E (Since D is the changing variable, it is eliminated)
Thus, F = B’CD’ + A’BCE’ + BCDE’ + A’C'DE + AB’D'E’ + A’B'C’E
Example 2
Given function, F = Σ (0, 2, 3, 5, 7, 8, 11, 13, 17, 19, 23, 24, 29, 30)
Since, the biggest number is 30, we need to have 5 variables to define this function.

16. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 16
Fig 2.26 solution for example 2
Applying rules of simplifying K-Map, there is no octet. First we need to look for quads within each
of the squares. There are none but there is a quad between two squares that is obtained by visualizing
Second Square on first, there are 4 adjacent cells – 3, 7, 19 and 23. This quad is highlighted by blue
connecting line. There are 6 pairs, out of which two are between two squares, highlighted by blue
connecting line.
(3, 7, 19, 23) - B’DE (Since A & C are the changing variables, they are eliminated)
(3, 11) – A’C'DE (Since B is the changing variables, it is eliminated)
(1, 2) – A’B'C’E’ (Since D is the changing variables, it is eliminated)
(5, 7) – A’B'CE (Since D is the changing variables, it is eliminated)
(17, 19) – AB’C'E (Since D is the changing variables, it is eliminated)
(13, 29) – BCD’E (Since A is the changing variables, it is eliminated)
(8, 24) – BC’D'E’ (Since A is the changing variables, it is eliminated)
There is 1 in cell 30, which cannot be looped with any adjacent cell, hence it cannot be simplified
further and left as it is.30 – ABCDE’
Thus, F = B’DE + A’C'DE + A’B'C’E’ + A’B'CE + AB’C'E + BCD’E + BC’D'E’ + ABCDE’

17. MODULE 2 MCA-102 DIGITAL SYSTEMS & LOGIC DESIGN ADMN 2014-‘17
Dept. of Computer Science And Applications, SJCET, Palai Page 17
Example 3
Given function, F = Σ (0, 1, 2, 3, 8, 9, 16, 17, 20, 21, 24, 25, 28, 29, 30, 31)
Since, the biggest number is 31, we need to have 5 variables to define this function.
Fig 2.27 solution for example 3
Applying rules of simplifying K-Map, there are 2 octets. First one is in square 2 circled in red.
Another octet is between 2 squares highlighted by blue connecting lines. There are 2 quads between each
of the squares.
(16, 17, 20, 21, 28, 29, 24, 25) – AD’ (Since B, C and E are changing variables, they are eliminated)
(0, 1, 8, 9, 16, 17, 24, 25) – C’D’ (Since A, B and E are changing variables, they are eliminated)
(0, 1, 2, 3) – A’B'C’ (Since D and E are changing variables, they are eliminated)
(28, 29, 30, 31) – ABC (Since D and E are changing variables, they are eliminated)
Thus, F = AD’ + C’D’ + A’B'C’ + ABC