This document provides an introduction to digital electronics and digital signals. It discusses the basics of analog and digital signals, with digital signals taking on discrete voltage levels compared to the continuous variation of analog signals. The advantages of digital techniques are explained, such as increased noise immunity and reliability. Common number systems are introduced, including binary, octal, hexadecimal and decimal, along with methods for converting between them. The key concepts of bytes, coding and voltage assignments in digital circuits are also covered at a high level.

1. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Introduction of Digital Techniques and Concepts:
All of us are familiar with the impact of Modern Digital Computers, Calculators, Watches, etc.one of the main causes
of this revolution is the advent of Integrated Circuits. (IC)
There are two basic types of Electronic Signals and techniques of analog and digital.
An analog signal is an AC or DC voltage or current that varies smoothly or continuously.
The fig shows the type of analog signal a sine wave. A significant number of electronic signals are sinusoidal. A
fixed DC voltage is also an analog signal.
Digital Signal;
Digital signals are essentially a series of pulses or rapidly changing voltage levels that vary in discrete steps. Digital
signals are pulses of voltage that switch between two fixed levels.
Electronic circuits that process these digital signals are called digital circuits.
Why Digital?
 Increased Noise Immunity
 Reliable
 Inexpensive
 Programmable
 Easy to Compute Nonlinear Functions
 Reproducible
 Small
 Most analog systems were less accurate, and were slow in computation and performance.
 Digital system have the ability to work faster than analog equivalents, and can operate on very high
frequencies too.

2. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
 It was much economical than analog methodologies as the performance was faster
Applications of Digital Techniques:
1) Communication: It is used as TDM (Time Division Multiplexing). It converts simple amplitude signal into digital
signal.
2) Industry: Using digital machine we can find the error of motor shaft or control system.
Computer: Digital computer, digital techniques are used as semiconductor memories, e.g.: RAM, ROM, PROM,
EAROM, CAM, etc.
INTRODUCTION TO NUMBER SYSTEM: - Many number systems are in use in digital technology. The most
common are the decimal, binary, octal, and hexadecimal systems.
The decimal system is clearly the most familiar to us because it is a tool that we use every day. Some of other
commonly used number systems are Binary, Octal and Hexadecimal number systems.
DECIMAL SYSTEM:
We are familiar with the number system in which an ordered set often symbols 0 through 9 known as digits. A
collection of these digits makes a number which in general has two parts integer and fractional.
are used to specify any number this system is popularly known as decimal system.
The radix or base of this number system is 10. Any number is collection of these digits.
103 102 101 100 10-1 10-2 10-3
=1000 =100 =10 =1 . =0.1 =0.01 =0.001
Most Significant Digit Decimal point
Least
Significant
Digit
BINARY NUMBER SYSTEM:-
The number system with base (radix) 2 is known as the binary number system. Only two symbols are used to
represent numbers in this system and these are 0 & 1. These are known as bits.
23 22 21 20 2-1 2-2 2-3
=8 =4 =2 =1 . =0.5 =0.25 =0.125
Most Significant Digit Binary point
Least
Significant
Digit
.

3. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
VOLTAGE ASSIGNMENT:
Binary 1: Any voltage between 2V to 5V
Binary 0: Any voltage between 0V to 0.8V
Not used: Voltage between 0.8V to 2V in 5 Volt CMOS and TTL Logic, this may cause error in a digital circuit.
Today's digital circuit’s works at 1.8 volts, so this statement may not hold true for all logic circuits.
0-low, off, false, open
1-high, on, true, close
BYTE & NIBBLE: Digital systems work in a binary fashion in which only two digits 0 and 1 known as bits. Are used
to specify any number a group of eight bits is known as byte and a group of four bits is known as a nibble.
CODING: Since a digital system understand 0’s and 1’s. Any information, which is usually in numerals, alphabetic
or alphanumeric form is to be suitably converted into the binary language before it can be processed by digital
circuits. This process is known as coding.
OCTAL NUMBER SYSTEM:-
This system is used in many computers and microcomputers for entering data. The number system with base 8 is
known as the octal number system. In this eight symbols 0, 1, 2, 3, 4, 5, 6&7 are used to represent numbers.
83 82 81 80 8-1 8-2 8-3
=512 =64 =8 =1 . =1/8 =1/64 =1/512
Most Significant Digit Octal point
Least
Significant
Digit
HEXADECIMAL NUMBERS:-
The hexadecimal system uses base 16. Thus, it has 16 possible digit symbols. It uses the digits 0 through 9 plus
the letters A, B, C, D, E, and F as the 16 digit symbols

4. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
163 162 161 160 16-1 16-2 16-3
=4096 =256 =16 =1 . =1/16 =1/256 =1/4096
Most Significant Digit Hexa Decimal point
Least
Significant
Digit
CODE CONVERSION
BINARY-TO-DECIMAL CONVERSION
Any binary number can be converted to its decimal equivalent simply by summing together the weights of the
various positions in the binary number which contain a 1.
Binary Decimal
110112
24+23+01+21+20 =16+8+0+2+1
Result 2710
Binary Decimal
101101012
27+06+25+24+03+22+01+20 =128+0+32+16+0+4+0+1
Result 18110
We should have noticed that the method is to find the weights (i.e., powers of 2) for each bit position that contains a
1, and then to add them up.
DECIMAL-TO-BINARY CONVERSION
Repeat Division-Convert decimal to binary
This method uses repeated division by 2.
Convert 2510 to binary
Division Remainder Binary
25/2 = 12+ remainder of 1 1 (Least Significant Bit)
12/2 = 6 + remainder of 0 0
6/2 = 3 + remainder of 0 0
3/2 = 1 + remainder of 1 1

5. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
1/2 = 0 + remainder of 1 1 (Most Significant Bit)
Result 2510 = 110012
BINARY-TO-OCTAL / OCTAL-TO-BINARY CONVERSION
Binary Equivalent Octal Digit
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7
Each Octal digit is represented by three binary digits.
Example:100 111 0102 = (100) (111) (010)2 = 4 7 28
DECIMAL TO OCTAL
This method uses repeated division by 8.
Example: Convert 17710 to octal and binary
Division Result Binary
177/8 = 22+ remainder of 1 1 (Least Significant Bit)
22/ 8 = 2 + remainder of 6 6
2 / 8 = 0 + remainder of 2 2 (Most Significant Bit)
Result 17710 = 2618
Binary = 0101100012

6. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
HEXADECIMAL TO DECIMAL CONVERSION
Example: 2AF16 = 2 x (162) + 10 x (161) + 15 x (160) = 68710
Decimal to Hexadecimal
This method uses repeated division by 16.
Example: convert 37810 to hexadecimal and binary:
Division Result Hexadecimal
378/16 = 23+ remainder of 10 A (Least Significant Bit)23
23/16 = 1 + remainder of 7 7
1/16 = 0 + remainder of 1 1 (Most Significant Bit)
Result 37810 = 17A16
Binary = 0001 0111 10102
BINARY-TO-HEXADECIMAL /HEXADECIMAL-TO-BINARY CONVERSION
Binary Equivalent 0000 0001 0010 0011 0100 0101 0110 0111
Hexadecimal Digit 0 1 2 3 4 5 6 7
Each Hexadecimal digit is represented by four bits of binary digit.
OCTAL-TO-HEXADECIMAL HEXADECIMAL-TO-OCTAL CONVERSION
Convert Octal (Hexadecimal) to Binary first.
Regroup the binary number by three bits per group starting from LSB if Octal is required.
Regroup the binary number by four bits per group starting from LSB if Hexadecimal is required.
Convert 5A816 to Octal.
Hexadecimal Binary/Octal
5A816 = 0101 1010 1000 (Binary)
= 010 110 101 000 (Binary)
Result = 2 6 5 0 (Octal)
1000 1001 1010 1011 1100 1101 1110 1111
8 9 A B C D E F

7. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
HEXADECIMAL TO DECIMAL CONVERSION
24.616 = 2 x (161) + 4 x (160) + 6 x (16-1) = 36.37510
11.116 = 1 x (161) + 1 x (160) + 1 x (16-1) = 17.062510
12.316 = 1 x (161) + 2 x (160) + 3 x (16-1) = 18.187510
OCTAL TO DECIMAL CONVERSION
2378 = 2 x (82) + 3 x (81) + 7 x (80) = 15910
24.68 = 2 x (81) + 4 x (80) + 6 x (8-1) = 20.7510
11.18 = 1 x (81) + 1 x (80) + 1 x (8-1) = 9.12510
12.38 = 1 x (81) + 2 x (80) + 3 x (8-1) = 10.37510
Some more examples:
- A binarynumbercan be convertedtodecimal byformingthe sumof powersof 2 of those coefficientswhose
value is 1.
(1010.011) 2 = 23
+ 21
+ 2-2
+ 2-3
= (10.375) 10
- Similarly,anumberexpressedinbase rcan be convertedtoitsdecimal equivalent bymultiplyingeach
coefficientwiththe correspondingpowerof rand adding.
(630.4) 8 = 6 x 82
+ 3 x 81
+ 0 x 80
+ 4 x 8-1
= (408.5) 10
- ConversionfromDecimal 41to Binary:
Integerquotient
Remainder Coefficient
41/2 = 20 + ½ a0 = 1
20/2 = 10 + 0 a1 = 0
10/2 = 5 + 0 a2 = 0
5/2 = 2 + ½ a3 = 1

8. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
2/2 = 1 + 0 a4 = 0
1/2 = 0 + ½ a5 = 1
- The conversionfromdecimal integerstoanybase-rsystemissimilartothe example,exceptthatdivisionis
done by r insteadof 2.
- Conversion fromDecimal 153 toOctal:
153
19 1
2 3
0 2 = (231) 8
- ConversionfromDecimal fraction(0.6875) 10 to Binary:
Integer
Fraction Coefficient
0.6875 x 2 = 1 + 0.3750 a-1 = 1
0.3750 x 2 = 0 + 0.7500 a-2 = 0
0.7500 x 2 = 1 + 0.5000 a-3 = 1
0.5000 x 2 = 1 + 0.0000 a-4 = 1
- The conversionfromdecimal fractiontoanybase-rsystemissimilartothe example.Multiplicationisby r
insteadof 2, and the coefficientsfoundfromthe integersmayrange invalue from0 to r-1 insteadof 0 and1.
- ConversionfromDecimal fraction(0.513) 10 to Octal:
0.513 x 8 = 4.104
0.104 x 8 = 0.832

9. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
0.832 x 8 = 6.656
0.656 x 8 = 5.248
0.248 x 8 = 1.984
0.984 x 8 = 7.872
(0.513) 10 = (0.406517…) 8
- The conversionof decimal numberswithbothintegersandfractionpartsisdone byconvertingthe integer
and fractionseparatelyandthencombiningthe twoanswers.
- Octal and Hexadecimal Numbers
- The conversionfromandto binary,octal and hexadecimalplaysanimportantpartindigital computers.Since
23
= 8 and 24
= 16, eachoctal digitcorrespondstothree binarydigitsandeachhexadecimal digitcorresponds
to fourbinarydigits.
- ConversionfrombinarytoOctal:
(10 110 001 101 011. 111 100 000 110) 2 = (26153.7406) 8
- ConversionfrombinarytoHexadecimal:
(10 1100 0110 1011. 1111 0000 0110) 2 = (2C6B.F06) 16
- ConversionfromOctal tobinary:
(673.124) 8 = (110 111 011. 001 010 100) 2
- Conversionfrom Hexadecimaltobinary:

10. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
(306.D) 16 = (0011 0000 0110. 1101) 2
- ConversionfromHexadecimaltoDecimal:
(37B) 16
3 x 162
+ 7 x 161
+ 11 x 160
= 3 x 256 + 7 x 16 + 11 x 1
= 768 + 112 +11
= (891) 10
8421 CODE/BCD CODE
Short for Binary Coded Decimal, BCD is also known as packet decimal and is numbers 0 through 9 converted to
four-digit binary. Below is a list of the decimal numbers 0 through 9 and the binary conversion.. The weights in the
BCD code are 8,4,2,1.
Decimal BCD
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001

11. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Using this conversion, the number 25, for example, would have a BCD number of 0010 0101 or 00100101.
However, in binary, 25 is represented as 11001.
Example: The bit assignment 1001, can be seen by its weights to represent the decimal 9 because:
1x8+0x4+0x2+1x1 = 9
Invalid BCD Numbers
These binary numbers are not allowed in the BCD code: 1010, 1011, 1100, 1101, 1110, and 1111
24 + 13 = 37
0010 0100 = 24
0001 0011 = 13
0011 0111 = 37
15 + 9 = 24
0001 0101 = 15
0000 1001 = 9
0001 1110 = 1? (invalid)
19 + 28 = 47
0001 1001 = 19
0010 1000 = 28
0100 0001 = 41 (error)
GRAY CODE
The gray code belongs to a class of codes called minimum change codes, in which only one bit in the code changes
when moving from one code to the next. The Gray code is non-weighted code, as the position of bit does not
contain any weight. The gray code is a reflective digital code which has the special property that any two
subsequent numbers codes differ by only one bit. This is also called a unit-distance code. In digital Gray code has
got a special place.
(1) The M.S.B. of the gray code will be exactly equal to the first bit of the given binary number.

12. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
(2) Now the second bit of the code will be exclusive-or of the first and second bit of the given binary number, i.e.
if both the bits are same the result will be 0 and if they are different the result will be 1.
(3)The third bit of gray code will be equal to the exclusive-or of the second and third bit of the given binary
number. Thus the Binary to gray code conversion goes on.
Decimal Number Binary Code Gray Code
0 0000 0000
1 0001 0001
2 0010 0011
3 0011 0010
4 0100 0110
5 0101 0111
6 0110 0101
7 0111 0100
8 1000 1100
9 1001 1101

13. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
GRAY TO BINARY CONVERSION
Gray Code MSB is binary code MSB.
Gray Code MSB-1 is the XOR of binary code MSB and MSB-1.
MSB-2 bit of gray code is XOR of MSB-1 and MSB-2 bit of binary code.
MSB-N bit of gray code is XOR of MSB-N-1 and MSB-N bit of binary code.
ASCII
ASCII (American Standard Code for Information Interchange) is the most widely used coding system to represent
data. The ASCII code is pronounced as ASKEE
ASCII is used on many personal computers and minicomputers.
ASCII is a 7-bit code that permits 27=128 distinct characters.
The 128 different combinations that can be represented in 7 bits are plenty to allow for all the letters, numbers and
special symbols.
Also, in ASCII, uppercase characters, lowercase characters and digits etc, are grouped together. So it is easy to
map between upper and lower case characters.
The ASCII table is divided in 3 different sections.
Non printable, system codes between 0 and 31.
Lower ASCII, between 32 and 127. This table originates from the older, American systems, which worked on 7-bit
character tables.
Higher ASCII, between 128 and 255. This portion is programmable; characters are based on the language of your
operating system or program you are using. Foreign letters are also placed in this section.

14. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
POSITIVE LOGIC
In a positive logic system, a high voltage is used to represent logical true (1), and a low voltage for a logical false
(0).
NEGATIVE LOGIC
In a negative logic system, a low voltage is used to represent logical true (1), and a high voltage for a logical
false (0).
In positive logic circuits it is normal to use +5V for true and 0V for false.
1’S AND 2’S COMPLEMENTS:
Introduction
 Subtraction of a number from another can be accomplished by adding the complement of the
subtrahend to the minuend.
1’s Complement Subtraction
 Subtraction of binary numbers using the 1’s complement method allows subtraction only by
addition.
 The 1’s complement of a binary number can be obtained by changing all 1s to 0s and all 0s and 1s.

15. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
 To subtract a smaller number from a larger number, the 1’s complement method is as follows
 Remove the carry and add it to the result. This carry is called end-around-carry
Example of 1’s complement
Subtraction Steps:
 Subtraction of a large number a smaller one by the 1’s complement method involves the following
steps
 The answer is the 1’s complement of the result and is opposite in sign. There is no carry.

16. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
2’s Complement Subtraction :
 The 2’s complement of a binary number can be obtained by adding 1 to its 1’s complement.
 Subtraction of a smaller number from a larger one by the 2’s complement method involves the
following steps
 Omit the carry ( there is always a carry in this case )
Example of 2’s complement:
Subtract (1010)2 from (1111) 2

17. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Subtraction Steps
 The carry is discarded. Thus answer is (0101)2
 The 2’s complement method for subtraction of a large number from a smaller one is as follows.
 To get an answer in true form, take the 2’s complement and change the sign.
Comparison between 1’s and 2’s complements
1’s Complement 2’s Complement
It can be easily obtained using
an Inverter
It has to be arrived at by first obtaining the
1’s complement and then adding one (1) to it
It requires two operations Only one arithmetic operation is required
It is often used in logical
manipulations for inversion
operation
It is used only for arithmetic
applications
Truth Tables
 Used to describe the functional behavior of a Boolean expression and/or Logic circuit.
 Each row in the truth table represents a unique combination of the input variables.
 For n input variables, there are 2n rows.
 The output of the logic function is defined for each row.
 Each row is assigned a numerical value, with the rows listed in ascending order.

18. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
 The order of the input variablesdefined in the logic function is important.
Boolean Expressions
 Boolean expressions are composed of
 Literals – variables and their complements
 Logical operations
 Examples
 F = A.B'.C + A'.B.C' + A.B.C + A'.B'.C'
 F = (A+B+C').(A'+B'+C).(A+B+C)
 F = A.B'.C' + A.(B.C' + B'.C)
 Boolean expressions are realized using a network (or combination) of logic gates.
 Each logic gate implementsone of the logic operations in the Boolean expression
 Each input to a logic gate represents one of the literalsin the Boolean expression
 Boolean expressions are evaluated by
 Substituting a 0 or 1 for each literal
 Calculating the logical value of the expression
 A Truth Table specifies the value of the Boolean expression for every combination of the variables
in the Boolean expression.
 For an n-variable Boolean expression, the truth table has 2n rows (one for each combination).
Boolean algebra:
George Boole developed an algebraic description for processes involving logical thought and
reasoning.
 Became known as Boolean Algebra
 Claude Shannon later demonstrated that Boolean Algebra could be used to describe switching
circuits.
 Switching circuits are circuits built from devices that switch between two states (e.g. 0 and
1).
 Switching Algebra is a special case of Boolean Algebra in which all variables take on just
two distinct values

19. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
 Boolean Algebra is a powerful tool for analyzing and designing logic circuits.
Basic Laws and Theorems

20. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Idempotence:
Complement:

21. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Distributive Law:

22. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Absorption (Covering)
Simplification:

23. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Logic Adjacency (Combining):

24. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag

25. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag

26. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag

27. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Proving DeMorgan's Law:

28. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
NAND equals “Negative OR”
NOR equals “Negative AND”

29. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Importance of Boolean Algebra
 Boolean Algebra is used to simplify Boolean expressions.
– Through application of the Laws and Theorems discussed
 Simpler expressions lead to simpler circuit realization, which, generally, reduces
cost, area requirements, and power consumption.
The objective of the digital circuit designer is to design and realize optimal digital circuits
Algebraic Simplification
 Justification for simplifying Boolean expressions:
– Reduces the cost associated with realizing the expression using logic gates.
– Reduces the area (i.e. silicon) required to fabricate the switching function.
– Reduces the power consumption of the circuit.

30. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
What are Logic Gates?
 Logic gates are the basic blocks of the digital circuits.
 There are basic gates of three types viz. AND, OR & NOT.
 Two universal gates are made of these 3 basic gates, which are NAND gate & NOR
gate.
 These gates are the basic functional blocks of digital circuits which work upon making
combinations of 0’s and 1’s !
 These are the sub-components of the IC’s !
What are Integrated Circuits (IC’s)?
 IC’s are the micro circuits which are fabricated on a very small silicon wafers (chip) at
which various components like BJT, CMOS etc. are mounted up to make a
wholesome functional unit.
 These days, various types of circuit integrations are possible at large extent, i.e. small
scale, large scale, and very large scale integration (VLSI).
(Analog Vs Digital) Electronics !!

31. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
SIMPLIFICATION OF BOOLEAN FUNCTIONS
The Map Method
- The Karnaugh mapmethodprovidesasimple,straightforwardprocedure forminimizingBooleanexpressions.
- The K-mapminimizationprocedure obtainsaminimal expressiondirectlyfromatruthtable.The map isa
diagrammade up of squarescontaining1sand/or0s.
- The map presentsavisual diagramof all possible waysafunctionmaybe expressedinastandardform.
- By recognizingvariouspatterns,the usercanderive alternative algebraicexpressionforthe same function.
Two- And Three- Variable Maps
MinimizationProcedure
1. Constructa K-map.
2. Findall groupsof horizontal orvertical adjacentsquaresthatcontain1.
a. Each group mustbe eitherrectangularorsquare with2n
squares.
b. Each group shouldbe as large as possible.
c. Each 1 on the K-mapmustbe coveredatleastonce.The same 1 can be includedinseveral groupsif
necessary.
d. Nonessential groupsare omitted.(A nonessential groupdoesnotcontaina1 that is not coveredby
any othergroup)
e. Adjacencyappliestobothvertical andhorizontal borders.

32. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
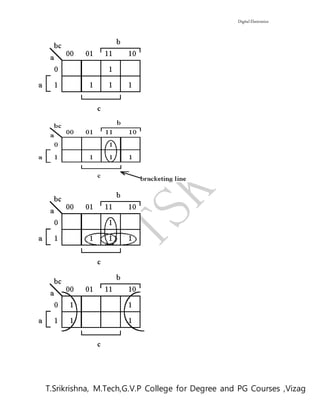
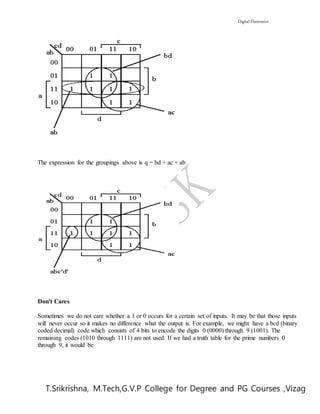
3. Translate eachgroup intoa product termby eliminatinganyvariable whose value changesfromcell tocell.
4. Sumall the productterms.
Note: Don't care conditionscanbe usedto provide furthersimplificationof the representationof afunction.
Given the following truth table for the function m:
The Boolean algebraic expression is
m = a'bc + ab'c + abc' + abc.
We have seen that the minimization is done as follows.
m = a'bc + abc + ab'c + abc + abc' + abc
= (a' + a)bc + a(b' + b)c + ab(c' + c) ]:[ aaNB 
= bc + ac + ab
The abc term was replicated and combined with the other terms.
To use a Karnaugh map we draw the following map which has a position (square) corresponding to each
of the 8 possible combinations of the 3 Boolean variables. The upper left position corresponds to the 000
row of the truth table, the lower right position corresponds to 110. Each square has two coordinates, the
vertical coordinate corresponds to the value of variable a and the horizontal corresponds to the values of b
and c.

33. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag

34. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
The expression for the groupings above is q = bd + ac + ab
Don't Cares
Sometimes we do not care whether a 1 or 0 occurs for a certain set of inputs. It may be that those inputs
will never occur so it makes no difference what the output is. For example, we might have a bcd (binary
coded decimal) code which consists of 4 bits to encode the digits 0 (0000) through 9 (1001). The
remaining codes (1010 through 1111) are not used. If we had a truth table for the prime numbers 0
through 9, it would be

35. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
The d’s in the above stand for "don't care", we don't care whether a 1 or 0 is the value for that combination
of inputs because (in this case) the inputs will never occur.
The minimized expression is
p = a'd + b'c
1. Construct Truth tables for each of the maps.

36. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
m =________________________ m= _______________________ m= _______________
1) Simplify the following function: F(a,b,c) = ∑mi (1,2,7,11,15) + ∑di (0,3,5,8)
Combinational vs. Sequential Circuits
Combinational circuits.
The output depends only on the current values of the inputs and not on the past values. Examples are
adders, subtractors, and all the circuits that we have studied so far
Sequential circuits.
The output depends not only on the current values of the inputs, but also on their past values. These hold
the secret of how to memorize information. We will study sequential circuits later.

37. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag

38. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag

39. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Half-Adder:
A combinational circuit which adds two one-bit binary numbers is called a half-adder. A
circuit which can perform the half add function.
If the carry from low bit is not considered, it is called half add.
However, we can perform both addition and subtraction using only adders because the
problem of subtraction becomes that of an addition when we use 1’s and 2’s complement representation of
negative numbers.
o The sum column resembles like an output of the XOR gate.

40. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
o The carry column resembles like an output of the AND gate.
Limitations (disadvantages) of half-adder:
o In multi-digit addition we have to add two bits along with the carry of previous digit
addition. Such addition requires addition of 3 bits. This is not possible in half-adders.
Full Adder:
o In a full adder, three bits can be added at a time. The third bit is a carry from a less
significant column.
o If the carry from the bit is considered, it is called full add.
o The circuit which performs the full add function is called Full Adder

41. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
A full adder can be made from two half adders (plus an OR gate).

42. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
Half Subtractor: is a combinational circuit that performs subtraction of two bits and has two inputs
and two outputs. The two inputs denoted by A and B represents minuend and subtrahend. The two
outputs are the difference “D” and the borrow bit “Bo“.
Truth Table of a half subtractor circuit can be derived as follows:
A B D Bo
0 0 0 0
0 1 1 1
1 0 1 0
1 1 0 0
From the truth table, Boolean Expression can be derived as:
Full Adder
A B
CC
S
i i
i+1 i
i

43. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
D = A’B + AB’ = A ⊕ B
Bo = A’B
A Half Subtractor circuit can be implemented using AND & OR logic gates or by using XOR, NOT &
AND logic gates. Both these implementations are shown in the image below:
n FULL SUBTRACTORSare logiccomponentsthatdirectlysubtracttwovalues.Ithasthree inputs:twodata
inputsanda borrowinput.
n TWO’s COMPLEMENT can alsobe usedto implementsubtraction.Two’scomplementof avalue isthe
negative of thatvalue.Itis generatedbycomplementingthe value andadding1.

44. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag
MINIMIZATION OF BOOLEAN FUNCTIONS

45. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag

46. Digital Electronics
T.Srikrishna, M.Tech,G.V.P College for Degree and PG Courses ,Vizag