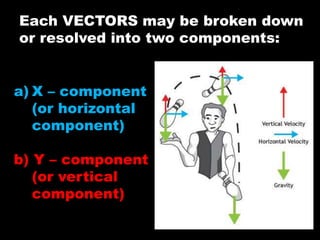
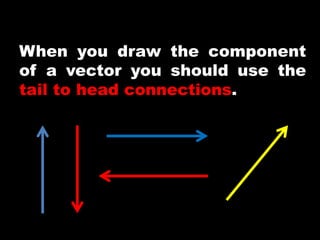
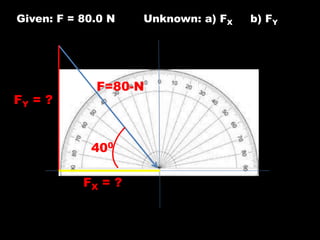
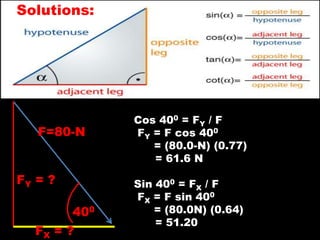
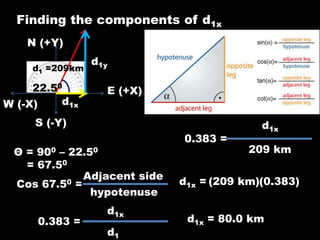
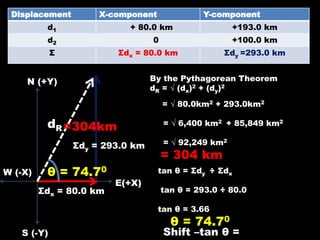
The document explains the components of vectors in two dimensions, describing how to resolve them into x and y components for force, displacement, velocity, and acceleration. It includes examples of calculating these components using trigonometric functions and provides practice exercises related to vector components and resultant velocities. A detailed calculation is illustrated with an airplane's journey and force applications on objects.

1. Components of Vectors
Prepared by:
Victor Rea Oribe

2. Components of a Vector
Motion in two dimensions can
be described by using VECTORS
such as:
a) FORCE (F)
b) DISPLACEMENT (d)
c) VELOCITY (v)
d) ACCELERATION (a)

3. Each VECTORS may be broken down
or resolved into two components:
a) X – component
(or horizontal
component)
b) Y – component
(or vertical
component)

5. Vector X-
component
Y-
component
Force, F FX FY
Displacement , d dx dy
Velocity , v vx vy
Acceleration, a ax ay
Representation of Component
vectors

6. The magnitude and direction of the
components of a vector may be
found using the concepts of:
a) rectangular
coordinate
system

7. b) Trigonometric functions

8. When you draw the component
of a vector you should use the
tail to head connections.

9. Example:
A force of 80.0 N is applied y a janitor on
the handle of a mop held at 400 angle with
the floor. What force is pushing the mop
(a) across the floor and (b) downward to
the floor
Given:
F = 80.0 N θ = 400
Unknown:
FX = force that pushes the mop across the floor
FY = force that pushes the mop downward on the
floor.

10. Given: F = 80.0 N Unknown: a) FX b) FY
400
F=80-N
FY = ?
FX = ?

11. Solutions:
400
F=80-N
FY = ?
FX = ?
Cos 400 = FY / F
FY = F cos 400
= (80.0-N) (0.77)
= 61.6 N
Sin 400 = FX / F
FX = F sin 400
= (80.0N) (0.64)
= 51.20

12. An airplane travels 209 km on a straight
course at an angle of 22.50 east of north.
It then changes its course by moving 100
km north before reaching its destination.
Determine the resultant displacement of
the airplane.
Given: (a) d1=209km, 22.5EN (b) d2=100km,N (c) dR
Vector diagram:
N (+Y)
S (-Y)
W (-X)
E (+X)
22.50
N (+Y)
S (-Y)
W (-X) E (+X)
d2 100 km

13. Finding the components of d1x
N (+Y)
S (-Y)
W (-X)
E (+X)
d1 =209km
22.50
d1x
d1y
Θ = 900 – 22.50
= 67.50
Cos 67.50 =
Adjacent side
hypotenuse
0.383 =
d1x
d1
0.383 =
d1x
209 km
d1x = (209 km)(0.383)
d1x = 80.0 km

14. Finding the components of d1y
N (+Y)
S (-Y)
W (-X)
E (+X)
d1 =209km
22.50
d1y =193km
d1y = ?
Θ = 900 – 22.50
= 67.50
sin 67.50 =
opposite side
hypotenuse
0.924 =
d1y
d1
0.924 =
d1y
209 km
d1y = (209 km)(0.924)
d1y = 193 km
d1x = ?

15. N (+Y)
E (+X)
d1 =209km
22.50
d1x = 80.0km
d1y =193.0km
Finding the components
of d2 N (+Y)
S (-Y)
E (+X)W (-X)
d2y = 100.0km
Displacement X-component Y-component
d1 + 80.0 km +193.0 km
d2 0 +100.0 km
Σ Σdx = 80.0 km Σdy =293.0 km

16. Displacement X-component Y-component
d1 + 80.0 km +193.0 km
d2 0 +100.0 km
Σ Σdx = 80.0 km Σdy =293.0 km
N (+Y)
S (-Y)
W (-X)
E(+X)
Σdx = 80.0 km
Σdy = 293.0 km
dR
By the Pythagorean Theorem
dR = √ (dx)2 + (dy)2
= √ 80.0km2 + 293.0km2
= √ 6,400 km2 + 85,849 km2
= √ 92,249 km2
= 304 km
=304km
θ = 74.70 tan θ = Σdy ÷ Σdx
tan θ = 293.0 ÷ 80.0
tan θ = 3.66
θ = 74.70
Shift –tan θ =

17. Practice Exercise
1. A man exerts a force of 200 N on a
wheelbarrow at an angle of 300 above the
horizontal. What are the horizontal and
vertical forces exerted on the handle of the
wheelbarrow?
2. A`plane flying due north at 100m/s is blown by
a 50 m/s strong wind due east.
a. Draw a diagram to illustrate the problem
b. What is the plane’s resultant velocity?
3. Find the components of the following vectors
(present the data in tabular form)
a. The initial velocity of a golf is 10 m/s, 320
north of west.
b. A force of 120 N pulls a loaded box 400
south of west.