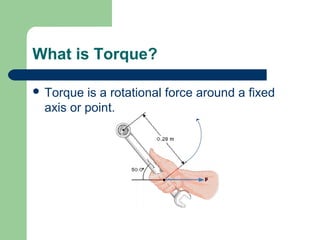
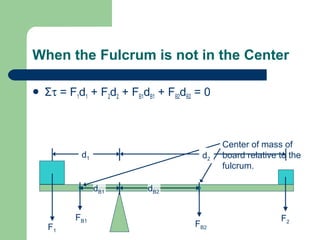
Torque is a rotational force that depends on three main factors: the distance from the axis of rotation (lever arm), the angle of the applied force, and the magnitude of the applied force. Torque causes an object to rotate and is measured in Newton-meters. Systems in rotational equilibrium have no net torque, meaning the sum of all torques acting on the object is zero. This allows seesaws and diving boards to remain balanced. Solving rotational equilibrium problems involves drawing free body diagrams and setting the sum of torques equal to zero.

1. Torque
Chapter 9 – Rotational
Dynamics

2. What is Torque?
 Torque is a rotational force around a fixed
axis or point.

3. Torque
 Torque is represented using the Greek letter
tau as follows:
τ = Fd sinθ
-Where
F = Force (Newtons)
d = lever arm length
θ = angle that force makes with the
axis of the lever arm
Note: Torque is a vector quantity.

4. Factors that affect Torque
 Distance: The distance from the point of rotation affects
torque in such a manner that the further you are from the
axis of rotation, the easier it is to rotate around that point.
F1
F2
d2
d1
Note: The distance d is also known as the lever arm.

5. Factors that affect Torque
 Angle: Torque also depends on the angle at which the
force makes with the lever arm. Torque is maximum
when the force makes a 90° angle with the lever arm.
d
F
θ
θ

6. Factors that affect Torque
 Force: Torque is directly proportional to the force
applied to the lever arm. As the force increases, so
does the torque.
F1
d
F2
d
F2 > F1
τ2 > τ1

7. Torque & Seesaws
 Equilibrium: Equilibrium exits when the seesaw is
balanced such that it will not tend to rotate around
the fulcrum.
– At Equilibrium:
 There is no net torque
 There is no net force.
Fulcrum

8. Conditions for Equilibrium
1. The sum of the forces must equal zero.
– ΣF = F1 + F2 – FF = 0
– ΣF = m1g + m2g – FF = 0
1. The sum of the torques must equal zero.
– Στ = F1d1 + F2d2 = 0

9. Translational Equilibrium
 The sum of the forces must equal zero.
– ΣF = F1 + F2 – FF = 0
– ΣF = m1g + m2g – FF = 0
F1 F2
FF

10. Rotational Equilibrium
 The sum of the torques must equal zero.
– Στ = F1d1 + F2d2 = 0
– Note that one torque will provide a rotational force in
the counterclockwise direction (F1) while the other
force will provide a rotational force in the clockwise
direction (F2)
F1 F2
d1 d2

11. Center of Mass
 If the fulcrum (pivot point) does not occur at
the center of the object, then the center of
mass must be factored into the problem.
 For uniform geometric shapes, the center of
mass can be conveniently chosen at the
center of the object.
Center of Mass

12. When the Fulcrum is not in the Center
 Στ = F1d1 + F2d2 + FB1dB1 + FB2dB2 = 0
F1
F2
Center of mass of
board relative to the
fulcrum.
FB1
FB2
d1
dB1 dB2
d2

13. Solving Problems involving Torque
1. Select the object to which the equations for equilibrium are to
be applied.
2. Draw a free-body diagram that shows all of the external
forces acting on the object.
3. Choose a convenient set of x, y axes and resolve all forces
into components that lie along these axes.
4. Apply the equations that specify the balance of forces at
equilibrium. (Set the net force in the x and y directions equal
to zero.)
5. Select a convenient axis of rotation. Set the sum of the
torques about this axis equal to zero.
6. Solve the equations for the desired unknown quantities.

14. A woman whose weight is 530 N is
poised at the right end of a diving board
with length 3.90 m. The board has
negligible weight and is supported by
a fulcrum 1.40 m away from the left
end.
Find the forces that the bolt and the
fulcrum exert on the board.
Example 1: A Diving
Board

15. 022 =−=∑ WWF τ
( )( ) N1480
m1.40
m90.3N530
2 ==F
2
2

WW
F =
Example 1: A Diving
Board

16. 021 =−+−=∑ WFFFy
0N530N14801 =−+− F
N9501 =F
Example 1: A Diving
Board

17. Torque Applied to Mobiles
 The mobile can be looked at as a balance of
forces in motion.
 The forces of nature – wind and gravity –
play a significant role in understanding how
mobiles function.

18. Torque and Mobiles
FM
FE
FS
Στ = 0