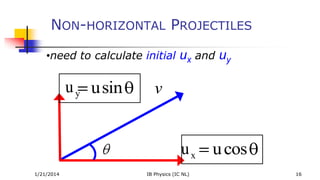
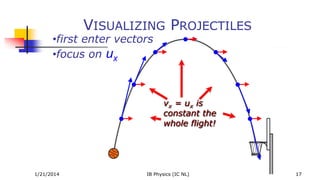
This document discusses projectile motion, beginning with an overview of the objectives and definitions. It explains that a projectile experiences only gravity and air resistance, and its motion can be analyzed as independent vertical and horizontal components. Horizontal projectiles follow the simplest case where velocity is constant horizontally but follows parabolic free fall vertically. Non-horizontal projectiles require calculating initial velocity components and analyzing changes in vertical velocity over time. Solving projectile motion problems generally involves drawing diagrams, choosing a coordinate system, and applying the independent kinematic equations along each axis. Air resistance decreases a projectile's range from the ideal parabolic trajectory.

1. PROJECTILE MOTION
1/21/2014
IB Physics (IC NL)
1

2. Projectile Motion
Motion in Two Dimension
1/21/2014
IB Physics (IC NL)
2

3. Topic objectives





State the independence of the vertical and the horizontal
components of velocity for a projectile in a uniform field.
Describe and sketch the trajectory of projectile motion as
parabolic in the absence of air resistance.
Describe qualitatively the effect of air resistance on the
trajectory of a projectile.
Solve problems on projectile motion.
Remarks:
1. Proof of the parabolic nature of the trajectory is not required.
2. Problems may involve projectiles launched horizontally or at any angle above or below the
horizontal. Applying conservation of energy may provide a simpler solution to some problems
than using projectile motion kinematics equations.
1/21/2014
IB Physics (IC NL)
3

4. What is a projectile?



1/21/2014
When a body is in free motion, (moving
through the air without any forces apart
from gravity and air resistance), it is called a
projectile
Normally air resistance is ignored so the only
force acting on the object is the force due to
gravity
This is a uniform force acting downwards
IB Physics (IC NL)
4

5. Types of projectiles
There are three types of projectile depending on
the value of the angle between the initial velocity
and the x-axis.
1. θ = 0
horizontal projectile
2. θ = 90 vertical projectile (studied earlier)
3. θ = θ which is the general case.
1/21/2014
IB Physics (IC NL)
5

6. HORIZONTAL PROJECTILES
•Horizontal Projectiles are easiest to work
with
•only formula used in horizontal (x)
direction is:
x = ut
Remark: in case of horizontal
projectiles select the direction
of the y-axis to be downward.
1/21/2014
IB Physics (IC NL)
6

7. HORIZONTAL PROJECTILES
•Horizontal Projectiles are the most basic
•only formula used in horizontal (x)
direction is:
x = ut
constant speed!
1/21/2014
IB Physics (IC NL)
7

8. HORIZONTAL PROJECTILES
•vertical (y) direction is just freefall
•all of the initial velocity is in the x
direction
•So,
u
t1
t2
t3
t4
1/21/2014
IB Physics (IC NL)
8

9. EXAMPLE
A person decides to fire a rifle horizontally at a
bull’s-eye. The speed of the bullet as it leaves the
barrel of the gun is 890 m.s-1. He’s new to the
ideas of projectile motion so doesn’t aim high and
the bullet strikes the target 1.7 cm below the
center of the bull’s-eye.
What is the horizontal distance between the rifle
and the bull’s-eye?
start by drawing a picture:
label the explicit givens
890 m.s
1
1.7 cm
1/21/2014
IB Physics (IC NL)
9

10. EXAMPLE
What is the horizontal distance between the rifle
and the bull’s-eye?
X
ux
890 m.s
Y
1
y
ay
uy
1.7 cm
m
9.8 2
s 1
0 m.s
890 m.s
1m
100cm
0.017m
1
1.7 cm
want:
1/21/2014
dx
horizontal distance
IB Physics (IC NL)
10

11. EXAMPLE
which equation do we use?
use
y
0
1 2
ayt uyt
2
to find time
rewrite equation for t
t
1/21/2014
2y
ay
2(0.017)
9.8
IB Physics (IC NL)
0.059 s
11

12. EXAMPLE
Use t and ux to solve for x
x
1/21/2014
uxt
(890)(0.059)
IB Physics (IC NL)
52.4 m
12

13. 1/21/2014
IB Physics (IC NL)
13

14. NON-HORIZONTAL PROJECTILES
• vx = ux is still constant
• uy is also constant
•only difference with non-horizontal is
that vy is a function of time
u
1/21/2014
IB Physics (IC NL)
14

15. NON-HORIZONTAL PROJECTILES
•Angled Projectiles require a little work
to get useful u
•u has an x and y component
•need to calculate initial ux and uy
u
1/21/2014
IB Physics (IC NL)
15

16. NON-HORIZONTAL PROJECTILES
•need to calculate initial
u y usin
ux and uy
v
ux
1/21/2014
IB Physics (IC NL)
u cos
16

17. VISUALIZING PROJECTILES
•first enter vectors
•focus on ux
vx = ux is
constant the
whole flight!
1/21/2014
IB Physics (IC NL)
17

18. VISUALIZING PROJECTILES
•first enter vectors
•focus on vx
•focus on vy
no vy at the top!
vy decreases as it
rises!
by how much per second?
1/21/2014
IB Physics (IC NL)
18

19. VISUALIZING PROJECTILES
1/21/2014
IB Physics (IC NL)
19

20. Boundary conditions: at t = 0, x0 = y0 = 0
ux = ucosθ and uy = usinθ
1/21/2014
IB Physics (IC NL)
20

21. Mathematical analysis

1/21/2014
IB Physics (IC NL)
21

22. Importance of time
Whatever you need to calculate look for time which is common for x and y

1/21/2014
IB Physics (IC NL)
22

23. LET’S
1/21/2014
ANALYZE THE JUMP
IB Physics (IC NL)
23

24. VARIED ANGLES
•which projectile angle shoots highest?
•larger θ means faster uy
•which projectile angle shoots farthest?
•45° has perfect balance of fast vx and long flight
time.
1/21/2014
IB Physics (IC NL)
24

25. If projectiles are launched at the same speed, but at different
angles, the height and range is of the projectile are affected.
1/21/2014
IB Physics (IC NL)
25

27. Solving Problems Involving Projectile
Motion
1. Read the problem carefully, and choose the
object(s) you are going to analyze.
2. Draw a diagram.
3. Choose an origin and a coordinate system.
4. Decide on the time interval; this is the same in
both directions, and includes only the time the
object is moving with constant acceleration g.
5.Examine the x and y motions separately.

28. Solving Problems Involving Projectile
Motion (cont.)
6. List known and unknown quantities.
Remember that vx never changes, and that
vy = 0 at the highest point.
7. Plan how you will proceed. Use the
appropriate equations; you may have to
combine some of them.
1/21/2014
IB Physics (IC NL)
28

29. When the effect of air resistance is significant,
the range of a projectile is diminished and the
path is not a true parabola.
22

30. In the case of air resistance, the path of a high-speed
projectile falls below the idealized path and follows
the solid curve.
Computer-generated trajectories of a baseball with and
without drag.
23