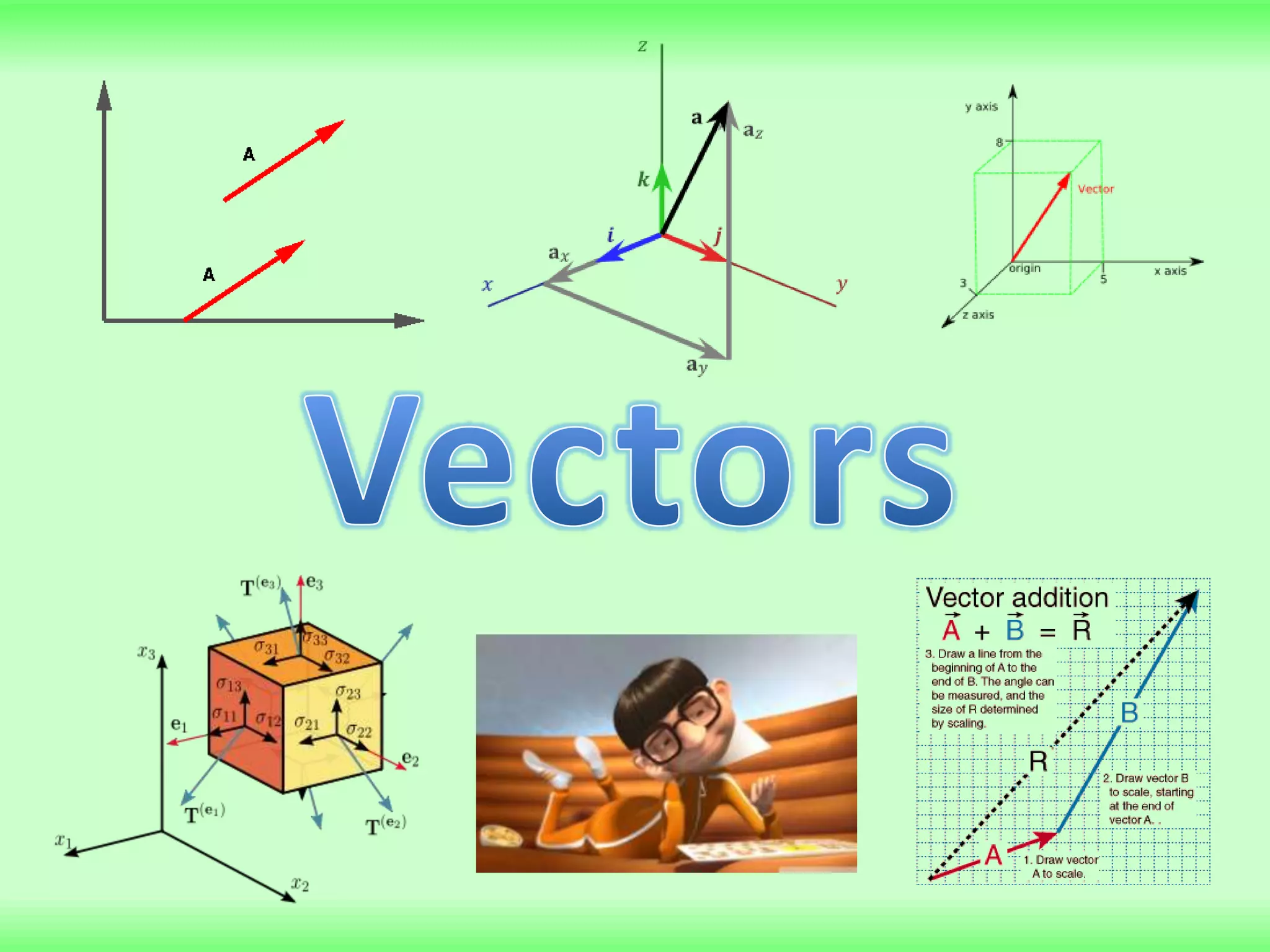
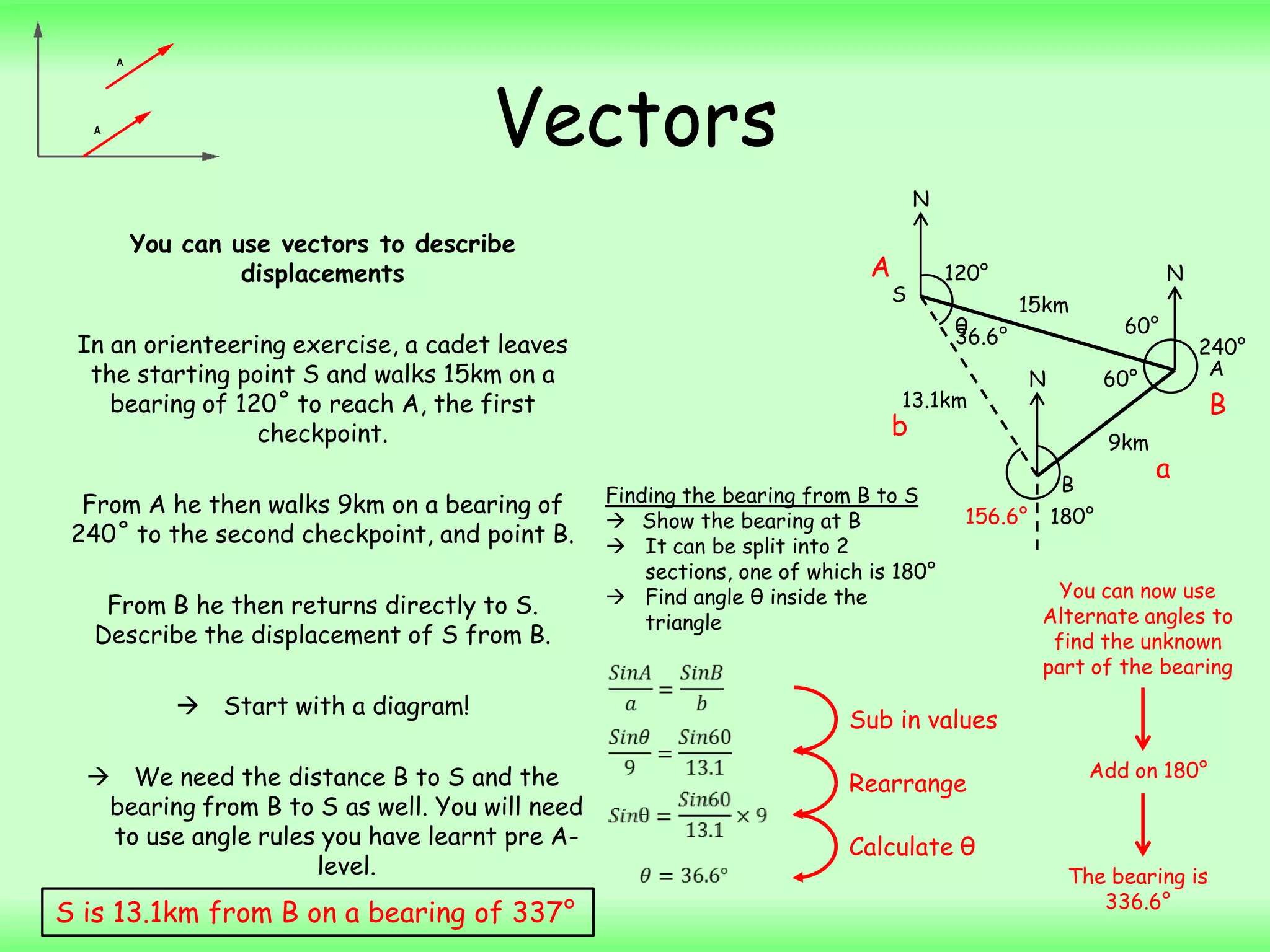
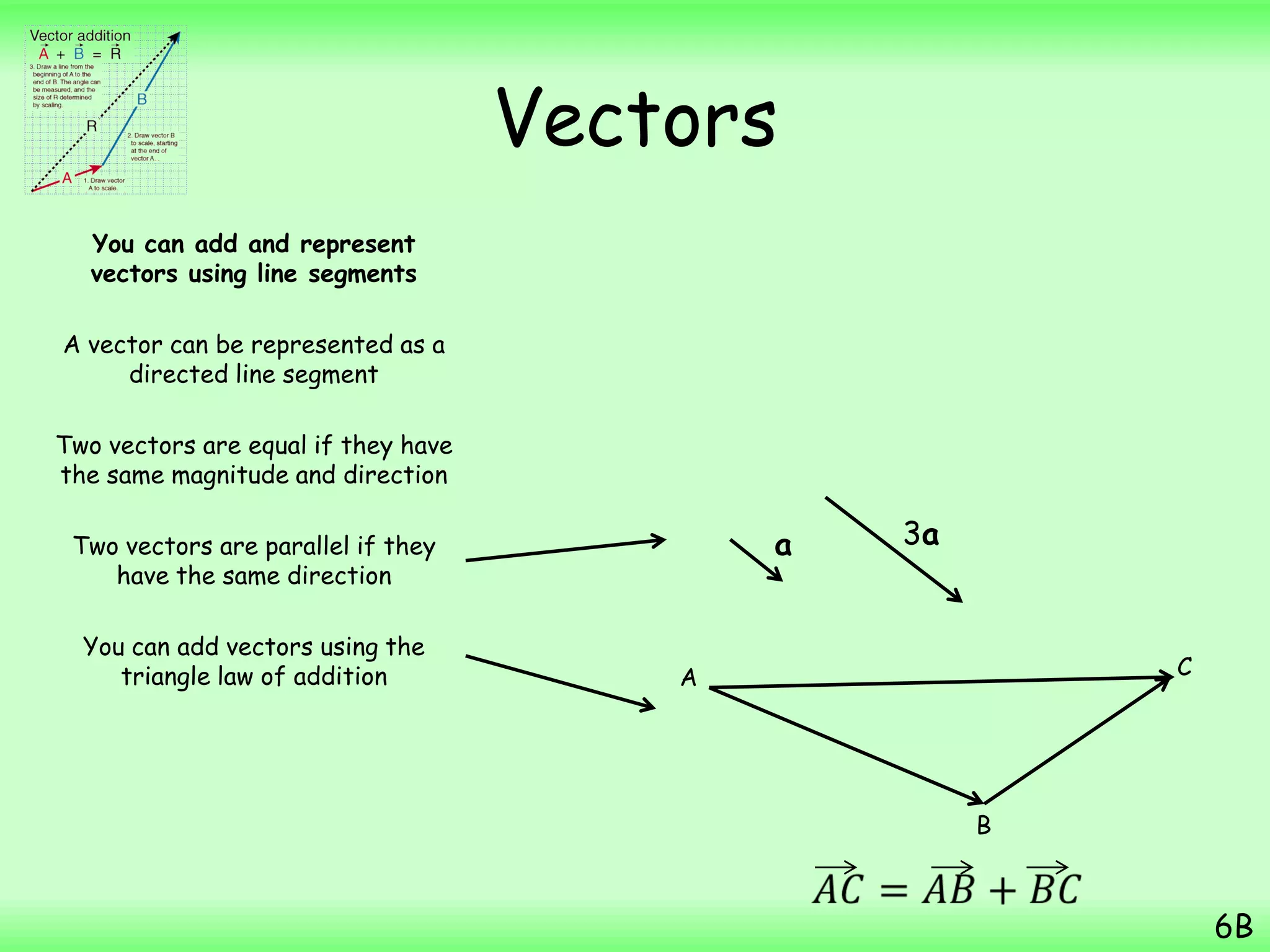
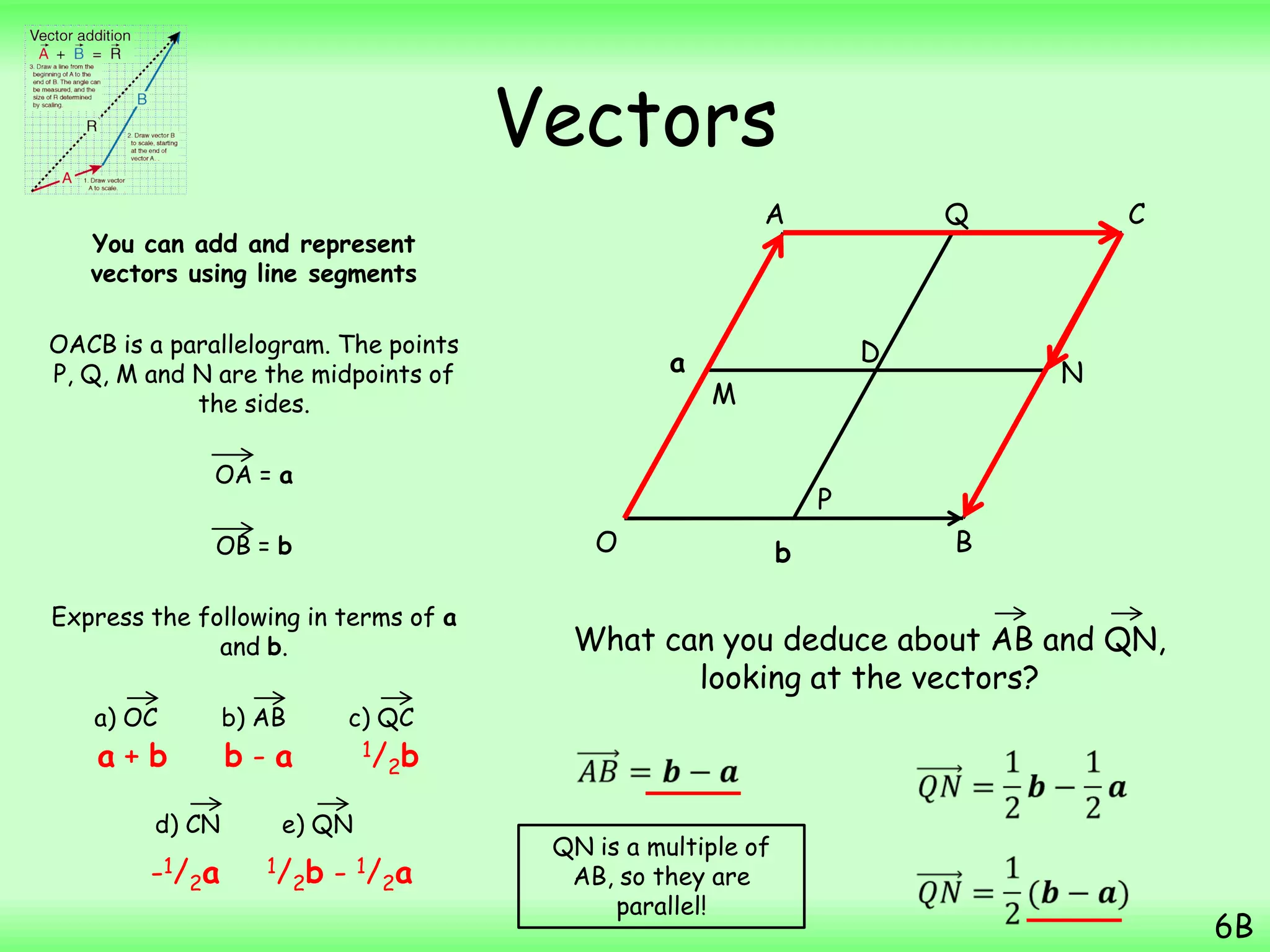
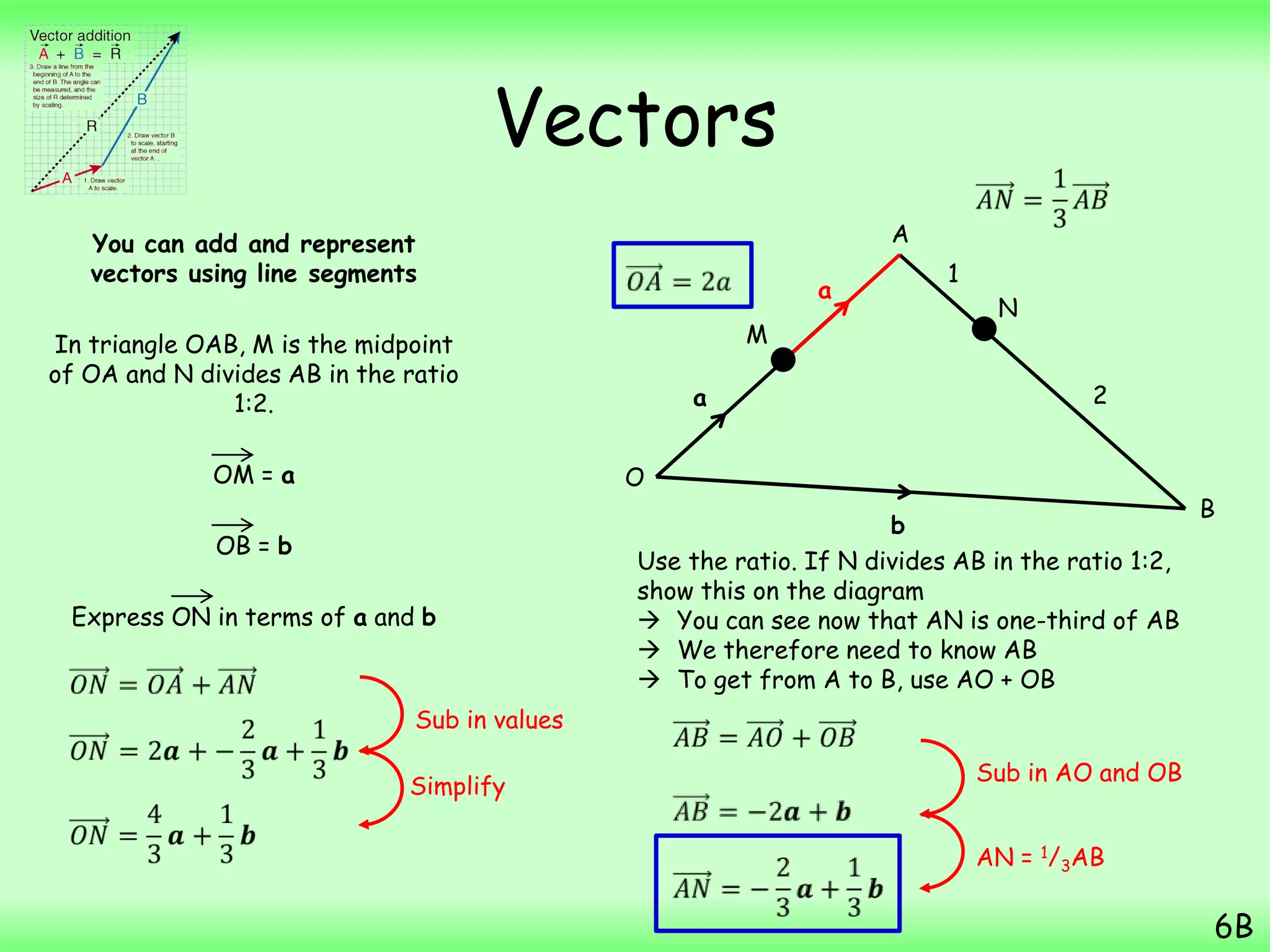
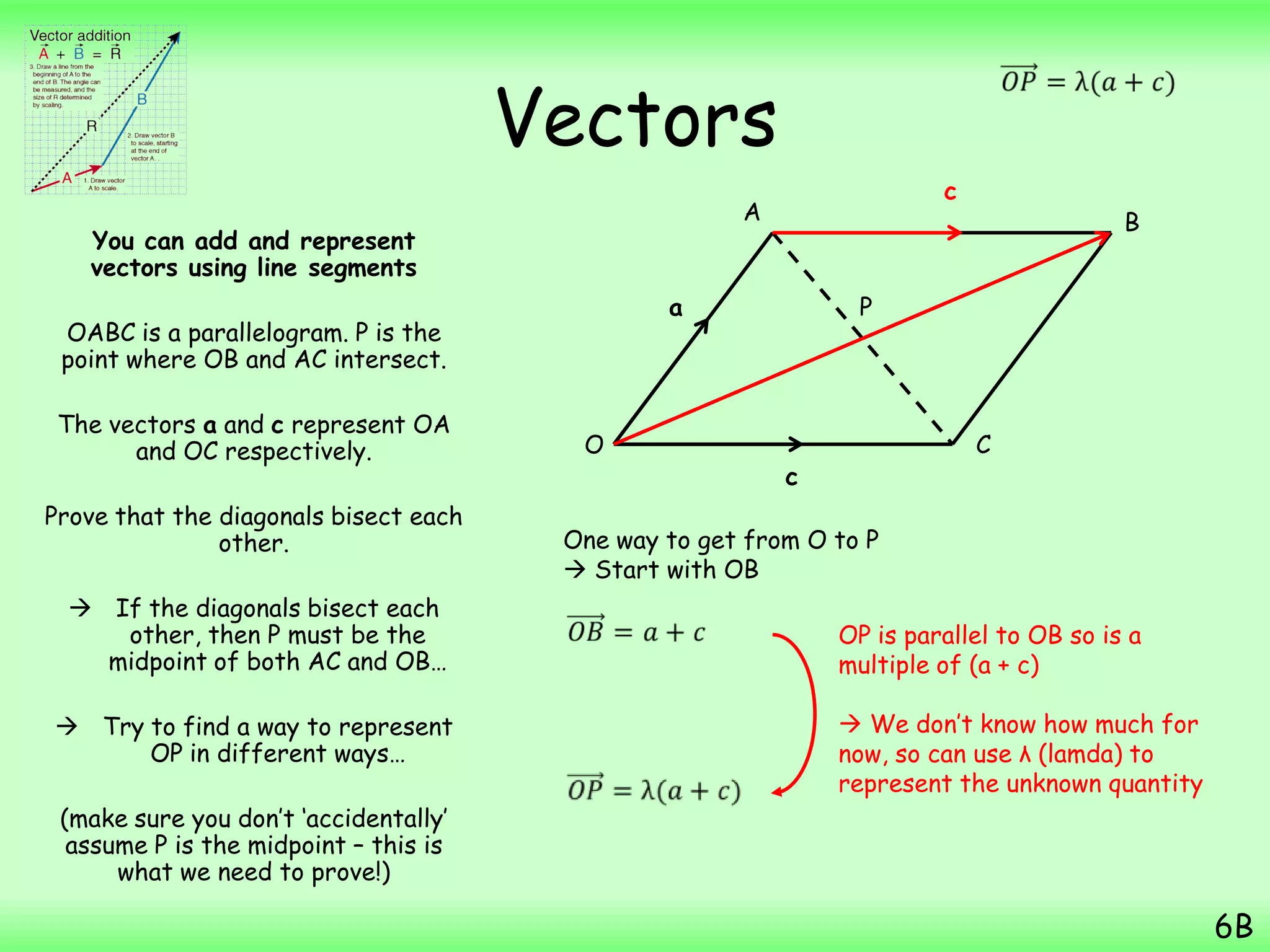
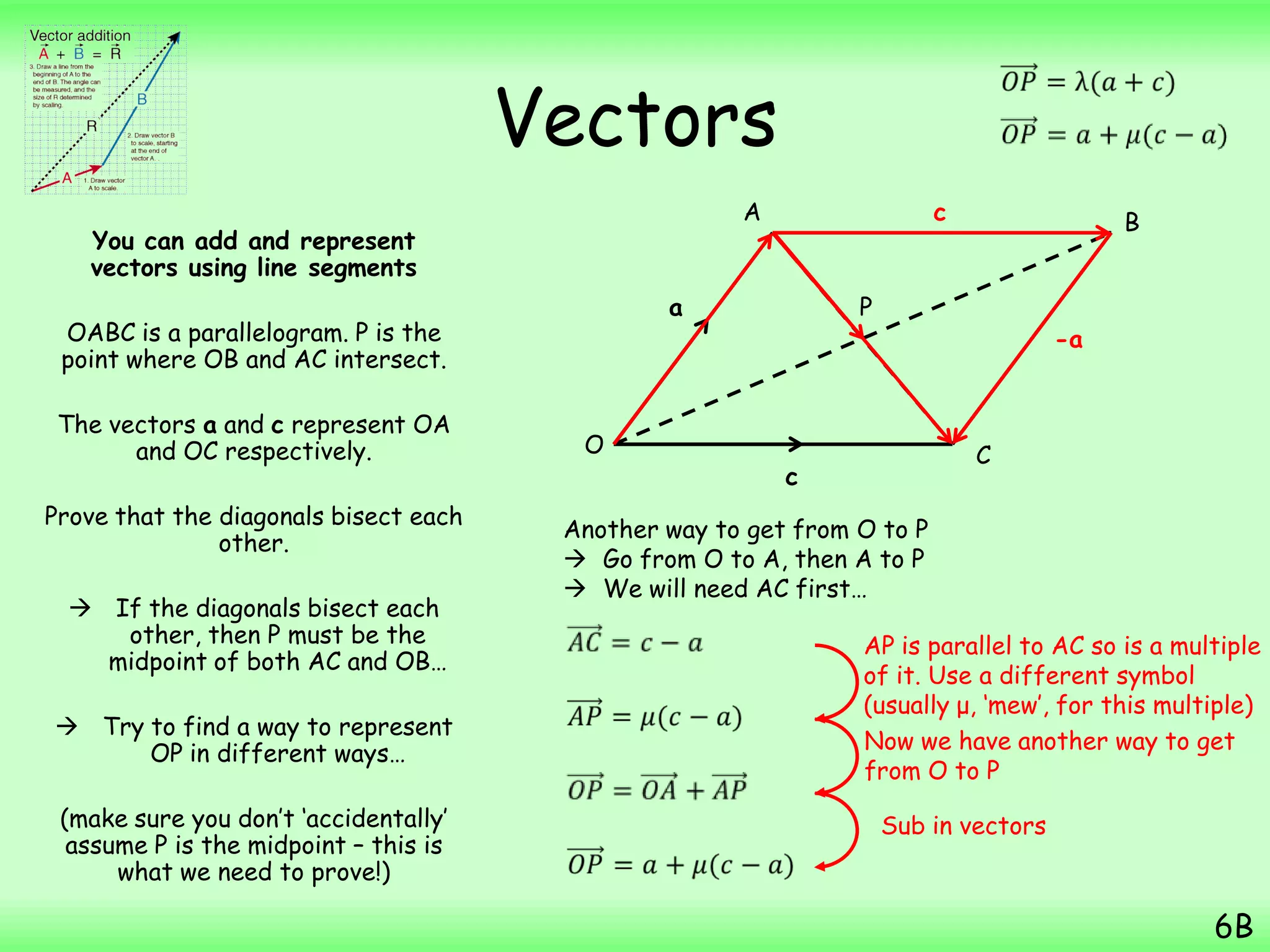
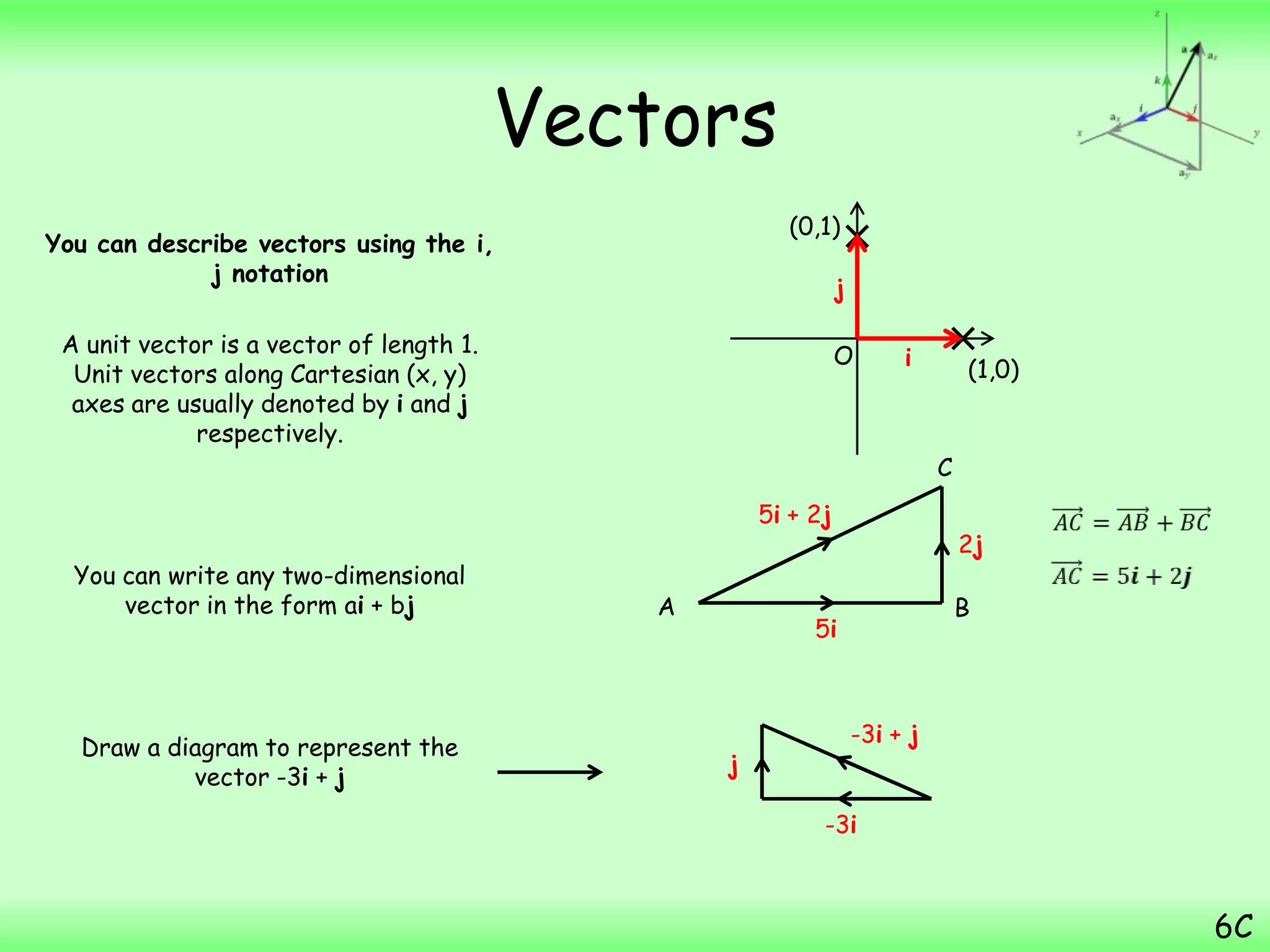
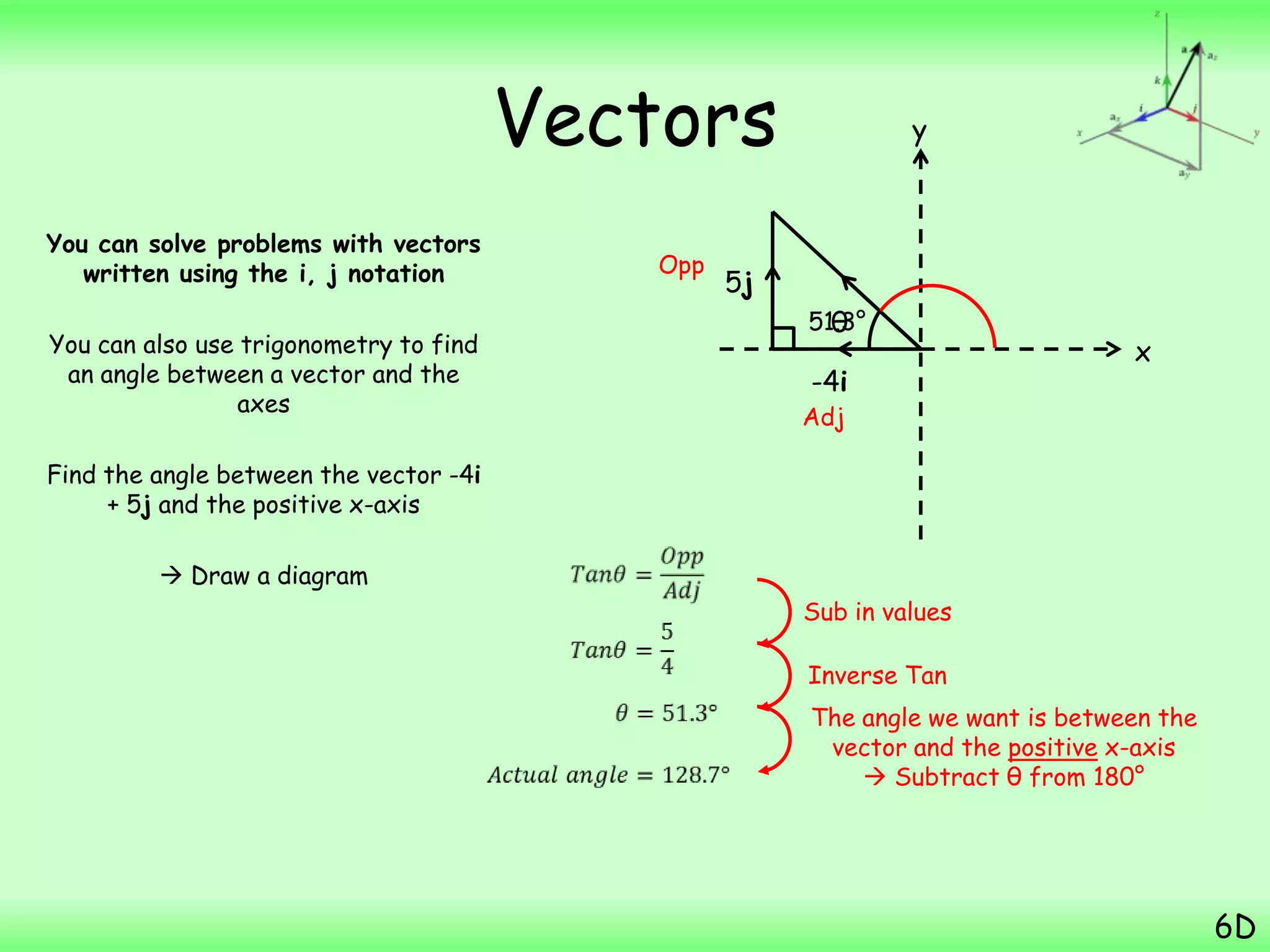
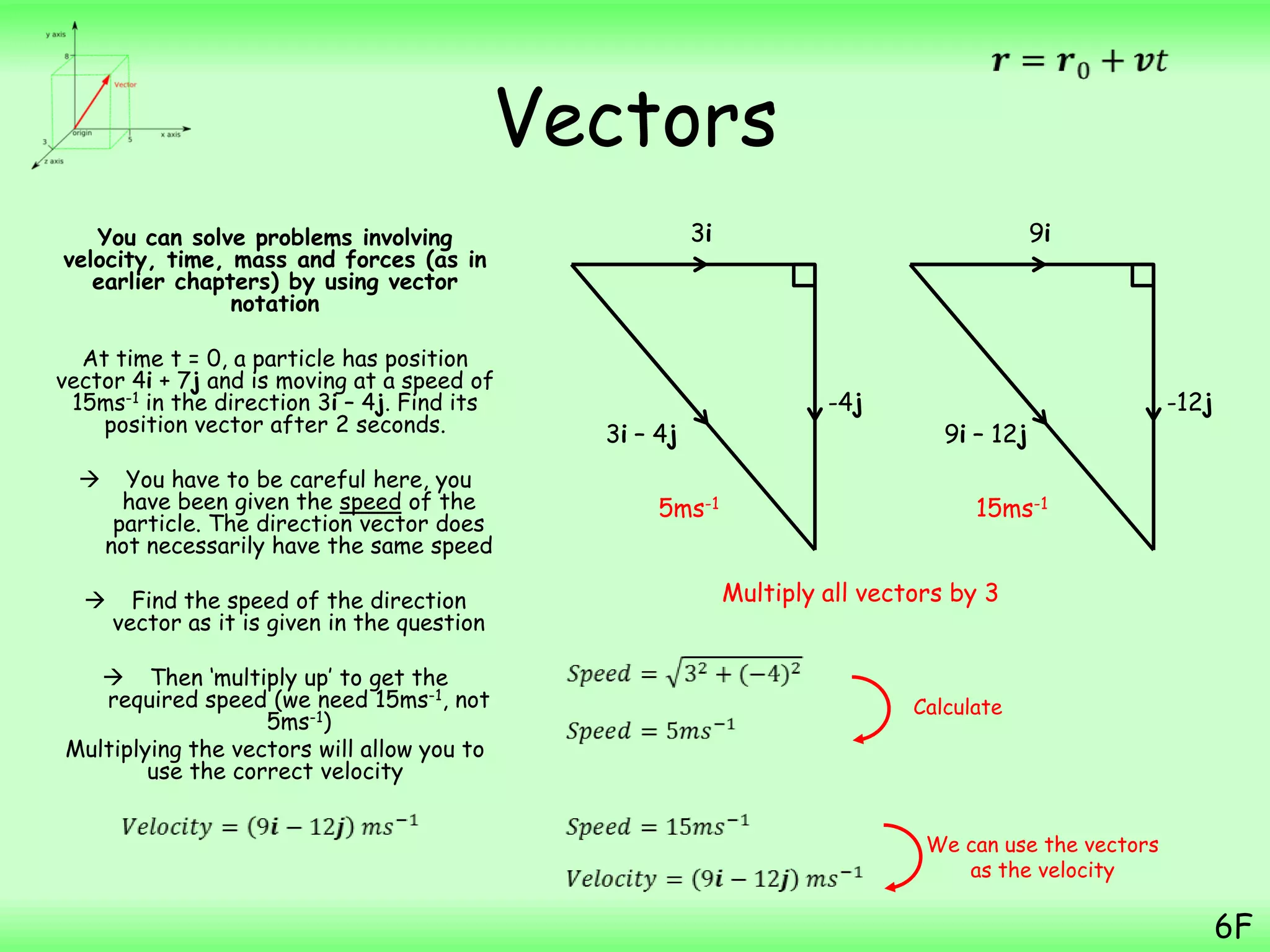
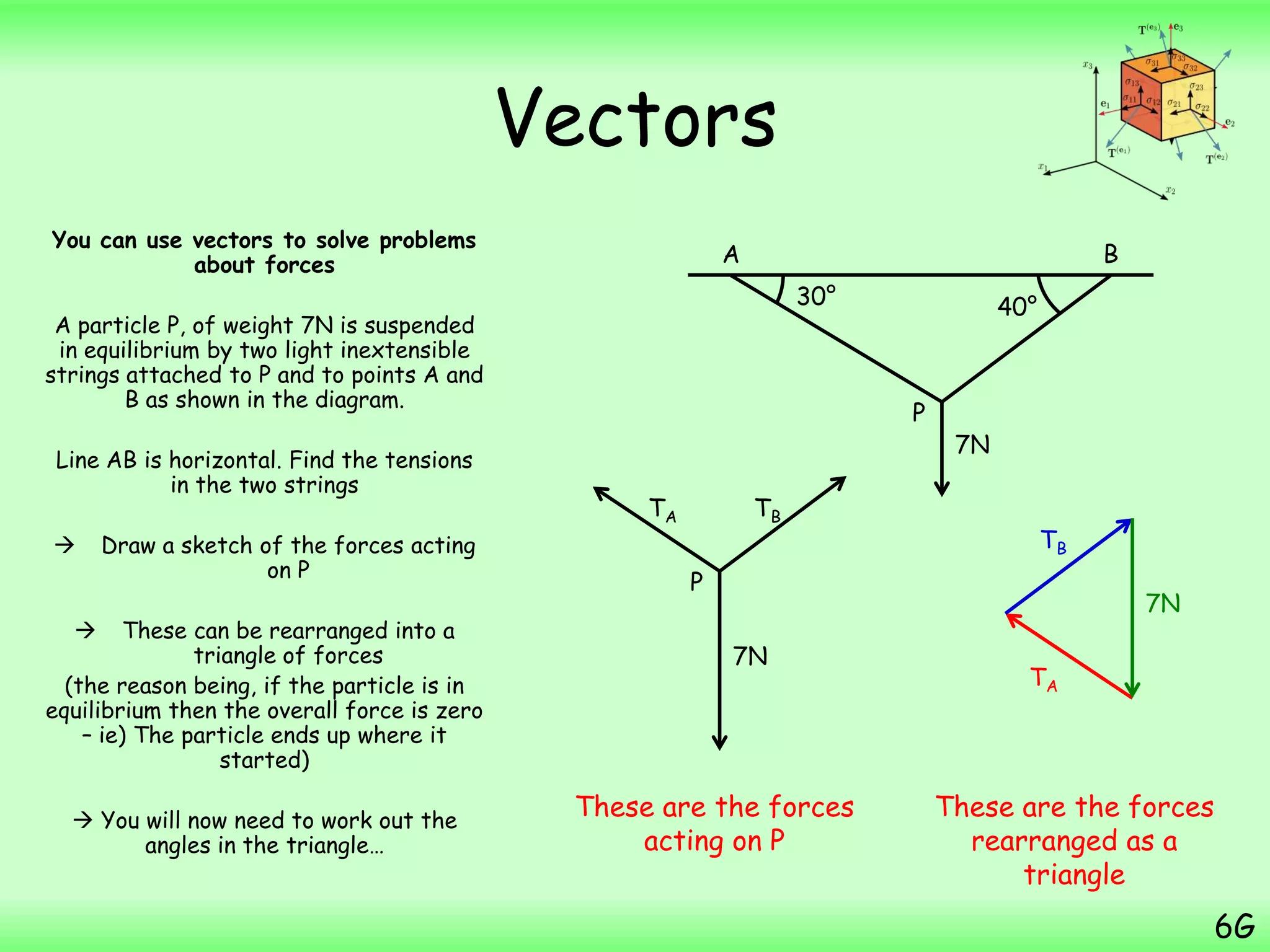
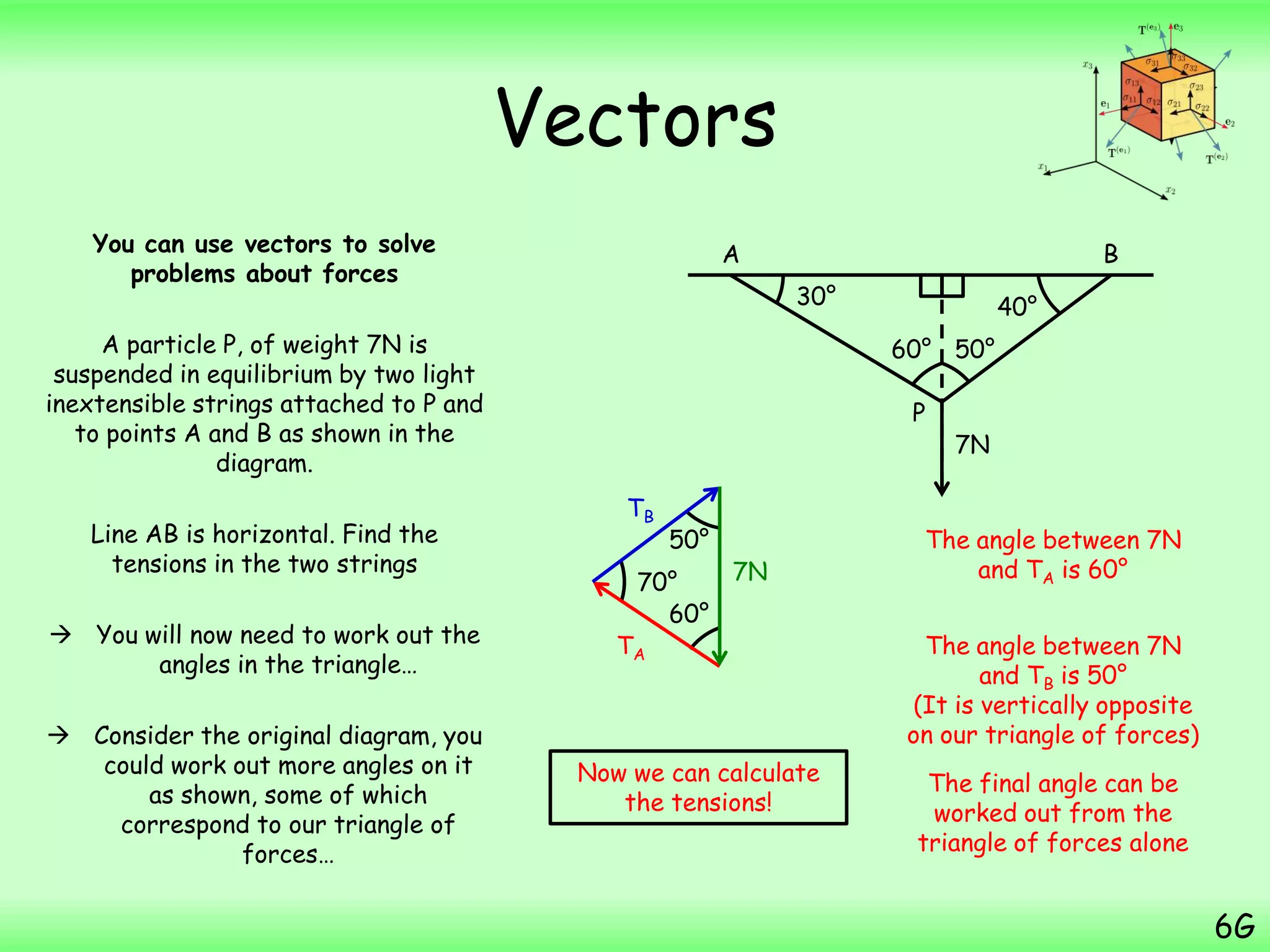
- A particle starts from the point with position vector (3i + 7j) m and then moves with constant velocity (2i – j) ms-1. The question asks to find the position vector of the particle 4 seconds later.
- Substituting the values into the displacement equation gives the final position vector as (12i + 3j) m.
- A second particle is given a position vector of (2i + 4j) m at time t = 0 and a position vector of (12i + 16j) m five seconds later. Using the displacement equation gives the velocity of the particle as (2i + 4j) ms-1.
- For a third particle