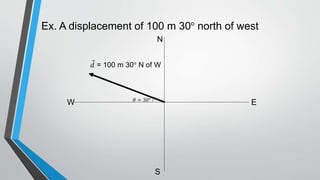
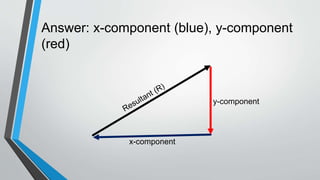
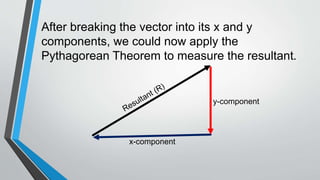
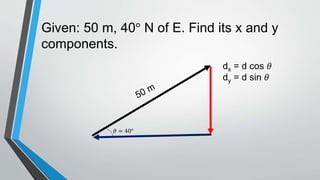
The document covers lesson 6.3 on vector representation, exploring concepts such as scalar and vector quantities, different methods of vector addition (graphical, mathematical, and component methods), and the Pythagorean theorem. It provides examples of representing vectors in various scenarios and offers a procedural explanation for calculating resultant vectors, especially when dealing with non-right-angle vectors. It concludes with an assignment requiring students to apply these concepts to real-world navigation problems.

1. VectorsUnit SIX, Lesson 6.3
By Margielene D. Judan

2. LESSON OUTLINE
Vector Representation
Graphical Method
Mathematical Method
PythagoreanTheorem
Component Method

3. Various quantities in nature can be:
• Scalar quantity – magnitude only
• Vector quantity – magnitude + direction

4. The length of the arrow represents the
magnitude while the angle where the arrow is
pointed represents the direction.

5. Thus, a longer vector has a larger
magnitude.
A B C
Which among the vectors has the largest magnitude?

6. Examples of Vector Representation:
• 30 km/hr East
• 20 km/hr West
• 10 km/hr North
30 km
20 km
10 km

7. Examples of Vector Representation:
• 50 km/hr NE
• 50 km/hr SE
50 km
50 km

8. Vectors can also be drawn in a Cartesian
coordinate system.
West
North
East
South

9. Ex. A force of 80 Newtons east
𝐹 = 80 N east
W
N
E
S

10. Ex. A velocity of 120 km/hr southwest
𝑣 = 120 km/hr SW
𝜃 = 45°
W
N
E
S

11. Ex. A displacement of 100 m 30° north of west
𝑑 = 100 m 30° N of W
𝜃 = 30°
W
N
E
S

12. We use a protractor to measure the angles in
degrees, and a ruler to measure the magnitude.

13. Vector Addition

14. We can add vectors using different
methods. The sum of the vectors (vector
sum) is called the resultant vector,
denoted by R.

15. Vector Addition Methods
• Graphical Method or the Tip-to-Tail Method
• Mathematical Method
1. Pythagorean Theorem
2. Component Method

16. 1. Graphical Method or
Tip-to-Tail Method

17. Tip-to-Tail Method
Arrow 1 Arrow 2
Review from Lesson 6.1

18. It is called tip-to-tail because you
connect the arrows from tip to tail
Correct Wrong
tip
tail
tail
tiptip
tail
tail
tail
tail
tip
tip
tip

20. We can use many arrows.

21. 2. Mathematical Method

22. Look at the red line. Can you measure its
exact length?

23. Using the graphical method is easy and
convenient. However, it does not predict
measurements exactly. You cannot
measure 62.5213° on a protractor and
2.617 cm in a ruler exactly.
Thus, we use a more exact method called
the mathematical method.

24. Note:
Right and Up (+)
Left and Down (-)

25. Note:
Right and Up (+)
Left and Down (-)

26. 3. Pythagorean Theorem

27. Note: The Pythagorean Theorem is used
for determining the resultant of two vectors
that makes a right angle to each other.
The formula is given below:

29. Use the Pythagorean Theorem to
determine the resultant vector below.

30. Practice A Solution:
𝑅 = 𝑎2 + 𝑏2
𝑅 = 52 + 102
𝑅 = 25 + 100
𝑅 = 125
𝑹 = 𝟏𝟏. 𝟏𝟖 𝒌𝒎

31. Practice B Solution:
𝑅 = 𝑎2 + 𝑏2
𝑅 = 302 + 402
𝑅 = 900 + 1600
𝑅 = 2500
𝑹 = 𝟓𝟎 𝒌𝒎

32. Assignment
Answer Laboratory 3.2.

33. 4. Component Method

34. Most of the times, the vectors given do not
form right angles and the Pythagorean
Theorem is not applicable.
Pythagorean Theorem
applicable
Pythagorean Theorem
not applicable

35. The Component Method is the best method
to use in all vector problems which vectors
do not form a right angle (Pythagorean
Theorem).
Using this method, vectors are broken
down into its x and y components.

36. Given the vector (black), find its x and y
components using the graphical method.

37. Answer: x-component (blue), y-component
(red)
x-component
y-component

38. After breaking the vector into its x and y
components, we could now apply the
Pythagorean Theorem to measure the resultant.
x-component
y-component

39. Using the mathematical method, however,
we have to apply concepts in trigonometry.

40. Given: 50 m, 40° N of E. Find its x and y
components.
𝜃 = 40°

41. Given: 50 m, 40° N of E. Find its x and y
components.
𝜃 = 40°
dx – x component
dy – y component

42. Given: 50 m, 40° N of E. Find its x and y
components.
𝜃 = 40°
dx = d cos 𝜃
dy = d sin 𝜃

43. Given: 50 m, 40° N of E. Find its x and y
components.
𝜃 = 40°
dx = d cos 𝜃
dx = 50 cos 40°
dx = 38.30 m
dy = d sin 𝜃
dy = 50 sin 40°
dy = 32.14 m

44. Given: 50 m, 40° N of E. Find its x and y
components.
𝜃 = 40°
32.14 m
38.30 m

45. Find the Resultant Using Component
Method (Steps)
1. Make a graphical model of the vectors.
2. Find the x and y components of each vector.
3. Find the sum of all x-components and all y-components.
4. Use the Pythagorean Theorem to find the magnitude of the resultant.
5. Find the direction 𝜃 using tan 𝜃 =
𝑅 𝑦
𝑅 𝑥
.

46. Example:
Arrow 1 = 3 km 30° N of E
Arrow 2 = 4 km 60° S of W

47. 1. Make a graphical model of the vectors.
Arrow 1 = 3 km 30° N
Arrow 2 = 4 km 60° S of W
𝜃 = 30°
𝜃 = 60°
Note:
Right and Up (+)
Left and Down (-)
+y
+x
-y
-x

48. 2. Find the x and y components of each
vector.
Arrow 1
3 km 30° N
Ax = d cos 𝜃
Ax = -3 cos 30°
Ax = -2.60 km
Ay = d sin 𝜃
Ay = -3 sin 30°
Ay = -1.5 km
Arrow 2
4 km 60° S of W
Bx = d cos 𝜃
Bx = 4 cos 60°
Bx = 2 km
By = d sin 𝜃
By = 4 sin 60°
By = 3.46 km
Negative
because x is
to the left
Negative
because y is
downward

49. 3. Find the sum of all x-components and all
y-components.
x-component total Rx = Ax + Bx
= -2.60 km + 2 km
= -0.6 km
y-component total Ry = Ay + By
= -1.5 km + 3.46 km
= 1.96 km

50. 4. Use the Pythagorean Theorem to find
the magnitude of the resultant.
𝑅 = (𝑅 𝑥)2 + (𝑅 𝑦)2
𝑅 = (−0.6)2+1.962
𝑅 = 0.36 + 3.84
𝑅 = 4.2
𝑹 = 𝟐. 𝟎𝟓 𝒌𝒎 (magnitude of resultant)

51. 5. Find the direction 𝜃 using tan 𝜃 =
𝑅 𝑦
𝑅 𝑥
.
tan 𝜃 =
𝑅 𝑦
𝑅 𝑥
tan 𝜃 =
1.96
−0.60
tan 𝜃 = -3.27
To find 𝜃, remove tan by typing tan-1(-3.27) in
the calculator. (teacher will teach you how)
𝜽 = -73.00°

52. Answer: The displacement is
2.05 km, -73.00°
Removing the negative sign:
2.05 km, 73.00° S of E
𝜃 = 73°

53. Whiteboard Work:
Arrow 1 = 20 km 40° S of E
Arrow 2 = 10 km 60° N of E

54. Assignment: (short coupon bond)
From Calapan City Port, the ship travels 15 km, 30° N
of W and 10 km, 10° E of N before reaching Batangas
City Port. Calculate the displacement between the
ports. How far did the ship travel? Make an illustration
by drawing. (30 pts)
Note: Box your final answers.

55. Sources:
Science Links 7