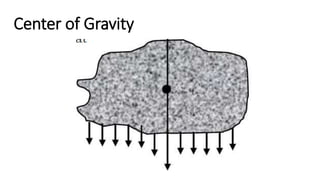
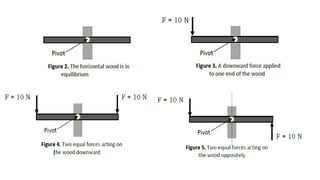
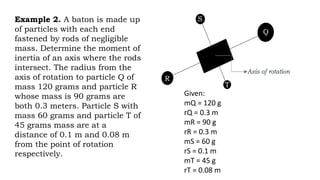
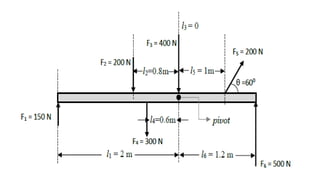
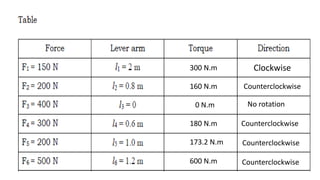
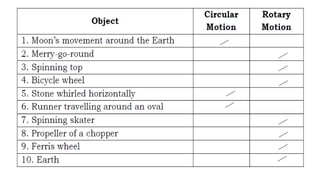
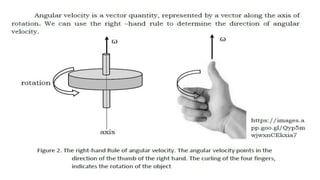
This document provides an overview of torque and moment of inertia for a General Physics 1 course. It defines key concepts like torque, lever arm, and moment of inertia. It gives examples of calculating torque from a force and lever arm and calculating moment of inertia for single and multiple particle systems. The document also previews a future lesson on rotational kinematics that will discuss angular velocity, acceleration, displacement and momentum.

1. GENERAL PHYSICS 1
QUARTER 2, WEEK 1
TORQUE and MOMENT of INERTIA

2. OBJECTIVES:
1. calculate the moment of inertia about a
given axis of single object and multiple-object
systems.
2. calculate magnitude and direction of
torque using the definition of torque as a
cross product.
3. describe rotational quantities under static
equilibrium using vectors.

3. GUIDE QUESTIONS:
1. What is Moment of Inertia?
2. What is Torque?
3. How to calculate moment of inertia and
torque?
4. What are rotational quantities under static
equilibrium?

4. Center of Gravity

5. TORQUE
• Torque is the measure of the turning effect of a rigid
body.
• It is operationally define as the product of a
perpendicular force and the length of its lever arm from
the pivot or axis of rotation.
• Lever arm is a measure of a distance from the force
applied to the pivot
• τ = F.la
where:
τ – torque, expressed in N.m
F – force in newton N
la – lever arm in meter

7. • Torque is a vector quantity.
• The direction of the torque produced by a force is
dependent on the action of the force relative to the
pivot.
• If the force causing the rotation is clockwise,
torque is negative.
• If the force causing rotation is counterclockwise
rotation, then torque is positive.

8. Example 1.
Find the torque produced by the force of 10 N in
Figure 3, if the lever arm is 2 meters.
Given:
F = 10 N
la = 2 m
τ = ?
Solution:
τ = F.la
= (10 N)(2 m)
= 20 N.m

9. Example 2.
If the force in Figure 6 makes an angle of 40°, what is the
torque produced by the force?
Given:
F = 10 N
Ɵ = 40°
la = 2 m
τ = ?
Solution:
τ = (Fcos θ) la
= (10 N)(cos400) (2 m)
= 15.32 N.m

10. MOMENT OF INERTIA
• A rigid body is a solid composed of a collection of particles.
These particles remain static relative to each other and
relative to the axis of rotation. Regardless of the forces
acting on a rigid body, it maintain its original shape and
size.
• Newton’s 1st law of motion as applied to rotating systems
states that, unless hindered by an external force, a rigid
body rotating about a fixed axis will remain rotating at the
same rate within the same axis.
• Moment of inertia is define as the quantity that resists
changes in an object’s rotational state of motion. The
moment of inertia of a point mass is operationally define
by the equation,

11. I = m1r12 + m2r22 + m3r32 + …………

12. Example 1. Find the moment of inertia of a mass 2 kg
rotating at a radius of 0.8 m from the axis of rotation?
Given:
m = 2 kg
r = 0.8 m
I = ?
Solution:
I = m𝑟2
= (2 kg) (0.8 m)2
= 1.28 kg.𝑚2

13. Example 2. A baton is made up
of particles with each end
fastened by rods of negligible
mass. Determine the moment of
inertia of an axis where the rods
intersect. The radius from the
axis of rotation to particle Q of
mass 120 grams and particle R
whose mass is 90 grams are
both 0.3 meters. Particle S with
mass 60 grams and particle T of
45 grams mass are at a
distance of 0.1 m and 0.08 m
from the point of rotation
respectively.
Given:
mQ = 120 g
rQ = 0.3 m
mR = 90 g
rR = 0.3 m
mS = 60 g
rS = 0.1 m
mT = 45 g
rT = 0.08 m

14. SOLUTION:

15. Seatwork: TORQUE
Determine the torque produce in a uniform
bar by a parallel force of 5 000 dynes located
30 cm from the point of rotation.
(1dyne= 1x10−5
N)

16. ACTIVITY:
Refer to Figure, complete the table by
calculating the torque of the uniform bar
and determining the direction caused by
the torque.

18. 300 N.m
160 N.m
0 N.m
180 N.m
173.2 N.m
600 N.m
Clockwise
Counterclockwise
No rotation
Counterclockwise
Counterclockwise
Counterclockwise

19. SEATWORK: MOMENT OF INERTIA
Solve the following:
1. A 30 kg boy is riding on a merry-go-round located 2.5
meters away from the axis of rotation. Determine the
moment of inertia.
2. A 25 kg child is sitting along the rim of a merry-go-
round rotating about its symmetry axis. If the mass of
the merry-go-round is 100 kg and its radius is 8 m,
what is the moment of inertia of the system about its
axis of symmetry. Assuming that the child is treated as
a point particle and the merry-go-round is modelled as
a disc.

20. LESSON 2
ROTATIONAL KINEMATICS

21. OBJECTIVES:
1.apply the rotational kinematic
relations for systems with
constant angular accelerations.
2. determine the angular
momentum of different systems.
3. apply the torque-angular
momentum relation.

23. QUESTIONS:
1. From the table, what is circular
motion?
2. What is rotational motion?

24. • Rotational motion is the
motion of a body about an
internal axis.
• In a circular motion, the axis
of the motion is outside the
object, we call it orbit.
• While rotary motion, the axis
of the motion is inside the
moving object.

25. •In uniform linear motion, velocity is
defined as the time rate of
displacement.
•Similarly, for constant rotary
motion, angular velocity is defined
as the time rate of angular
displacement.
•Angular displacement is the angle
about the axis of rotation through
the object’s turns.
•The angle is measured in radians.

27. Relation between
degrees and radians:
1 revolution = 360° =
2ℼradian
Θ radian = 360°/2𝜋 =
1800/𝜋 = 57.30°
1 radian = 57.30°

28. • Angular velocity can be expressed using the equation,