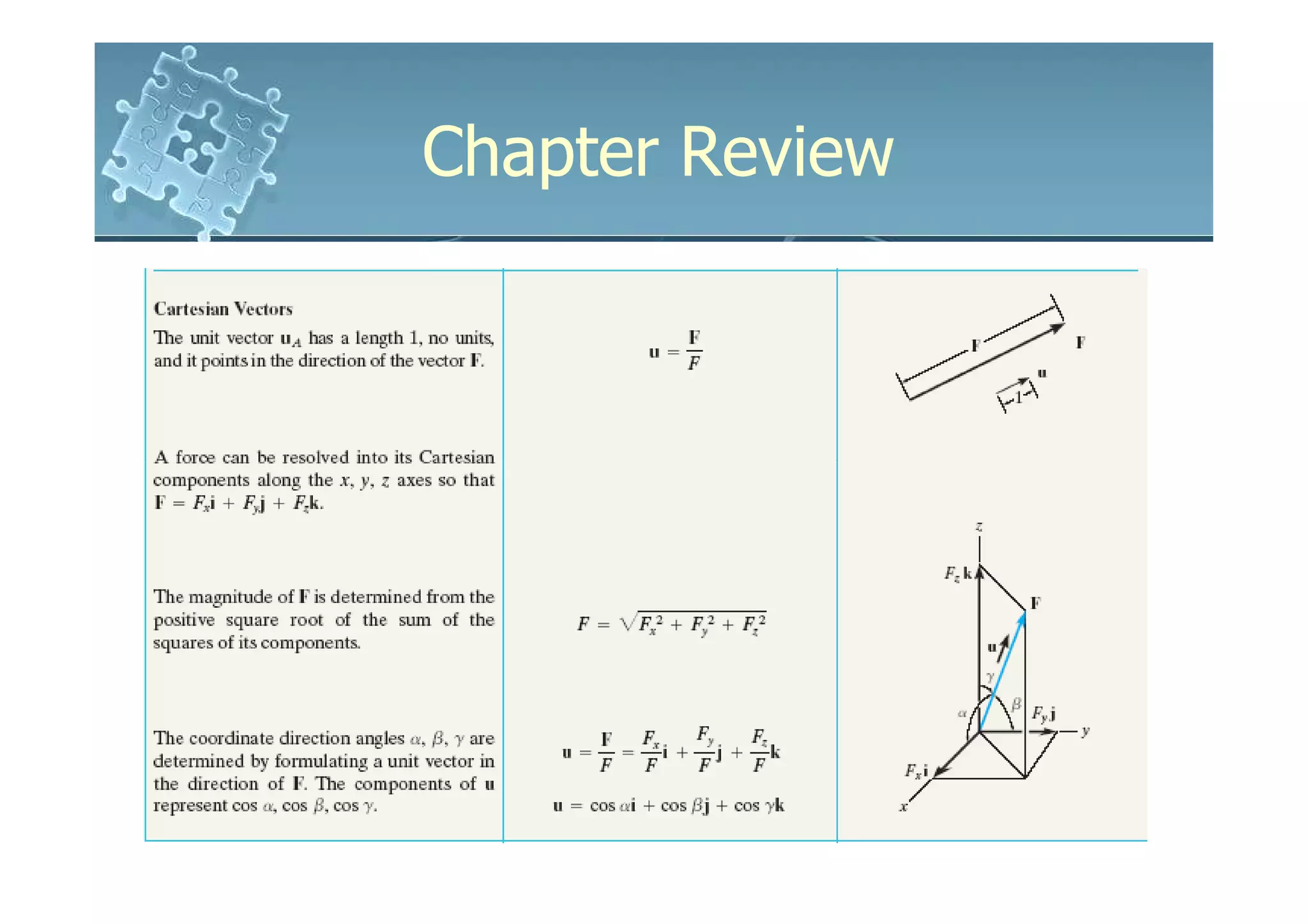
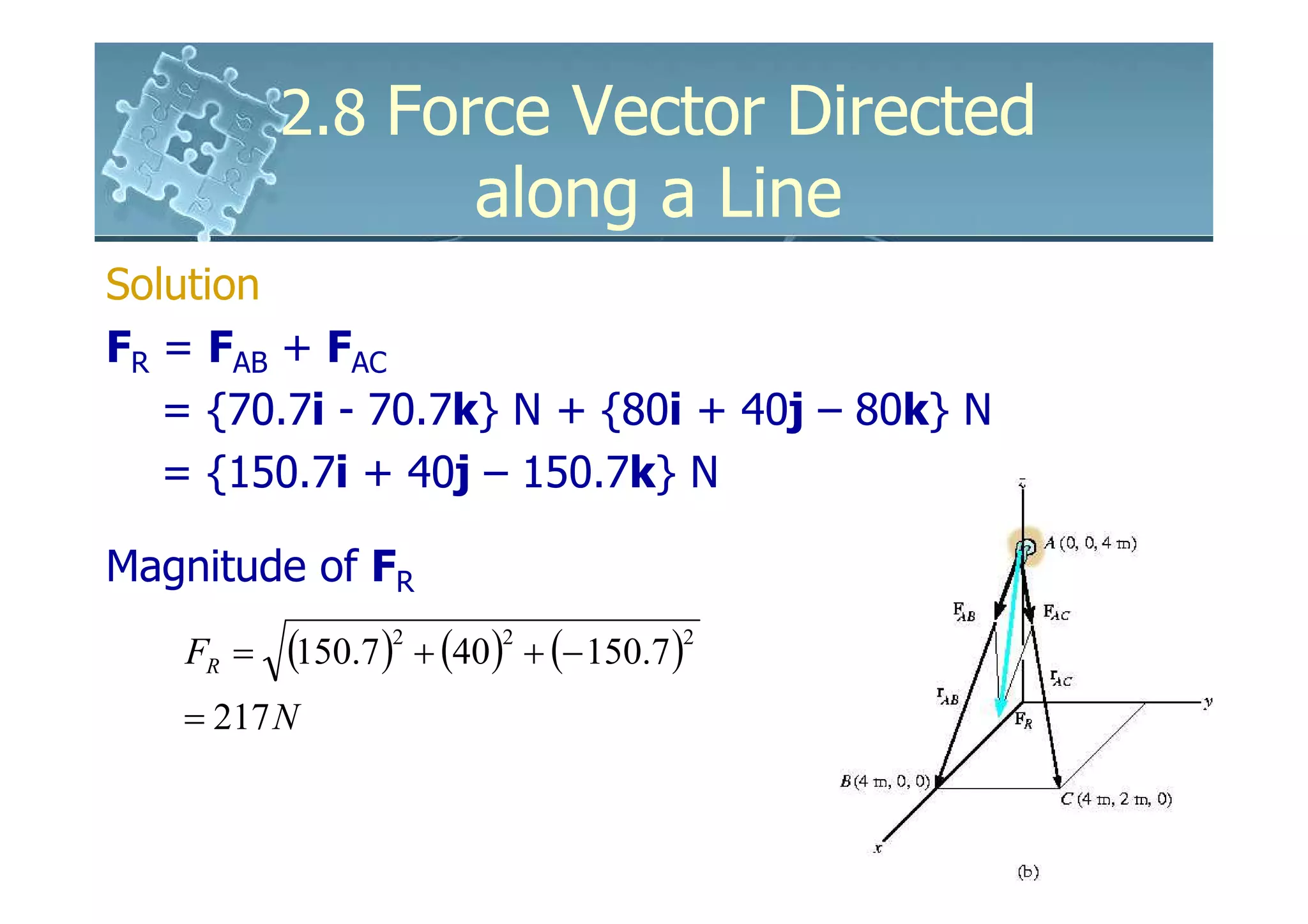
1) Cartesian vectors allow representation of forces and displacements in 3D space using their x, y, z components. 2) Vectors can be added by adding their corresponding x, y, z components. This allows determining resultant forces and displacements. 3) The direction of a vector can be specified by its direction cosines or by defining a unit vector in its direction. 4) Position vectors define the location of a point in space relative to a reference origin. Force vectors can be defined along a line by using the position vector between two points and the force magnitude.

1. 2.6 Addition and Subtraction
of Cartesian Vectors
Example
Given: A = Axi + Ayj + AZk
and B = Bxi + Byj + BZk
Vector Addition
Resultant R = A + B
= (Ax + Bx)i + (Ay + By )j + (AZ + BZ) k
Vector Substraction
Resultant R = A - B
= (Ax - Bx)i + (Ay - By )j + (AZ - BZ) k

2. 2.6 Addition and Subtraction
of Cartesian Vectors
Concurrent Force Systems
- Force resultant is the vector sum of all
the forces in the system
FR = ∑F = ∑Fxi + ∑Fyj + ∑Fzk
where ∑Fx , ∑Fy and ∑Fz represent the
algebraic sums of the x, y and z or i, j or k
components of each force in the system

3. 2.6 Addition and Subtraction
of Cartesian Vectors
Force, F that the tie down rope exerts on the
ground support at O is directed along the rope
Angles α, β and γ can be solved with axes x, y
and z

4. 2.6 Addition and Subtraction
of Cartesian Vectors
Cosines of their values forms a unit vector u that
acts in the direction of the rope
Force F has a magnitude of F
F = Fu = Fcosαi + Fcosβj + Fcosγk

5. 2.6 Addition and Subtraction
of Cartesian Vectors
Example 2.8
Express the force F as Cartesian vector

6. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
Since two angles are specified, the third
angle is found by
cos 2 α + cos 2 β + cos 2 γ = 1
cos 2 α + cos 2 60o + cos 2 45o = 1
cos α = 1 − (0.5) − (0.707 ) = ±0.5
2 2
Two possibilities exit, namely
α = cos −1 (0.5) = 60o or α = cos −1 (− 0.5) = 120o

7. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
By inspection, α = 60° since Fx is in the +x
direction
Given F = 200N
F = Fcosαi + Fcosβj + Fcosγk
= (200cos60°N)i + (200cos60°N)j
+ (200cos45°N)k
= {100.0i + 100.0j + 141.4k}N
Checking: F = Fx2 + Fy2 + Fz2
= (100.0) + (100.0) + (141.4)
2 2 2
= 200 N

8. 2.6 Addition and Subtraction of
Cartesian Vectors
Example 2.9
Determine the magnitude and coordinate
direction angles of resultant force acting on
the ring

9. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
Resultant force
FR = ∑F
= F1 + F2
= {60j + 80k}kN
+ {50i - 100j + 100k}kN
= {50j -40k + 180k}kN
Magnitude of FR is found by
FR = (50)2 + (− 40)2 + (180)2
= 191.0 = 191kN

10. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
Unit vector acting in the direction of FR
uFR = FR /FR
= (50/191.0)i + (40/191.0)j +
(180/191.0)k
= 0.1617i - 0.2094j + 0.9422k
So that
cosα = 0.2617 α = 74.8°
cos β = -0.2094 β = 102°
cosγ = 0.9422 γ = 19.6°
*Note β > 90° since j component of uFR is negative

11. 2.6 Addition and Subtraction
of Cartesian Vectors
Example 2.10
Express the force F1 as a Cartesian vector.

12. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
The angles of 60° and 45° are not coordinate
direction angles.
By two successive applications of
parallelogram law,

13. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
By trigonometry,
F1z = 100sin60 °kN = 86.6kN
F’ = 100cos60 °kN = 50kN
F1x = 50cos45 °kN = 35.4kN
kN
F1y = 50sin45 °kN = 35.4kN
F1y has a direction defined by –j,
Therefore
F1 = {35.4i – 35.4j + 86.6k}kN

14. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
Checking:
F1 = F12 + F12 + F12
x y z
= (35.4)2 + (− 35.4)2 + (86.6)2 = 100 N
Unit vector acting in the direction of F1
u1 = F1 /F1
= (35.4/100)i - (35.4/100)j + (86.6/100)k
= 0.354i - 0.354j + 0.866k

15. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
α1 = cos-1(0.354) = 69.3°
β1 = cos-1(-0.354) = 111°
γ1 = cos-1(0.866) = 30.0°
Using the same method,
F2 = {106i + 184j - 212k}kN

16. 2.6 Addition and Subtraction
of Cartesian Vectors
Example 2.11
Two forces act on the hook. Specify the
coordinate direction angles of F2, so that the
resultant force FR acts along the positive y axis
and has a magnitude of 800N.

17. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
Cartesian vector form
FR = F1 + F2
F1 = F1cosα1i + F1cosβ1j + F1cosγ1k
= (300cos45°N)i + (300cos60°N)j
+ (300cos120°N)k
= {212.1i + 150j - 150k}N
F2 = F2xi + F2yj + F2zk

18. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
Since FR has a magnitude of 800N and acts
in the +j direction
FR = F1 + F2
800j = 212.1i + 150j - 150k + F2xi + F2yj + F2zk
800j = (212.1 + F2x)i + (150 + F2y)j + (- 50 + F2z)k
To satisfy the equation, the corresponding
components on left and right sides must be equal

19. 2.6 Addition and Subtraction
of Cartesian Vectors
Solution
Hence,
0 = 212.1 + F2x F2x = -212.1N
800 = 150 + F2y F2y = 650N
0 = -150 + F2z F2z = 150N
Since magnitude of F2 and its components
are known,
α1 = cos-1(-212.1/700) = 108°
β1 = cos-1(650/700) = 21.8°
γ1 = cos-1(150/700) = 77.6°

20. 2.7 Position Vectors
x,y,z Coordinates
- Right-handed coordinate system
- Positive z axis points upwards, measuring
the height of an object or the altitude of a
point
- Points are measured relative to the
origin, O.

21. 2.7 Position Vectors
x,y,z Coordinates
Eg: For Point A, xA = +4m along the x axis,
yA = -6m along the y axis and zA = -6m
along the z axis. Thus, A (4, 2, -6)
Similarly, B (0, 2, 0) and C (6, -1, 4)

22. 2.7 Position Vectors
Position Vector
- Position vector r is defined as a fixed vector
which locates a point in space relative to another
point.
Eg: If r extends from the
origin, O to point P (x, y, z)
then, in Cartesian vector
form
r = xi + yj + zk

23. 2.7 Position Vectors
Position Vector
Note the head to tail vector addition of the
three components
Start at origin O, one travels x in the +i direction,
y in the +j direction and z in the +k direction,
arriving at point P (x, y, z)

24. 2.7 Position Vectors
Position Vector
- Position vector maybe directed from point A to
point B
- Designated by r or rAB
Vector addition gives
rA + r = rB
Solving
r = rB – rA = (xB – xA)i + (yB – yA)j + (zB –zA)k
or r = (xB – xA)i + (yB – yA)j + (zB –zA)k

25. 2.7 Position Vectors
Position Vector
- The i, j, k components of the positive vector r
may be formed by taking the coordinates of the
tail, A (xA, yA, zA) and subtract them from the
head B (xB, yB, zB)
Note the head to tail vector addition of the
three components

26. 2.7 Position Vectors
Length and direction of
cable AB can be found by
measuring A and B using
the x, y, z axes
Position vector r can be
established
Magnitude r represent
the length of cable

27. 2.7 Position Vectors
Angles, α, β and γ
represent the direction
of the cable
Unit vector, u = r/r

28. 2.7 Position Vectors
Example 2.12
An elastic rubber band is
attached to points A and B.
Determine its length and
its
direction measured from A
towards B.

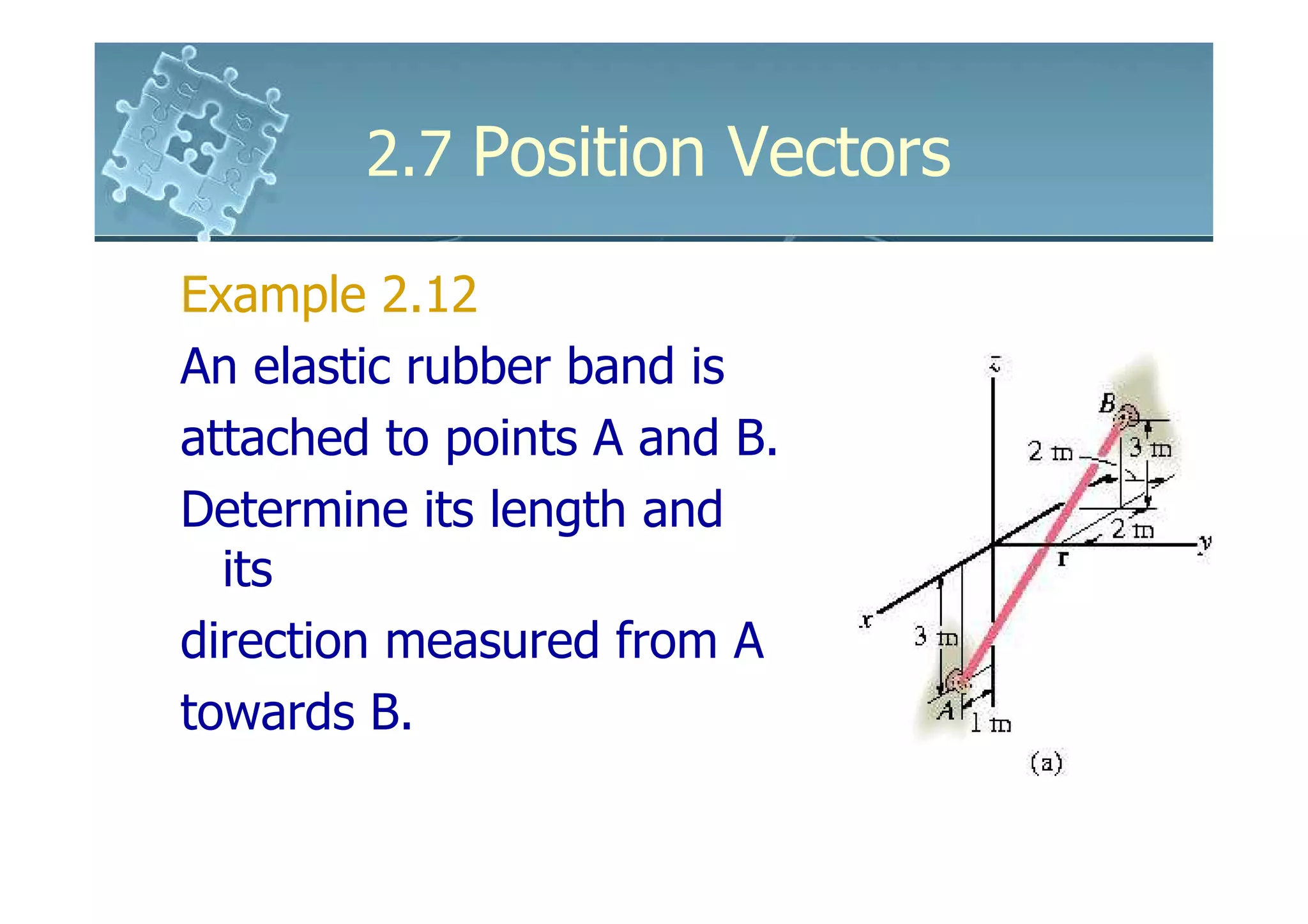
29. 2.7 Position Vectors
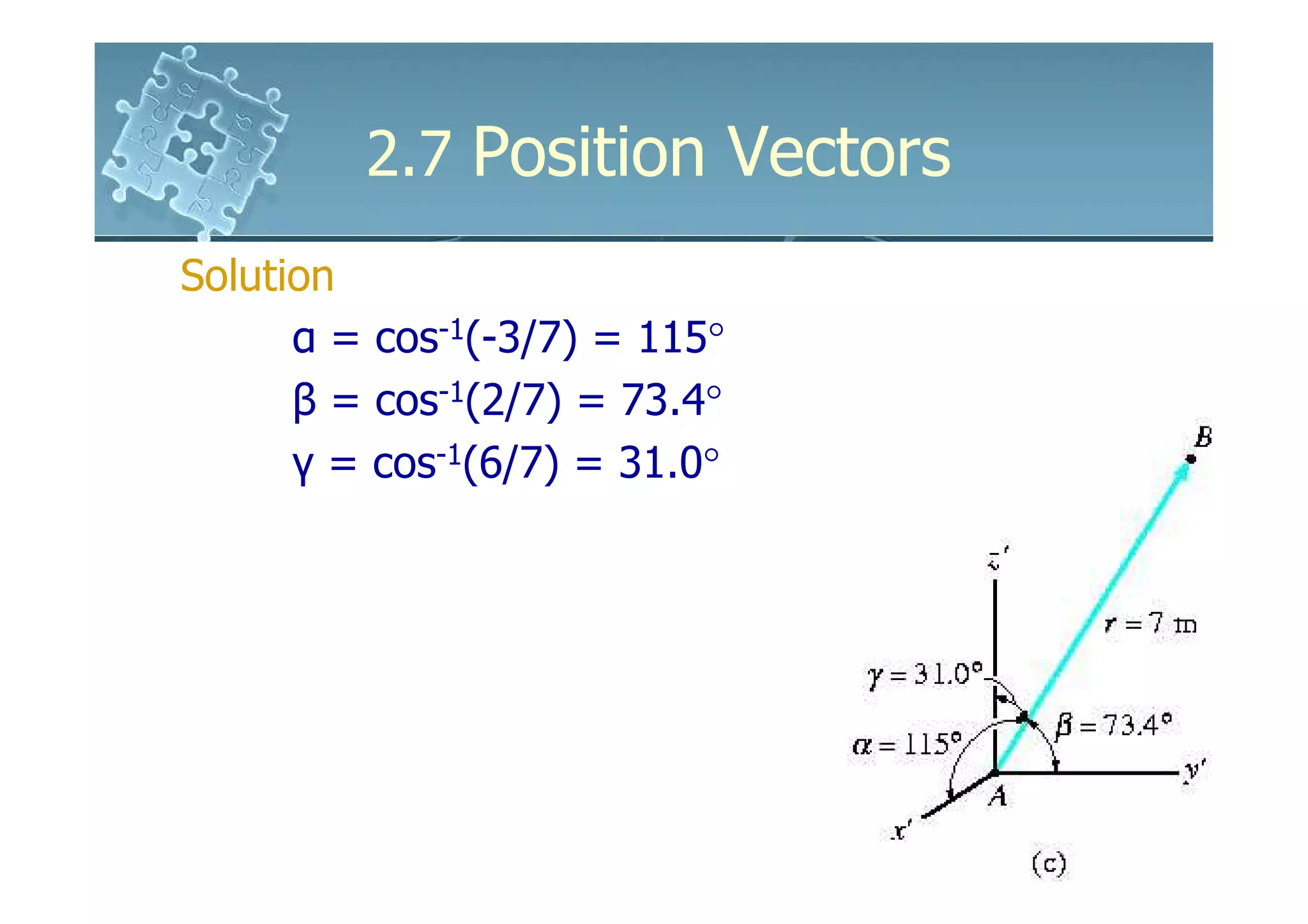
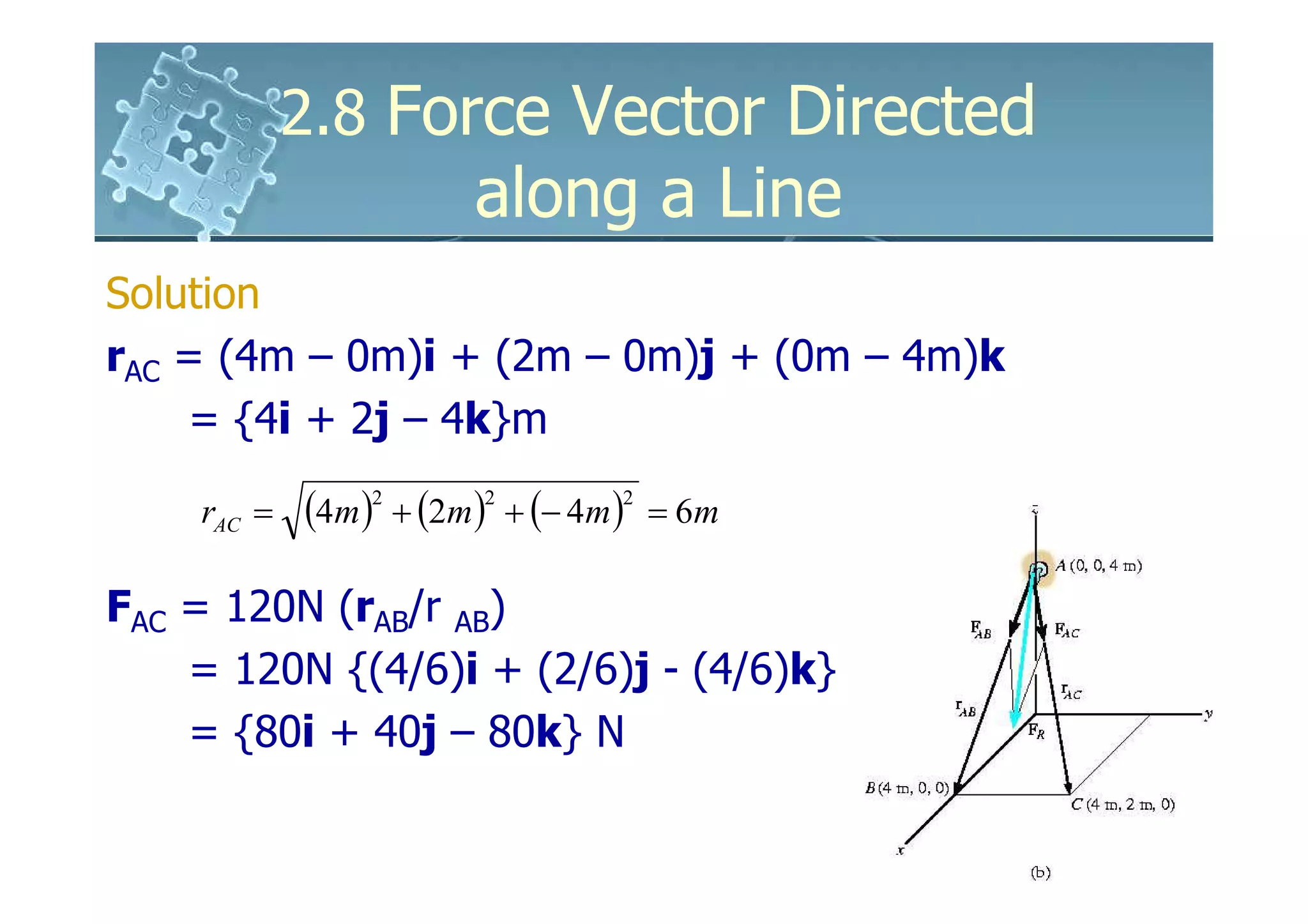
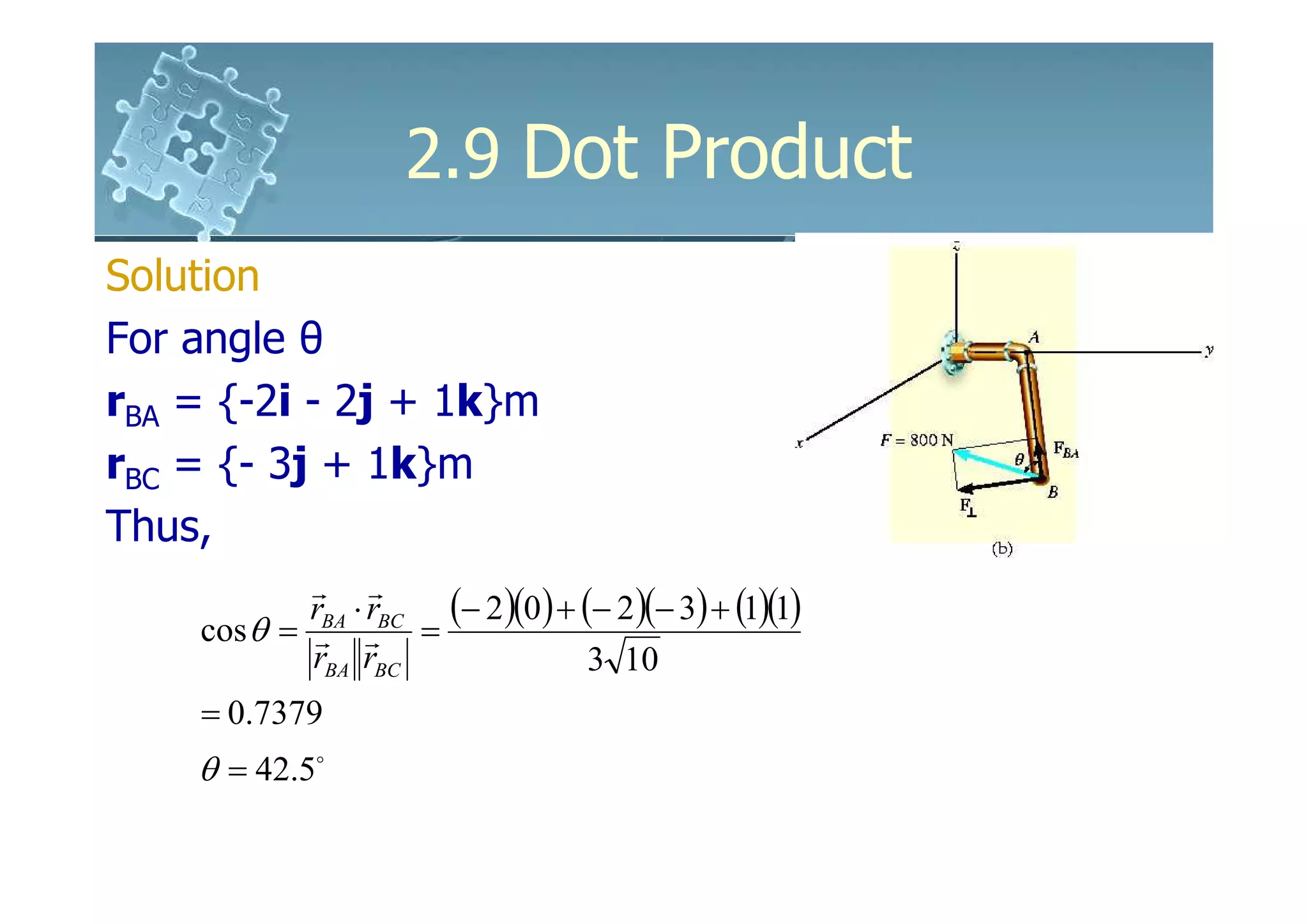
Solution
Position vector
r = [-2m – 1m]i + [2m – 0]j + [3m – (-3m)]k
= {-3i + 2j + 6k}m
Magnitude = length of the rubber band
r= (− 3)2 + (2)2 + (6)2 = 7m
Unit vector in the director of r
u = r /r
= -3/7i + 2/7j + 6/7k

30. 2.7 Position Vectors
Solution
α = cos-1(-3/7) = 115°
β = cos-1(2/7) = 73.4°
γ = cos-1(6/7) = 31.0°

31. 2.8 Force Vector Directed
along a Line
In 3D problems, direction of F is specified by
2 points, through which its line of action lies
F can be formulated as a Cartesian vector
F = F u = F (r/r)
Note that F has units of
forces (N) unlike r, with
units of length (m)

32. 2.8 Force Vector Directed
along a Line
Force F acting along the chain can be
presented as a Cartesian vector by
- Establish x, y, z axes
- Form a position vector r along length of
chain

33. 2.8 Force Vector Directed
along a Line
Unit vector, u = r/r that defines the direction
of both the chain and the force
We get F = Fu

34. 2.8 Force Vector Directed
along a Line
Example 2.13
The man pulls on the cord
with a force of 350N.
Represent this force acting
on the support A, as a
Cartesian vector and
determine its direction.

35. 2.8 Force Vector Directed
along a Line
Solution
End points of the cord are A (0m, 0m, 7.5m)
and B (3m, -2m, 1.5m)
r = (3m – 0m)i + (-2m – 0m)j + (1.5m –
7.5m)k
= {3i – 2j – 6k}m
Magnitude = length of cord AB
r = (3m ) + (− 2m ) + (− 6m ) = 7m
2 2 2
Unit vector, u = r /r
= 3/7i - 2/7j - 6/7k

36. 2.8 Force Vector Directed
along a Line
Solution
Force F has a magnitude of 350N, direction
specified by u
F = Fu
= 350N(3/7i - 2/7j - 6/7k)
= {150i - 100j - 300k} N
α = cos-1(3/7) = 64.6°
β = cos-1(-2/7) = 107°
γ = cos-1(-6/7) = 149°

37. 2.8 Force Vector Directed
along a Line
Example 2.14
The circular plate is
partially supported by
the cable AB. If the
force of the cable on
the
hook at A is F = 500N,
express F as a
Cartesian vector.

38. 2.8 Force Vector Directed
along a Line
Solution
End points of the cable are (0m, 0m, 2m) and B
(1.707m, 0.707m, 0m)
r = (1.707m – 0m)i + (0.707m – 0m)j
+ (0m – 2m)k
= {1.707i + 0.707j - 2k}m
Magnitude = length of cable AB
r= (1.707m )2 + (0.707m )2 + (− 2m )2 = 2.723m

39. 2.8 Force Vector Directed
along a Line
Solution
Unit vector,
u = r /r
= (1.707/2.723)i + (0.707/2.723)j – (2/2.723)k
= 0.6269i + 0.2597j – 0.7345k
For force F,
F = Fu
= 500N(0.6269i + 0.2597j – 0.7345k)
= {313i - 130j - 367k} N

40. 2.8 Force Vector Directed
along a Line
Solution
Checking
F= (313) + (130) + (− 367 )
2 2 2
= 500 N
Show that γ = 137° and
indicate this angle on the
diagram

41. 2.8 Force Vector Directed
along a Line
Example 2.15
The roof is supported by
cables. If the cables exert
FAB = 100N and FAC = 120N
on the wall hook at A,
determine the magnitude of
the resultant force acting at
A.

42. 2.8 Force Vector Directed
along a Line
Solution
rAB = (4m – 0m)i + (0m – 0m)j + (0m – 4m)k
= {4i – 4k}m
rAB = (4m )2 + (− 4m )2 = 5.66m
FAB = 100N (rAB/r AB)
= 100N {(4/5.66)i - (4/5.66)k}
= {70.7i - 70.7k} N

43. 2.8 Force Vector Directed
along a Line
Solution
rAC = (4m – 0m)i + (2m – 0m)j + (0m – 4m)k
= {4i + 2j – 4k}m
rAC = (4m )2 + (2m )2 + (− 4m )2 = 6m
FAC = 120N (rAB/r AB)
= 120N {(4/6)i + (2/6)j - (4/6)k}
= {80i + 40j – 80k} N

44. 2.8 Force Vector Directed
along a Line
Solution
FR = FAB + FAC
= {70.7i - 70.7k} N + {80i + 40j – 80k} N
= {150.7i + 40j – 150.7k} N
Magnitude of FR
FR = (150.7 )2 + (40)2 + (− 150.7 )2
= 217 N

45. 2.9 Dot Product
Dot product of vectors A and B is written
as A·B (Read A dot B)
Define the magnitudes of A and B and the
angle between their tails
A·B = AB cosθ where 0°≤ θ ≤180°
Referred to as scalar
product of vectors as
result is a scalar

46. 2.9 Dot Product
Laws of Operation
1. Commutative law
A·B = B·A
2. Multiplication by a scalar
a(A·B) = (aA)·B = A·(aB) = (A·B)a
3. Distribution law
A·(B + D) = (A·B) + (A·D)

47. 2.9 Dot Product
Cartesian Vector Formulation
- Dot product of Cartesian unit vectors
Eg: i·i = (1)(1)cos0° = 1 and
i·j = (1)(1)cos90° = 0
- Similarly
i·i = 1 j·j = 1 k·k = 1
i·j = 0 i·k = 1 j·k = 1

48. 2.9 Dot Product
Cartesian Vector Formulation
- Dot product of 2 vectors A and B
A·B = (Axi + Ayj + Azk)· (Bxi + Byj + Bzk)
= AxBx(i·i) + AxBy(i·j) + AxBz(i·k)
+ AyBx(j·i) + AyBy(j·j) + AyBz(j·k)
+ AzBx(k·i) + AzBy(k·j) + AzBz(k·k)
= AxBx + AyBy + AzBz
Note: since result is a scalar, be careful of including
any unit vectors in the result

49. 2.9 Dot Product
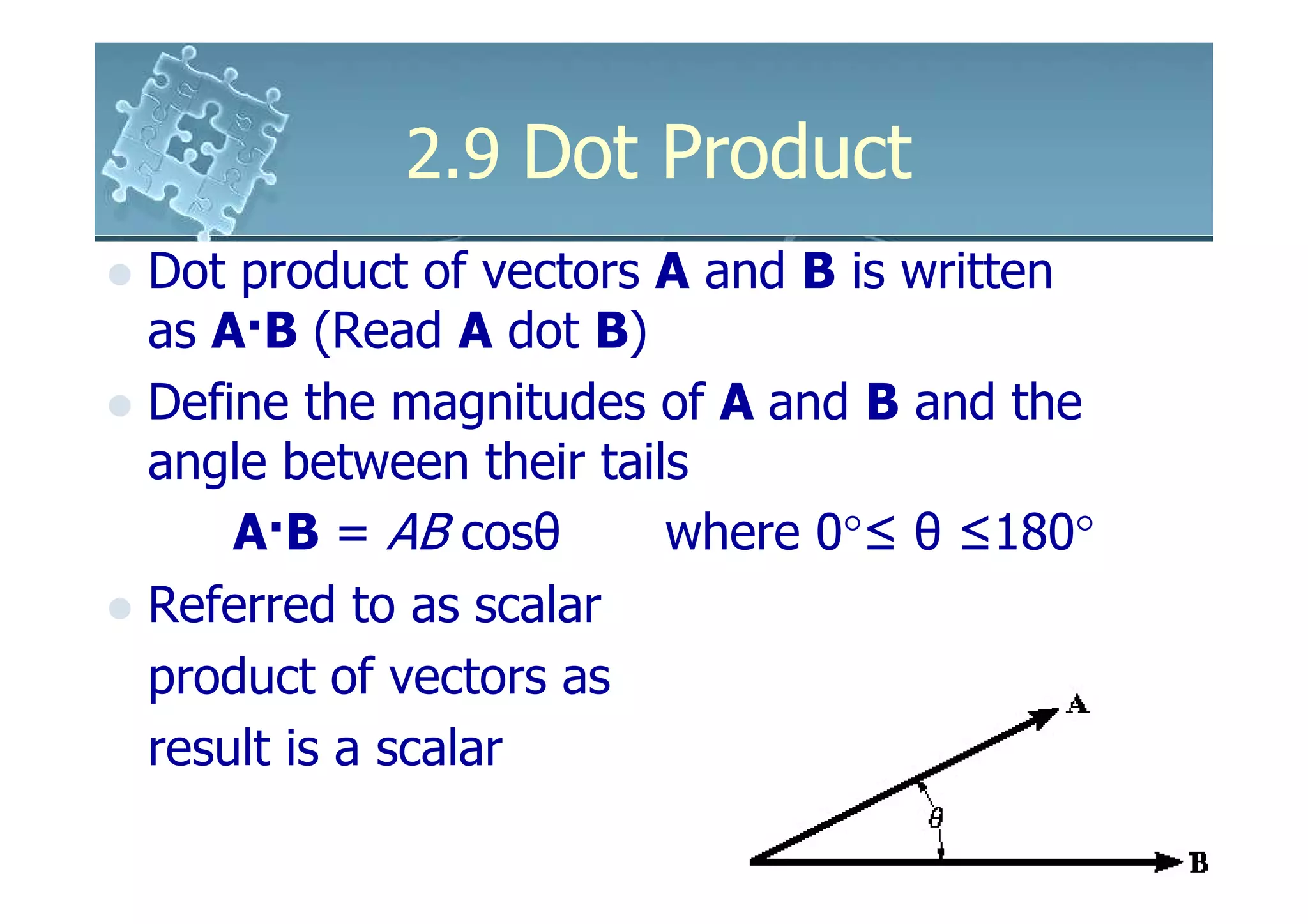
Applications
- The angle formed between two vectors or
intersecting lines
θ = cos-1 [(A·B)/(AB)] 0°≤ θ ≤180°
Note: if A·B = 0, cos-10= 90°, A is
perpendicular to B

50. 2.9 Dot Product
Applications
- The components of a vector parallel and
perpendicular to a line
- Component of A parallel or collinear with line aa’ is
defined by A║ (projection of A onto the line)
A║ = A cos θ
- If direction of line is specified by unit vector u (u =
1),
A║ = A cos θ = A·u

51. 2.9 Dot Product
Applications
- If A║ is positive, A║ has a directional
sense same as u
- If A║ is negative, A║ has a directional
sense opposite to u
- A║ expressed as a vector
A║ = A cos θ u
= (A·u)u

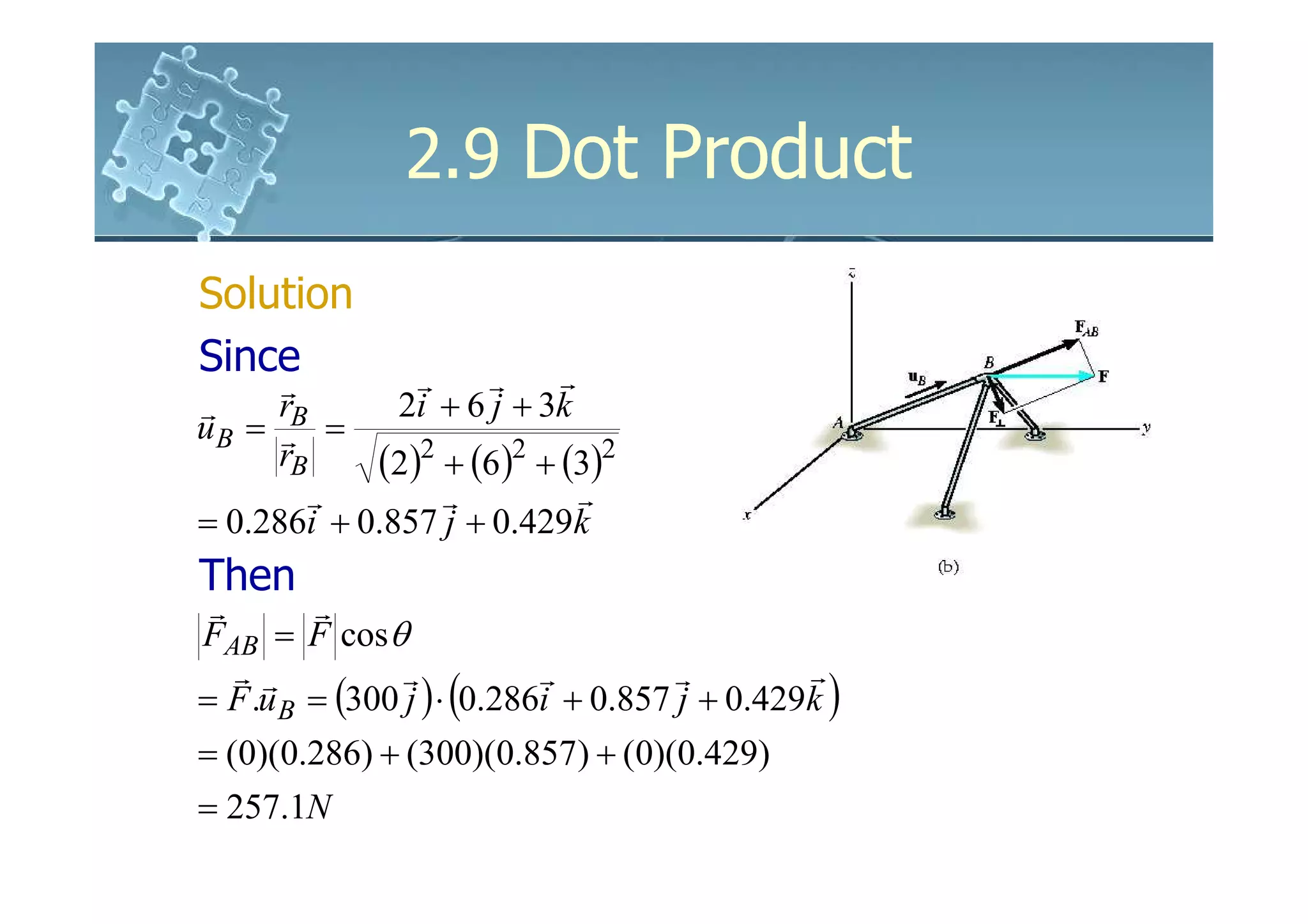
52. 2.9 Dot Product
Applications
For component of A perpendicular to line aa’
1. Since A = A║ + A┴,
then A┴ = A - A║
2. θ = cos-1 [(A·u)/(A)]
then A┴ = Asinθ
3. If A║ is known, by Pythagorean Theorem
A⊥ = A2 + A||2

53. 2.9 Dot Product
For angle θ between the
rope and the beam A,
- Unit vectors along the
beams, uA = rA/rA
- Unit vectors along the
ropes, ur=rr/rr
- Angle θ = cos-1
(rA.rr/rArr)
= cos-1 (uA· ur)

54. 2.9 Dot Product
For projection of the force
along the beam A
- Define direction of the beam
uA = rA/rA
- Force as a Cartesian vector
F = F(rr/rr) = Fur
- Dot product
F║ = F║·uA

55. 2.9 Dot Product
Example 2.16
The frame is subjected to a horizontal force
F = {300j} N. Determine the components of
this force parallel and perpendicular to the
member AB.

56. 2.9 Dot Product
Solution
Since r r r
r
r r 2i + 6 j + 3k
u B = rB =
rB (2)2 + (6)2 + (3)2
r r r
= 0.286i + 0.857 j + 0.429k
Then
r r
FAB = F cosθ
rr r r r r
= F .u B = (300 j ) ⋅ (0.286i + 0.857 j + 0.429k )
= (0)(0.286) + (300)(0.857) + (0)(0.429)
= 257.1N

57. 2.9 Dot Product
Solution
Since result is a positive scalar,
FAB has the same sense of
direction as uB. Express in
Cartesian form
r r r
FAB = FAB u AB
r r r
= (257.1N )(0.286i + 0.857 j + 0.429k )
r r r
= {73.5i + 220 j + 110k }N
Perpendicular component
r r r r r r r r r r
F⊥ = F − FAB = 300 j − (73.5i + 220 j + 110k ) = {−73.5i + 80 j − 110k }N

58. 2.9 Dot Product
Solution
Magnitude can be determined
From F┴ or from Pythagorean
Theorem
r r2 r 2
F⊥ = F − FAB
= (300 N )2 − (257.1N )2
= 155 N

59. 2.9 Dot Product
Example 2.17
The pipe is subjected to F = 800N. Determine the
angle θ between F and pipe segment BA, and the
magnitudes of the components of F, which are
parallel and perpendicular to BA.

60. 2.9 Dot Product
Solution
For angle θ
rBA = {-2i - 2j + 1k}m
rBC = {- 3j + 1k}m
Thus,
r r
rBA ⋅ rBC (− 2 )(0 ) + (− 2 )(− 3) + (1)(1)
cos θ = r r =
rBA rBC 3 10
= 0.7379
θ = 42.5o

61. 2.9 Dot Product
Solution
Components ofr F
r r r
r r (−2i − 2 j + 1k )
u AB = rAB =
rAB 3
r
 − 2 i +  − 2  r +  1  k
r
=   j  
 3   3   3
r rr
FAB = F .u B
r r  2 r  2  r  1  r
= (− 758.9 j + 253.0k ) ⋅  − i +  −  j +  k
 3   3   3
= 0 + 506.0 + 84.3
= 590 N

62. 2.9 Dot Product
Solution
Checking from trigonometry,
r r
FAB = F cos θ
= 800 cos 42.5o N
= 540 N
Magnitude can be determined
From F┴
r r
F⊥ = F sin θ = 800 sin 42.5o = 540 N

63. 2.9 Dot Product
Solution
Magnitude can be determined from F┴ or from
Pythagorean Theorem
r r2 r 2
F⊥ = F − FAB
= (800)2 − (590)2
= 540 N

64. Chapter Summary
Parallelogram Law
Addition of two vectors
Components form the side and resultant
form the diagonal of the parallelogram
To obtain resultant, use tip to tail addition
by triangle rule
To obtain magnitudes and directions, use
Law of Cosines and Law of Sines

65. Chapter Summary
Cartesian Vectors
Vector F resolved into Cartesian vector form
F = Fxi + Fyj + Fzk
Magnitude of F
2 2 2
F = Fx + Fy + Fz
Coordinate direction angles α, β and γ are
determined by the formulation of the unit
vector in the direction of F
u = (Fx/F)i + (Fy/F)j + (Fz/F)k

66. Chapter Summary
Cartesian Vectors
Components of u represent cosα, cosβ and cosγ
These angles are related by
cos2α + cos2β + cos2γ = 1
Force and Position Vectors
Position Vector is directed between 2 points
Formulated by distance and direction moved
along the x, y and z axes from tail to tip

67. Chapter Summary
Force and Position Vectors
For line of action through the two points, it
acts in the same direction of u as the
position vector
Force expressed as a Cartesian vector
F = Fu = F(r/r)
Dot Product
Dot product between two vectors A and B
A·B = AB cosθ

68. Chapter Summary
Dot Product
Dot product between two vectors A and B
(vectors expressed as Cartesian form)
A·B = AxBx + AyBy + AzBz
For angle between the tails of two vectors
θ = cos-1 [(A·B)/(AB)]
For projected component of A onto an axis
defined by its unit vector u
A = A cos θ = A·u

69. Chapter Review

70. Chapter Review

71. Chapter Review

72. Chapter Review

73. Chapter Review

74. Chapter Review