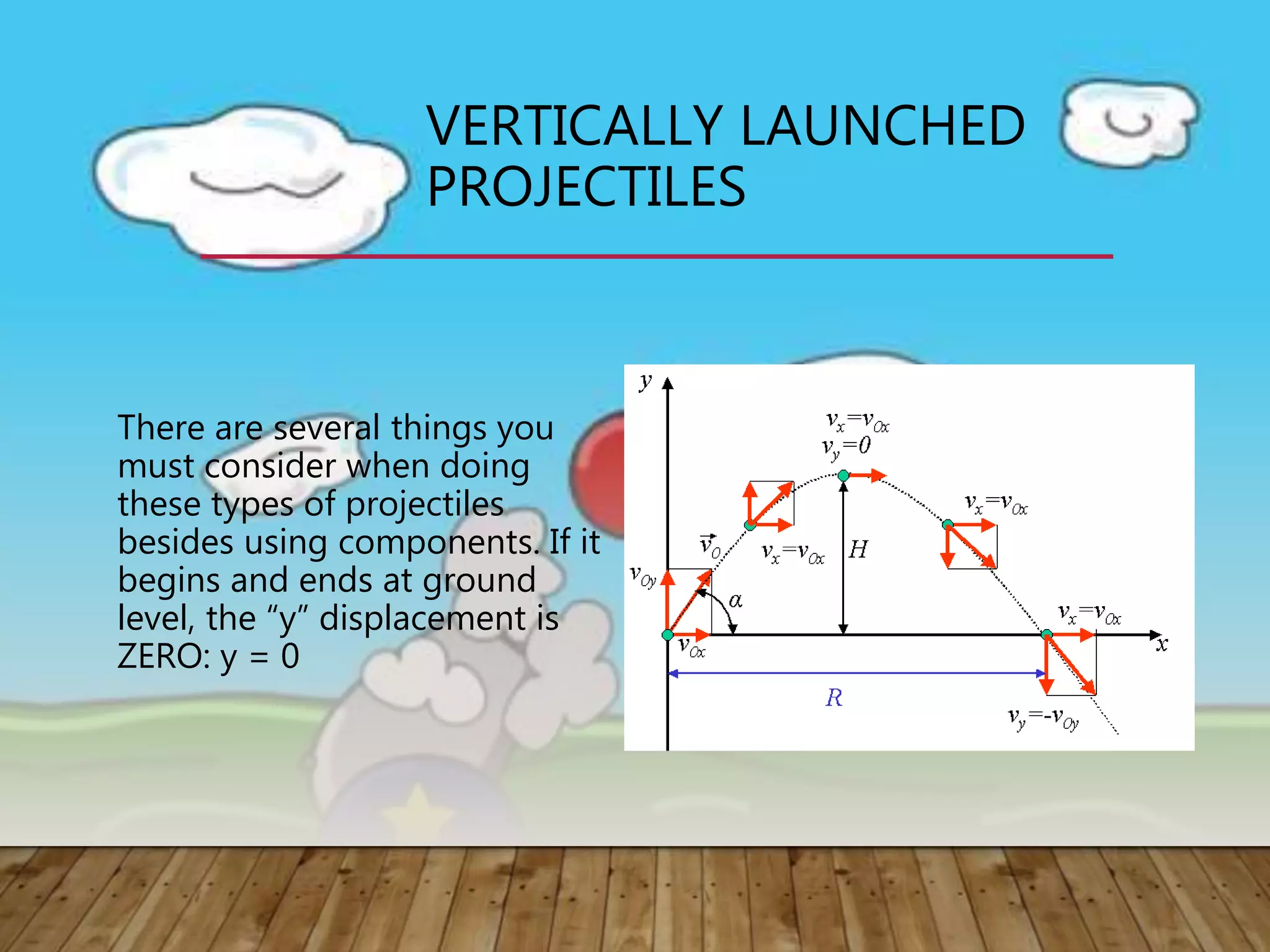
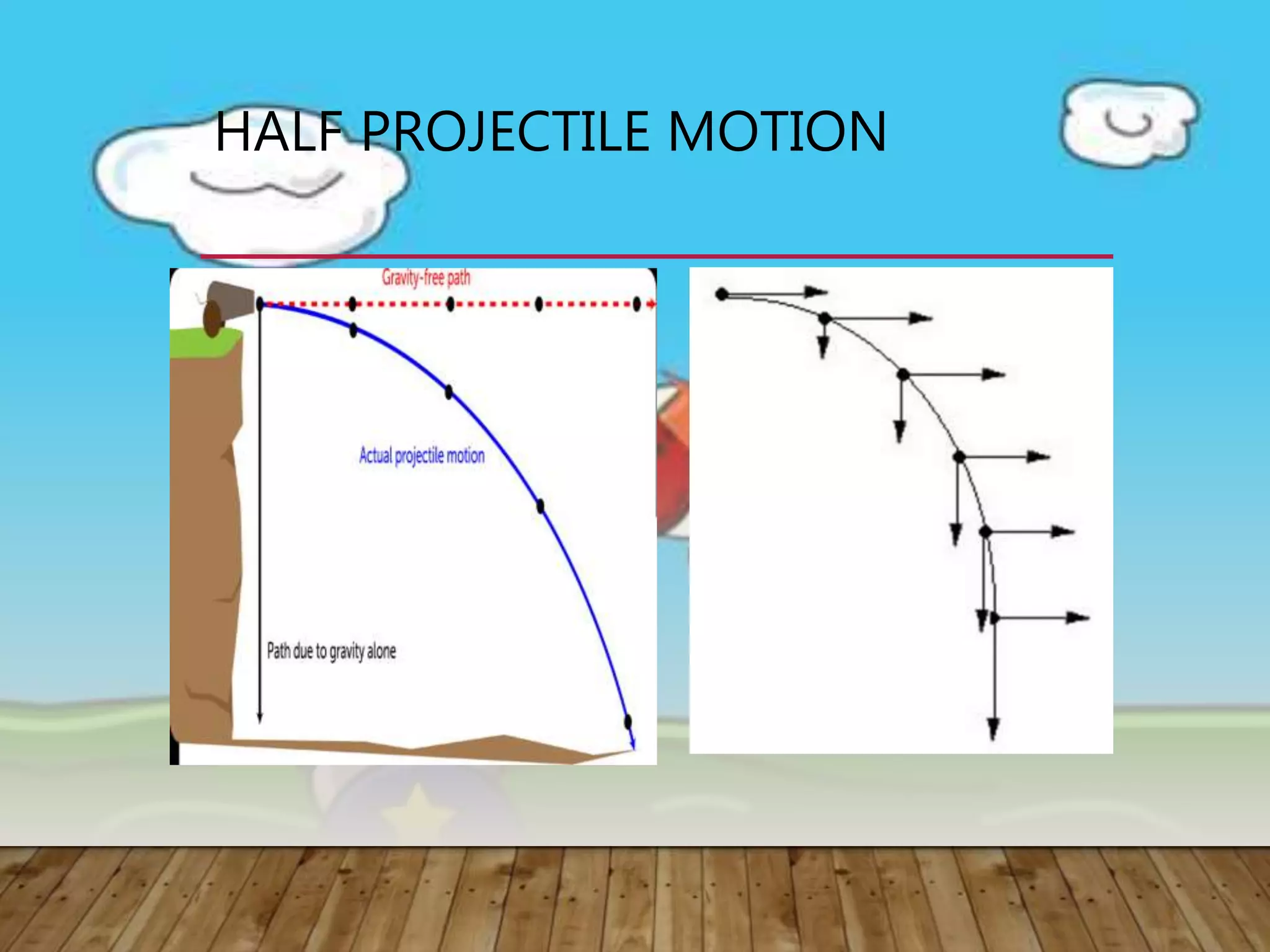
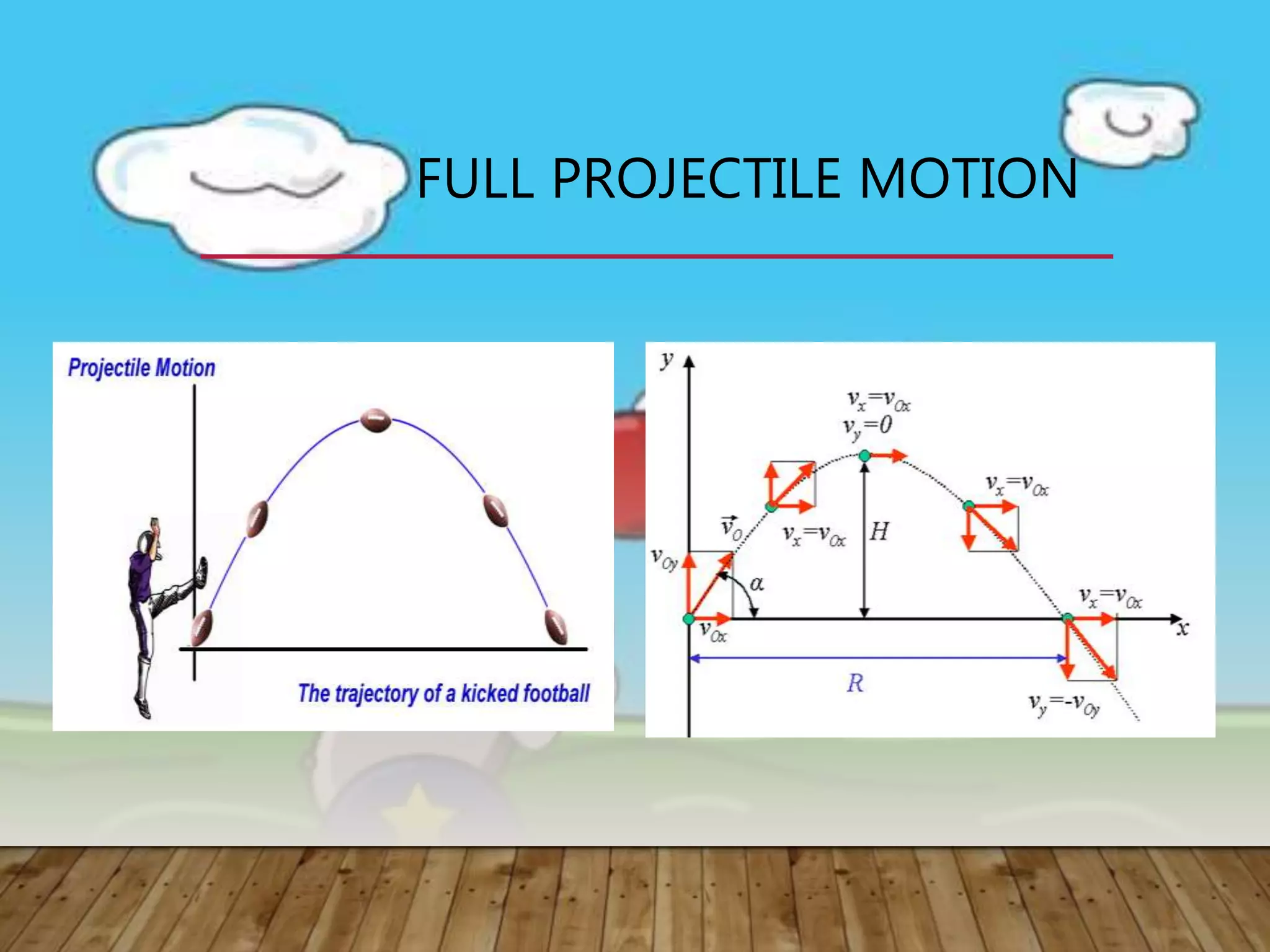
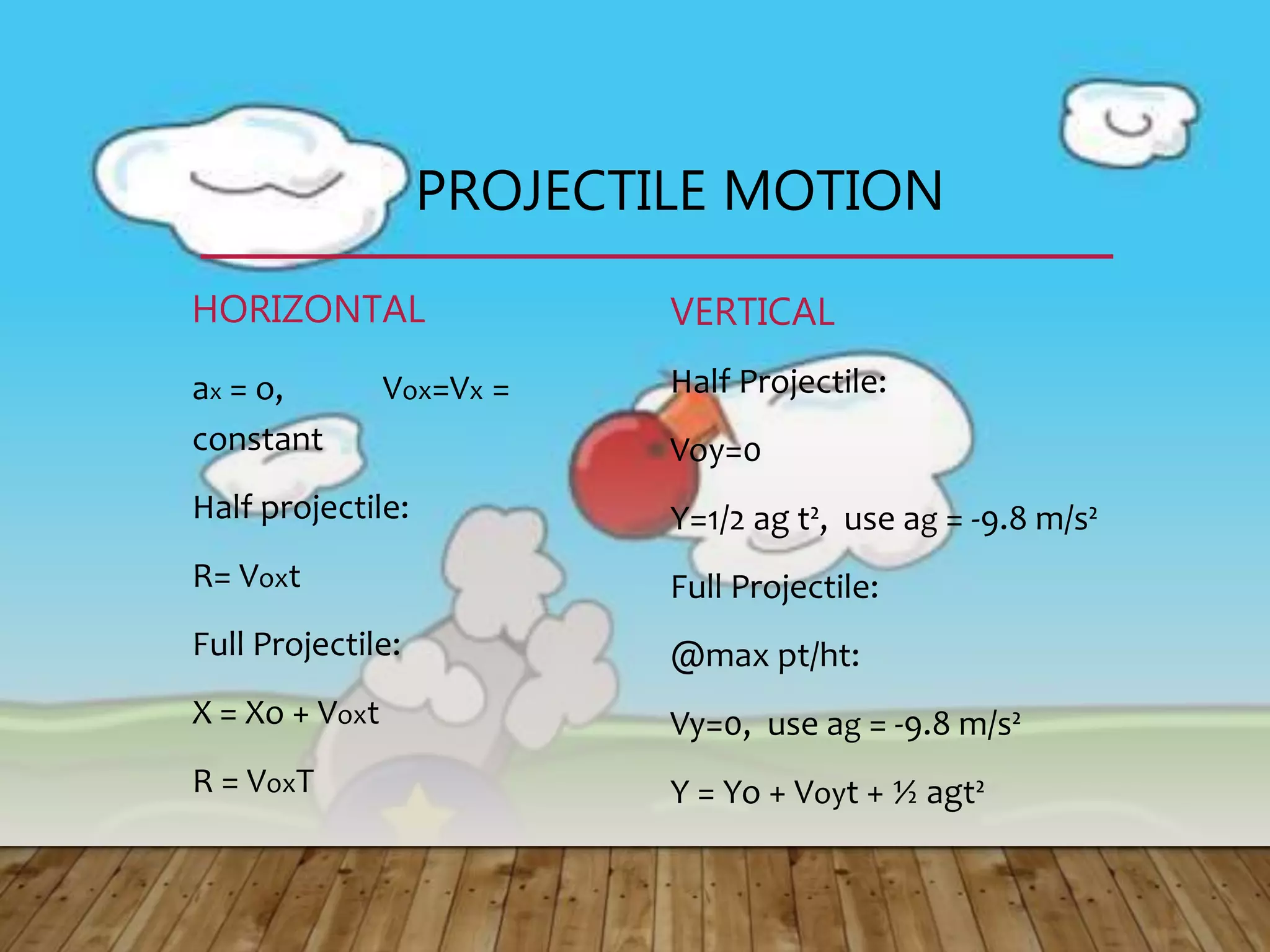
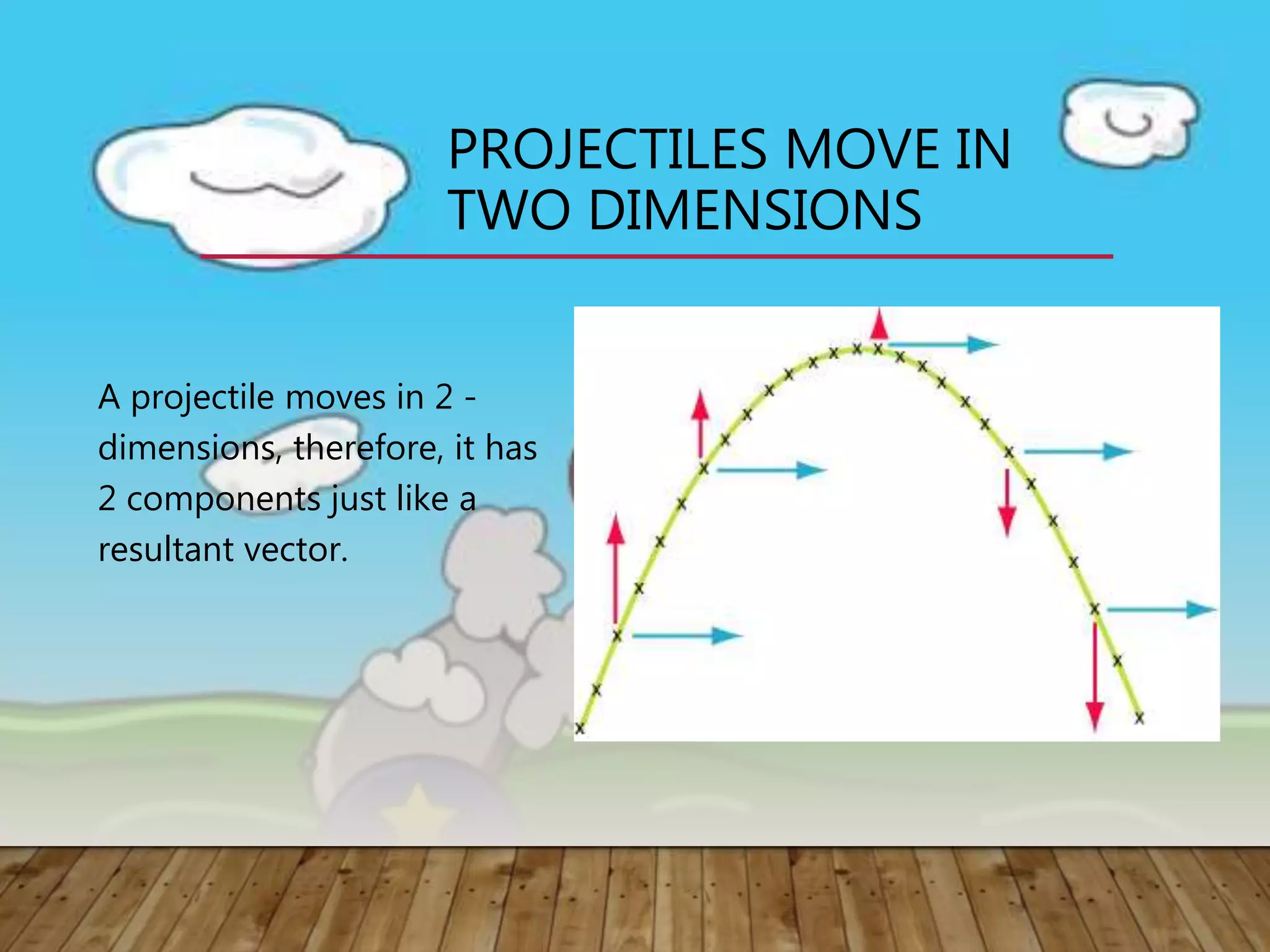
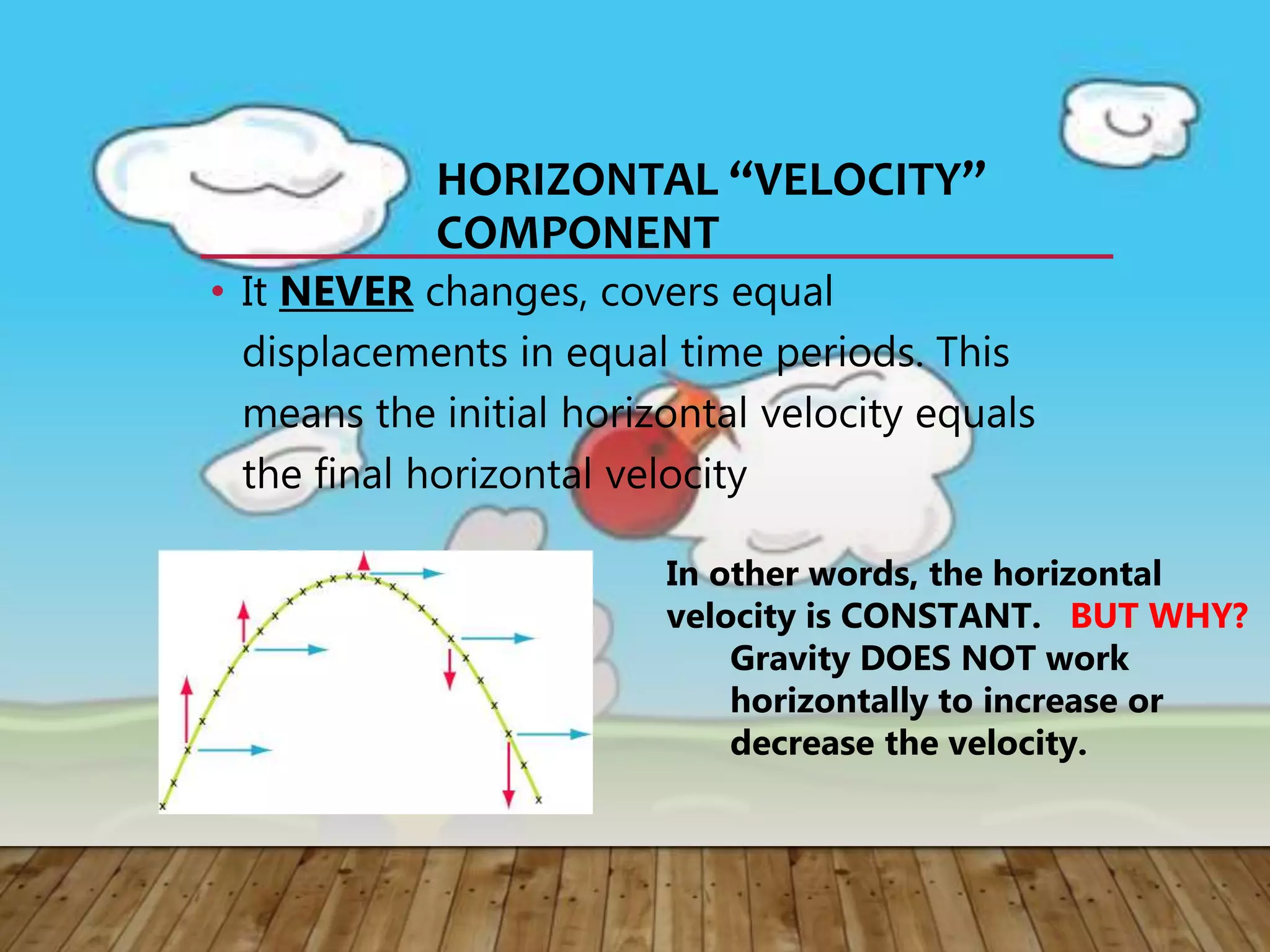
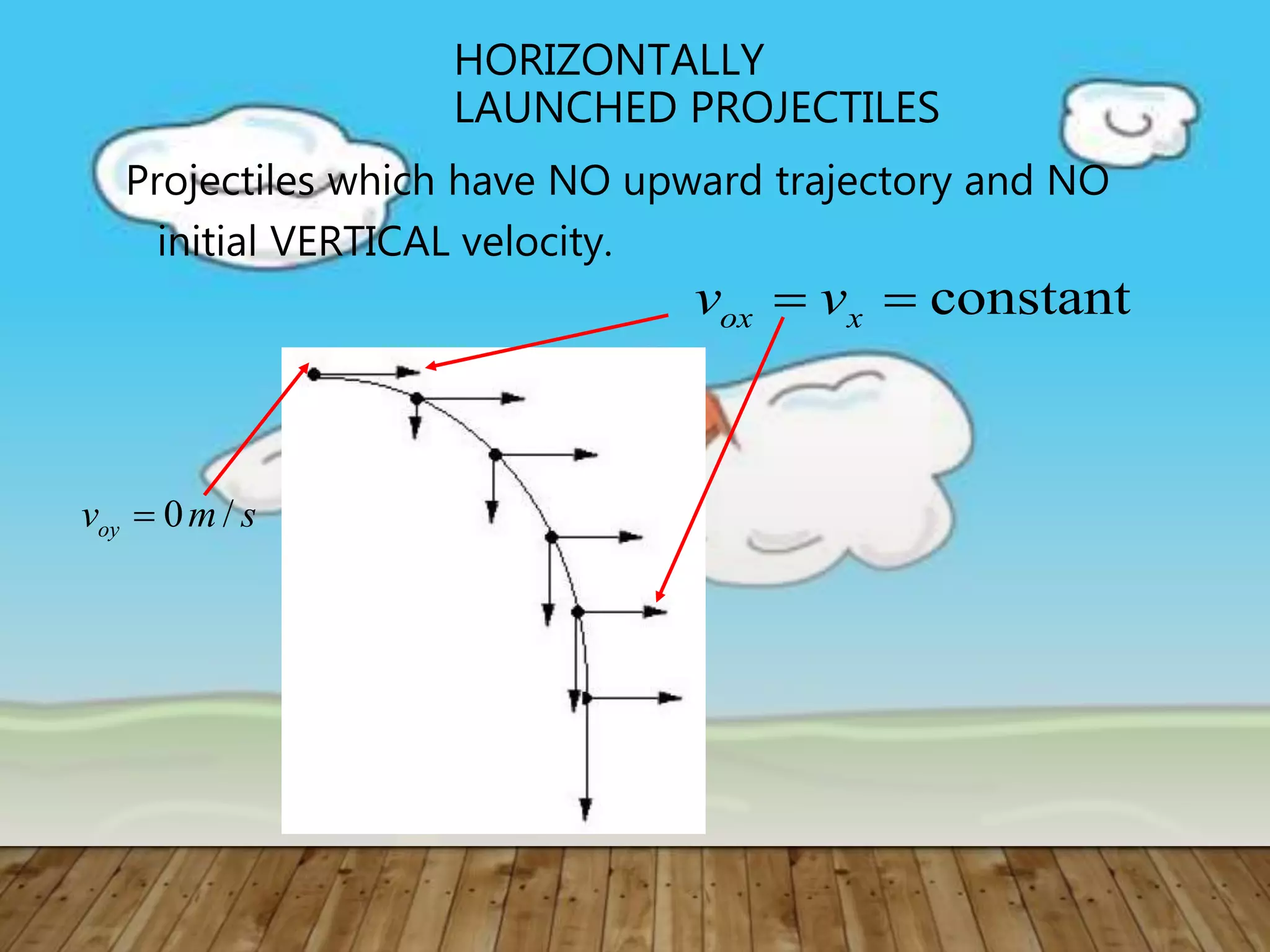
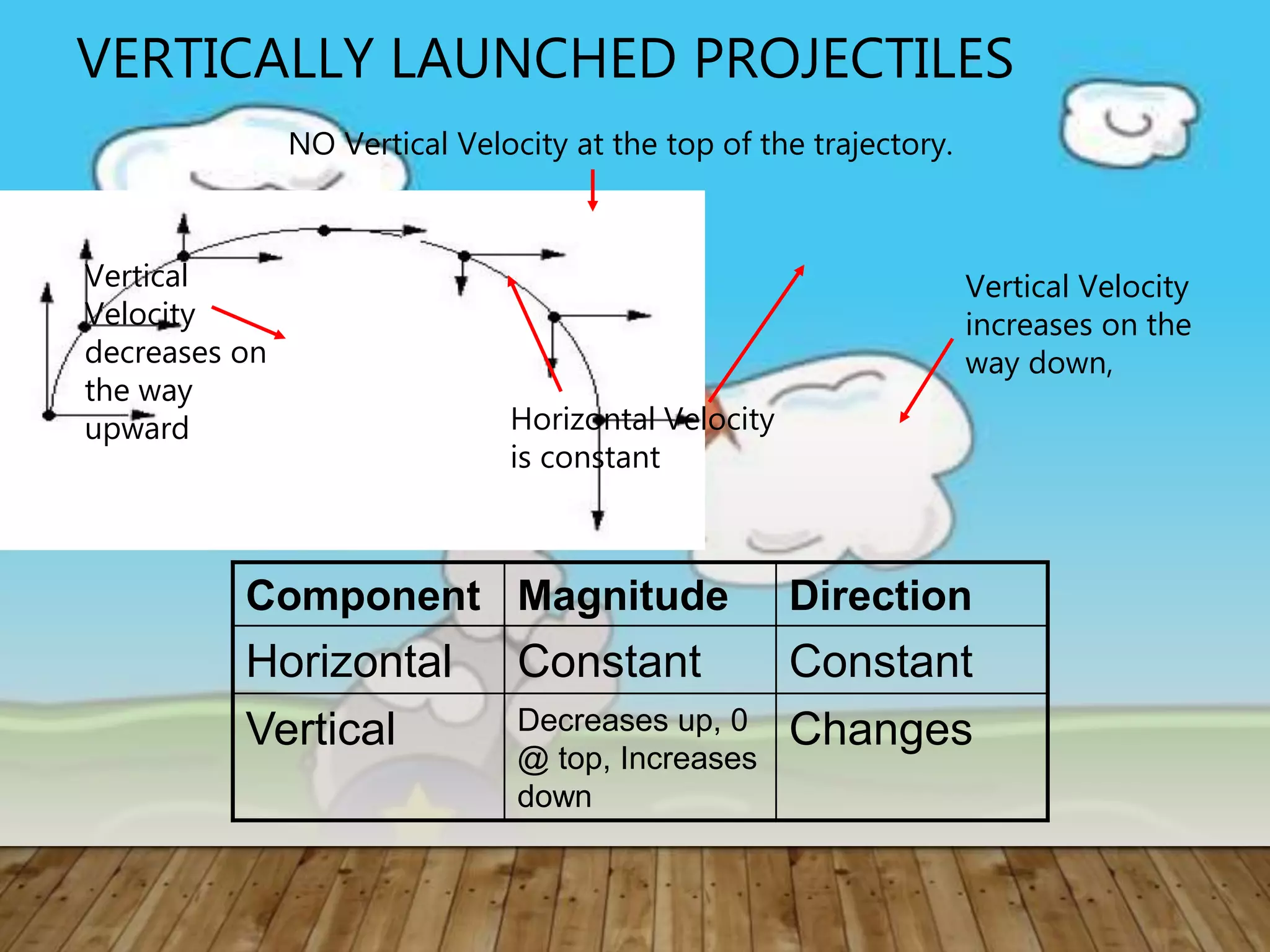
1) Projectile motion describes the trajectory of objects thrown or projected into the air. It is the motion of projectiles that are subject only to gravity. 2) Projectiles have two velocity components - a horizontal component that remains constant, and a vertical component that changes due to gravity. This results in a parabolic trajectory. 3) There are two types of projectile motion - horizontally launched, where the initial vertical velocity is zero, and vertically launched, where the velocity has horizontal and vertical components.

1. PROJECTILE MOTION
by: JANET BRIGIDA A. CATIPON
MHS Science 9 Teacher

2. LEARNING OBJECTIVES
• Define Projectile Motion
• Explain Projectile Motion
• Identify the types of Projectile Motion
• Differentiate the types of Projectile Motion
• Explain and summarize all the kinematics equation
in solving Projectile Motion problems
• Solve problems involving the types of Projectile
Motion

3. WHAT IS PROJECTILE?
Projectile -Any object which projected by some means and continues
to move due to its own inertia (mass).

4. PROJECTILES MOVE IN
TWO DIMENSIONS
A projectile moves in 2 -
dimensions, therefore, it has
2 components just like a
resultant vector.

5. HORIZONTAL “VELOCITY”
COMPONENT
• It NEVER changes, covers equal
displacements in equal time periods. This
means the initial horizontal velocity equals
the final horizontal velocity
In other words, the horizontal
velocity is CONSTANT. BUT WHY?
Gravity DOES NOT work
horizontally to increase or
decrease the velocity.

6. VERTICAL “VELOCITY”
COMPONENT
• Changes (due to gravity), does NOT cover equal
displacements in equal time periods.
Both the MAGNITUDE and DIRECTION
change. As the projectile moves up the
MAGNITUDE DECREASES and its direction
is UPWARD. As it moves down the
MAGNITUDE INCREASES and the direction
is DOWNWARD.

7. COMBINING THE
COMPONENTS
These components
produce what is called a
TRAJECTORY or path.
This path is PARABOLIC
in nature.
Component Magnitude Direction
Horizontal Constant Constant
Vertical Changes Changes

8. HORIZONTALLY
LAUNCHED PROJECTILES
Projectiles which have NO upward trajectory and NO
initial VERTICAL velocity.
0 /oyv m s
constantox xv v 

9. HORIZONTALLY LAUNCHED PROJECTILES
To analyze a projectile in 2 dimensions we need 2
equations. One for the “x” direction and one for the
“y” direction. And for this we use kinematic #2.
oxx v t
Remember, the velocity is
CONSTANT horizontally, so
that means the acceleration
is ZERO!
21
2
y gt
Remember that since the
projectile is launched
horizontally, the INITIAL
VERTICAL VELOCITY is equal
to ZERO.

10. HORIZONTALLY LAUNCHED PROJECTILES
Example:
A plane traveling with a
horizontal velocity of 100 m/s is
500 m above the ground. At
some point the pilot decides to
drop some supplies to
designated target below. (a)
How long is the drop in the air?
(b) How far away from point
where it was launched will it
land?
What do I
know?
What I want to
know?
vox=100 m/s t = ?
y = 500 m x = ?
voy= 0 m/s
g = -9.8 m/s/s
2 2
2
1 1500 ( 9.8)
2 2
102.04
y gt t
t t
    
   10.1 seconds
(100)(10.1)oxx v t   1010 m

11. VERTICALLY LAUNCHED PROJECTILES
Component Magnitude Direction
Horizontal Constant Constant
Vertical Decreases up, 0
@ top, Increases
down
Changes
Horizontal Velocity
is constant
Vertical
Velocity
decreases on
the way
upward
Vertical Velocity
increases on the
way down,
NO Vertical Velocity at the top of the trajectory.

12. VERTICALLY LAUNCHED PROJECTILES
Since the projectile was launched at a angle, the
velocity MUST be broken into components!!!
cos
sin
ox o
oy o
v v
v v




vo
vox
voy


13. VERTICALLY LAUNCHED
PROJECTILES
There are several things you
must consider when doing
these types of projectiles
besides using components. If it
begins and ends at ground
level, the “y” displacement is
ZERO: y = 0

14. VERTICALLY LAUNCHED PROJECTILES
You will still use kinematic #2, but YOU MUST use
COMPONENTS in the equation.
cos
sin
ox o
oy o
v v
v v




vo
vox
voy

oxx v t 21
2oyy v t gt 

15. EXAMPLE
A place kicker kicks a football with a velocity of 20.0 m/s and at
an angle of 53 degrees.
(a) How long is the ball in the air?
(b) How far away does it land?
(c) How high does it travel?
cos
20cos53 12.04 /
sin
20sin53 15.97 /
ox o
ox
oy o
oy
v v
v m s
v v
v m s



 

 
  53

16. EXAMPLE
A place kicker kicks a
football with a velocity
of 20.0 m/s and at an
angle of 53 degrees.
(a) How long is the ball
in the air?
What I know What I want
to know
vox=12.04 m/s t = ?
voy=15.97 m/s x = ?
y = 0 ymax=?
g = - 9.8
m/s/s
2 2
2
1 0 (15.97) 4.9
2
15.97 4.9 15.97 4.9
oyy v t gt t t
t t t
t
    
    
 3.26 s

17. EXAMPLE
A place kicker kicks a
football with a velocity
of 20.0 m/s and at an
angle of 53 degrees.
(b) How far away does it
land?
What I know What I want
to know
vox=12.04 m/s t = 3.26 s
voy=15.97 m/s x = ?
y = 0 ymax=?
g = - 9.8
m/s/s
(12.04)(3.26)oxx v t   39.24 m

18. SAMPLE PROBLEM:
A place kicker kicks a
football with a velocity
of 20.0 m/s and at an
angle of 53 degrees.
(c) How high does it
travel?
CUT YOUR TIME IN HALF!
What I know What I want
to know
vox=12.04 m/s t = 3.26 s
voy=15.97 m/s x = 39.24 m
y = 0 ymax=?
g = - 9.8
m/s/s
2
2
1
2
(15.97)(1.63) 4.9(1.63)
oyy v t gt
y
y
 
 
 13.01 m

19. BASICS STUDENTS SHOULD KNOW
1. What is a Projectile Motion?
2. What is a Projectile?
3. What is aTrajectory?
4. Why is Horizontal Velocity is constant all throughout in Projectile
Motion?
5. Why is Vertical velocity is zero at maximum height?
6. What is changing in Projectile Motion?
7. What is the difference between Half Projectile Motion and Full
Projectile Motion?
8. What is the difference Half-Time and Hang-Time?
9. Is there an acceleration along the horizontal in Projectile Motion?
10. Is there an acceleration along the vertical in Projectile Motion?
What is it?

20. HALF PROJECTILE MOTION

21. FULL PROJECTILE MOTION

22. PROJECTILE MOTION
HORIZONTAL
ax = o, Vox=Vx =
constant
Half projectile:
R= Voxt
Full Projectile:
X = Xo + Voxt
R = VoxT
VERTICAL
Half Projectile:
Voy=0
Y=1/2 ag t², use ag = -9.8 m/s²
Full Projectile:
@max pt/ht:
Vy=0, use ag = -9.8 m/s²
Y = Yo + Voyt + ½ agt²

23. OTHER KINEMATICS EQUATIONS TO
BE USED IN PROJECTILE MOTION
1. Vox = Vo cos ø
2. Voy = Vo sin ø
3. V = √Vx² + Vy²
4. Ø = tanˉ¹ (Voy/Vox) or Vy/Vx
5. Vy² = Voy² + 2 agY
6. Vy = Voy + agt

24. MORE EXAMPLES
1. A slingshot is used to launch a stone horizontally
from the top of a 20.0 meter cliff. The stone lands
36.o meters away.
a. At what speed was the stone launched? (17.82 m/s)
b. What is the speed and angle of impact? ( 26.64
m/s, -47.98 degrees)
2. A cannon fires a cannonball 500.0m downrange when
set at 45 degree angle. At what velocity does the
cannonball leave the cannon? (Answer: 70.0m/s)

25. EVALUATION
1. A punter in a football game kicks a ball from the goal
line at 60 degrees from the horizontal at 25.0 m/s
a. What is the hang time of the punt? (Ans: 4.41 s)
b. How far downfield does the ball land? (Ans: 55.2m)
2. A skier leaves the horizontal end of a ramp with a
velocity of 25.0m/s and lands 70.0 m from the base of
the ramp. How high is the end of the ramp from the
ground? (Answer: 38.5 m)

26. ASSIGNMENT
1. What is a Momentum
2. What is an Impulse
3. Bring the following
a. Block of Wood
b. Masking Tape
c. Protractor
d. Ruler/Meter Stick

27. QUOTE TO LIVE BY…
“Project, launch yourself
and be discovered…”
-YOURSTRULY-