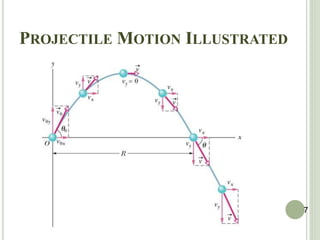
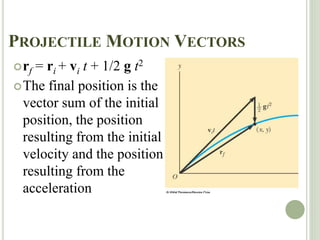
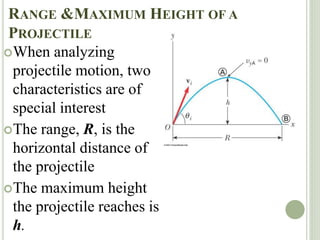
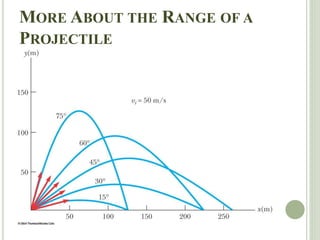
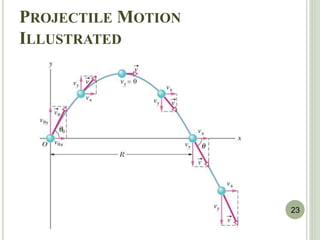
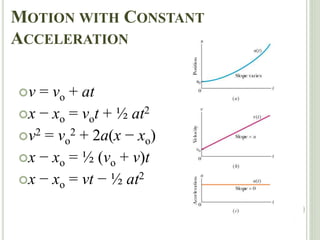
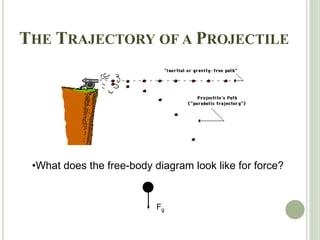
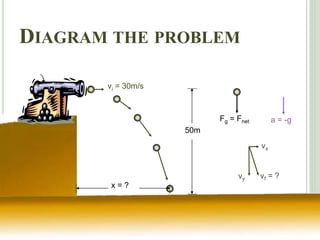
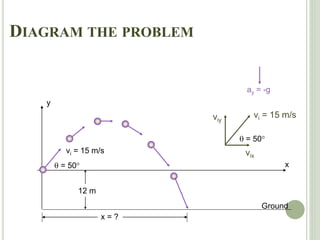
The document discusses projectile motion, which is two-dimensional motion under constant acceleration. Projectiles follow a parabolic trajectory due to gravity acting downward. The horizontal and vertical motions can be analyzed separately, with the horizontal motion having constant velocity and the vertical following equations for constant acceleration. Key aspects include calculating the maximum height, range, and landing location of a projectile given initial velocity and angle.

1. MOTION
IN TWO DIMENSIONS
(PROJECTILE MOTION)
Chapter04 from HRK.
Course code: 301
Course Title: Mechanics and properties of Matter
Course Incharge: SEHRISH INAM
Date: March08,2022

2. PROJECTILE MOTION
What is the path of a projectile as it moves
through the air?
 Parabolic?
 Straight up and down?
Yes, both are possible.
What forces act on projectiles?
 Only gravity, which acts only in the negative
y-direction.
 Air resistance is ignored in projectile motion.

3. MOTION IN TWO DIMENSIONS
Using + or – signs is not always sufficient
to fully describe motion in more than one
dimension
 Vectors can be used to more fully describe
motion
Still interested in displacement, velocity,
and acceleration
Will serve as the basis of multiple types of
motion in future chapters

4. GENERAL MOTION IDEAS
In two- or three-dimensional
kinematics, everything is the same as
as in one-dimensional motion except
that we must now use full vector
notation
 Positive and negative signs are no
longer sufficient to determine the
direction

5. PROJECTILE MOTION
An object may move in both the x and
y directions simultaneously
The form of two-dimensional motion
we will deal with is called projectile
motion
The object which is being moved in 2
dimension simultaneously is known
as projectile.

6. ASSUMPTIONS OF PROJECTILE
MOTION
The free-fall acceleration g is
constant over the range of motion
 And is directed downward
The effect of air friction is negligible
With these assumptions, an object in
projectile motion will follow a
parabolic path
 This path is called the trajectory

7. PROJECTILE MOTION ILLUSTRATED
7

8. VERIFYING THE PARABOLIC
TRAJECTORY
Reference frame chosen
 y is vertical with upward positive
Acceleration components
 ay = -g and ax = 0
Initial velocity components
 vxi = vi cosФ and vyi = vi sinФ

9. VERIFYING THE PARABOLIC TRAJECTORY,
CONT….
Displacements
 xf = vxi t = (vi cos Ф) t
 yf = vyi t + 1/2ay t2 = (vi sin Ф)t - 1/2 gt2
Combining the equations gives:
 This is in the form of y = ax – bx2 which is the
standard form of a parabola

10. ANALYZING PROJECTILE MOTION
Consider the motion as the superposition
of the motions in the x- and y-directions
The x-direction has constant velocity
 ax = 0
The y-direction is free fall
 ay = -g
The actual position at any time is given
by: rf = ri + vit + 1/2gt2

11. PROJECTILE MOTION VECTORS
rf = ri + vi t + 1/2 g t2
The final position is the
vector sum of the initial
position, the position
resulting from the initial
velocity and the position
resulting from the
acceleration

12. PROJECTILE MOTION DIAGRAM

13. PROJECTILE MOTION IMPLICATIONS
The y-component of the velocity is
zero at the maximum height of the
trajectory
The acceleration stays the same
throughout the trajectory
---------
------------------

14. RANGE &MAXIMUM HEIGHT OF A
PROJECTILE
When analyzing
projectile motion, two
characteristics are of
special interest
The range, R, is the
horizontal distance of
the projectile
The maximum height
the projectile reaches is
h.

15. HEIGHT OF A PROJECTILE,
EQUATION
The maximum height of the projectile
can be found in terms of the initial
velocity.
This equation is valid only for
symmetric motion

16. RANGE OF A PROJECTILE, EQUATION
The range of a projectile can be
expressed in terms of the initial
velocity vector:
This is valid only for symmetric
trajectory

17. MORE ABOUT THE RANGE OF A
PROJECTILE

18. RANGE OF A PROJECTILE, FINAL
The maximum range occurs at Ф =
45o
Complementary angles will produce
the same range
 The maximum height will be different
for the two angles
 The times of the flight will be
different for the two angles.

19. PROJECTILE MOTION – PROBLEM
SOLVING HINTS
Select a coordinate system
Resolve the initial velocity into x and y
components
Analyze the horizontal motion using
constant velocity techniques
Analyze the vertical motion using constant
acceleration techniques
Remember that both directions share the
same time.

20. NON-SYMMETRIC PROJECTILE MOTION
 Follow the general rules
for projectile motion
 Break the y-direction into
parts
 up and down or
 symmetrical back to initial
height and then the rest of
the height
 May be non-symmetric in
other ways

21. ACCELERATION IN DIFFERENT
FRAMES OF REFERENCE
The derivative of the velocity equation will
give the acceleration equation
The acceleration of the particle measured
by an observer in one frame of reference is
the same as that measured by any other
observer moving at a constant velocity
relative to the first frame.

22. PROJECTILE MOTION
Special case of 2-D motion
Horizontal motion: ax = 0 so vx = constant
Vertical motion: ay = g = constant so the
constant acceleration equations apply.
Assumptions:
 Horizontal and vertical motions are
independent of each other
 Air resistance (i.e., drag) can be
ignored.
22

23. PROJECTILE MOTION
ILLUSTRATED
23

24. MOTION WITH CONSTANT
ACCELERATION
v = vo + at
x − xo = vot + ½ at2
v2 = vo
2 + 2a(x − xo)
x − xo = ½ (vo + v)t
x − xo = vt − ½ at2
24

25. FREE-FALL ACCELERATION
EQUATIONS
If +y is vertically up, then the free-fall
acceleration due to gravity near Earth’s
surface is a = − g = − 9.8 m/s2.
v = vo − gt
y − yo = vot − ½ gt2
v2 = vo
2 − 2g(y − yo)
y − yo = ½ (vo + v)t
y − yo = vt + ½ gt2 25

26. THE TRAJECTORY OF A PROJECTILE
•What does the free-body diagram look like for force?
Fg

27. THE VECTORS OF PROJECTILE MOTION
What vectors exist in projectile
motion?
 Velocity in both the x and y directions.
 Acceleration in the y direction only.
vy (Increasing)
vx (constant)
ay = -9.8m/s2
ax = 0
Why is the velocity constant
in the x-direction?
•No force acting on it.
Why does the velocity
increase in the y-direction?
•Gravity.

28. EX. 1: LAUNCHING A PROJECTILE
HORIZONTALLY
A cannonball is shot horizontally
off a cliff with an initial velocity
of 30 m/s. If the height of the
cliff is 50 m:
 How far from the base of the cliff
does the cannonball hit the ground?
 With what speed does the
cannonball hit the ground?

29. DIAGRAM THE PROBLEM
50m
Fg = Fnet a = -g
vi = 30m/s
vf = ?
vx
vy
x = ?

30. STATE THE KNOWN & UNKNOWN
Known:
 vix = 30 m/s
 viy = 0 m/s
 a = -g = -9.81m/s2
 dy = -50 m
Unknown:
 dx at y = -50 m
 vf = ?

31. PERFORM CALCULATIONS (Y)
Strategy:
 Use reference table to find formulas you can use.
vfy = viy + gt
dy = viyt + ½ gt2
Note that g has been substituted for a and y for d.
 Use known factors such as in this case where the
initial velocity in the y-direction is known to be zero
to simplify the formulas.
vfy = viy + gt vfy = gt (1)
dy = viyt + ½ gt2 dy = ½ gt2 (2)

32. PERFORM CALCULATIONS (Y)
CONT…
(Use the second formula (2) first
because only time is unknown)
g
d
t
y
2

s
s
m
m
t 2
.
3
)
/
81
.
9
(
)
50
)(
2
(
2





33. PERFORM CALCULATIONS (Y)
CONT…..
Now that we have time, we can use
the first formula (1) to find the final
velocity.
 vfy = gt
 vy = (-9.8 m/s2)(3.2 s) = -31 m/s

34. PERFORM CALCULATIONS (X)
Strategy:
 Since you know the time for the vertical(y-
direction), you also have it for the x-direction.
 Time is the only variable that can transition
between motion in both the x and y directions.
 Since we ignore air resistance and gravity does not
act in the horizontal (x-direction), a = 0.
Choose a formula from your reference table
 dx = vixt + ½ at2
Since a = 0, the formula reduces to x = vixt
 dx = (30 m/s)(3.2 s) = 96 m from the base.

35. FINDING THE FINAL VELOCITY (VF)
We were given the initial x-component of
velocity, and we calculated the y-component at
the moment of impact.
Logic: Since there is no acceleration in the
horizontal direction, then vix = vfx.
We will use the Pythagorean Theorem.
vfx = 30m/s
vfy = -31m/s s
m
v
s
m
s
m
v
v
v
v
f
f
fy
fx
f
/
43
)
/
31
(
)
/
30
( 2
2
2
2






vf = ?

36. EX. 2: PROJECTILE MOTION ABOVE THE
HORIZONTAL
 A ball is thrown from the top of the Science Wing with
a velocity of 15 m/s at an angle of 50 degrees above
the horizontal.
 What are the x and y components of the initial velocity?
 What is the ball’s maximum height?
 If the height of the Science wing is 12 m, where will the ball
land?

37. DIAGRAM THE PROBLEM
y
x
vi = 15 m/s
 = 50°
ay = -g
Ground
12 m
x = ?
vi = 15 m/s
vix
viy
 = 50°

38. STATE THE KNOWN & UNKNOWN
Known:
 dyi = 12 m
 vi = 15 m/s
  = 50°
 ay = g = -9.8m/s2
Unknown:
 dy(max) = ?
 t = ?
 dx = ?
 viy = ?
 vix = ?

39. PERFORM THE CALCULATIONS (YMAX)
y-direction:
 Initial velocity: viy = visin
viy = (15 m/s)(sin 50°)
viy = 11.5 m/s
 Time when vfy = 0 m/s: vfy = viy + gt (ball at peak)
t = viy / g
t = (-11.5 m/s)/(-9.81 m/s2)
t = 1.17 s
 Determine the maximum height: dy(max) = yi + viyt + ½ gt2
dy(max) = 12 m + (11.5 m/s)(1.17 s) + ½ (-9.81 m/s2)(1.17
s)2
dy(max) = 18.7 m
vi = 15 m/s
vxi
vyi
 = 50°

40. PERFORM THE CALCULATIONS (T)
Since the ball will accelerate due to gravity over
the distance it is falling back to the ground, the
time for this segment can be determined as
follows
 Time from peak to when ball hits the ground:
From reference table: dy(max) = viyt + ½ gt2
Since yi can be set to zero as can viy,
t = 2* dy(max)/g
t = 2(-18.7 m)/(-9.81 m/s2)
t = 1.95 s
 By adding the time it takes the ball to reach its
maximum height (peak) to the time it takes to reach
the ground will give you the total time.
ttotal = 1.17 s + 1.95 s = 3.12 s



41. PERFORM THE CALCULATIONS (X)
x-direction:
 Initial velocity: vix = vicos
vix = (15 m/s)(cos 50°)
vix = 9.64 m/s
 Determine the total distance: x = vixt
dx = (9.64 m/s)(3.12 s)
dx = 30.1 m
vi = 15 m/s
vxi
vyi
 = 50°

42. ANALYZING MOTION IN THE X AND Y
DIRECTIONS INDEPENDENTLY.
x-direction y-direction
dx = vix t = vfxt dy = ½ (vi + vf) t
dy = vavg t
vix = vicos vf = viy + gt
dy = viyt + ½g(t)2
vfy
2 = viy
2 + 2gdy
viy = visin