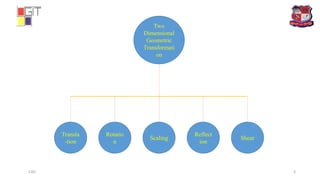
This document discusses various 2D geometric transformations including translation, rotation, scaling, reflection, and shear. It provides the mathematical formulas to perform each transformation using homogeneous coordinates and matrix representations. It also describes how to perform a composite transformation using multiple basic transformations sequentially, such as translating, rotating and translating again. Finally, it includes an example of rotating a triangle about two different points to demonstrate composite transformations.

1. Computer Aided Design (2161903)
Active Learning Assignment
Topic: Two Dimensional Geometric Transformation
Division:-Mechanical 6th D (D3)
Guided by: Prof. Dhaval P. Patel
Student name: Enrollment no.
Vasani Japan R. 150123119056
CAD 1

2. Contents
 Two Dimensional Geometric Transformation
• Translation
• Rotation
• Scaling
• Reflection
• Shear
 Homogeneous Coordinates
 Composite Transformation
 Example
CAD 2

3. Two
Dimensional
Geometric
Transformati
on
Shear
Reflect
ion
Transla
-tion
Rotatio
n
Scaling
CAD 3

4. Translation
xtxx '
ytyy '
x
y
p
P’
T
x
y
T
Translation transformation
• Translation vector or shift vector T = (tx, ty)
• Rigid-body transformation
• Moves objects without deformation
CAD 4

5. Rotation
x
y
P(x,y)
P’ (x’,y’)
r𝜽
 Consider rotation of a point about origin
 Let point P(x y) be rotated by an angle𝜽 about
origin O
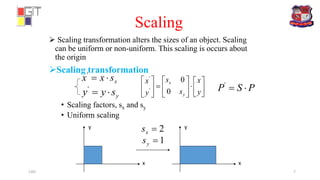
Rotation transformation
P = [x y]
= [rcos∅ rsin∅] ……(i)
Let the rotated point represented as:
P’ = [x’ y’]
= [rcos(𝜽+∅) rsin(𝜽+∅)]
= [rcos𝜽cos∅-rsin𝜽sin∅ rcos𝜽sin∅+rsin𝜽cos∅]
O
∅
CAD 5

6. Putting the value from equation (i)
= [x cos𝜽-ysin𝜽 xsin𝜽+ycos𝜽]
This can also represented as,
= [x y] [
𝑐𝑜𝑠𝜽 𝑠𝑖𝑛𝜽
−𝑠𝑖𝑛𝜽 𝑐𝑜𝑠𝜽
P’ = P . R
R =
𝑐𝑜𝑠𝜽 𝑠𝑖𝑛𝜽
−𝑠𝑖𝑛𝜽 𝑐𝑜𝑠𝜽
……….. (anticlockwise rotation)
R’=
𝑐𝑜𝑠𝜽 −𝑠𝑖𝑛𝜽
𝑠𝑖𝑛𝜽 𝑐𝑜𝑠𝜽
…………(clockwise rotation)
Rotation
CAD 6

7. Scaling
 Scaling transformation alters the sizes of an object. Scaling
can be uniform or non-uniform. This scaling is occurs about
the origin
Scaling transformation
• Scaling factors, sx and sy
• Uniform scaling
xsxx '
ysyy ' 

















y
x
s
s
y
x
y
x
0
0
'
'
PSP '
x
y
x
y2xs
1ys
CAD 7

8. Reflection
 Reflection is the same as obtaining a mirror of the original shape. This is an
important transformation and is used quite often as many engineered products
are symmetrical. The following transformation matrices as shown in below
I) Reflection about the x axis
II) Reflection about the y axis
III) Reflection relative to the coordinate origin
IV) Reflection about the line y = x
V) Reflection about the line y = -x
P’ = P . M
CAD 8

9. I) Reflection about the x axis
Reflection
CAD 9

10. II) Reflection about the y axis
Reflection
CAD 10

11. III) Reflection relative to the coordinate origin
Reflection
CAD 11

12. IV) Reflection about the line y = x
Reflection
CAD 12

13. V) Reflection about the line y = -x
Reflection
CAD 13

14. Shear
 The x-direction shear relative to x axis










100
010
01 xsh yshxx x '
yy '
If shx = 2:
CAD 14

15.  The x-direction shear relative to y = yref









 
100
010
1 refxx yshsh
)('
refx yyshxx 
yy '
If shx = ½ yref = -1:
1 1/2 3/2
Shear
CAD 15

16.  The y-direction shear relative to x = xref











100
1
001
refyy xshsh
xx '
yxxshy refy  )('
If shy = ½ xref = -1:
1
1/2
3/2
Shear
CAD 16

17. Homogeneous Coordinates
 The use of homogeneous coordinate system is vital when there are multiple operation
which include translation, as in this coordinate system; translation is also represented as
multiplication.
 Consider any point P(x y) which can be expressed as
Matrix representations
Translation =
),,(),( hyxyx hh
h
x
x h

h
y
y h
































1100
10
01
1
'
'
y
x
t
t
y
x
y
x
CAD 17

18. Homogeneous Coordinates
Scaling =
Rotation =































1100
00
00
1
'
'
y
x
s
s
y
x
y
x



















 











1100
0cossin
0sincos
1
'
'
y
x
y
x


CAD 18

19. Composite Transformation
Rotation about any selected pivot point (xr,yr)
• Translate – rotate - translate
CAD 19

20. 





















 











100
10
01
100
0cossin
0sincos
100
10
01
r
r
r
r
y
x
y
x















100
sin)cos1(cossin
sin)cos1(sincos


rr
rr
xy
yx
),,(),()(),(  rrrrrr yxRyxTRyxT 
Composite Transformation
CAD 20

21. Composite Transformation
 Scaling with respect to a selected fixed
position (xf,yf)
CAD 21

22. Composite Transformation
Translate-scale-translate


































100
10
01
100
00
00
100
10
01
r
r
y
x
r
r
y
x
s
s
y
x













100
)1(0
)1(0
yfy
xfx
sys
sxs
),,,(),(),(),( rrffffyxff yxyxSyxTssSyxT 
CAD 22

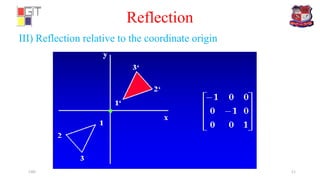
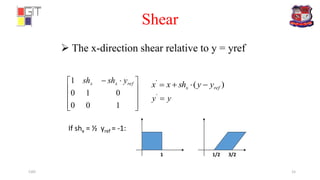
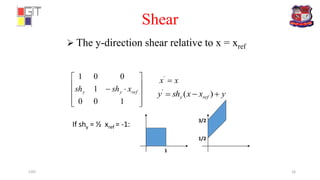
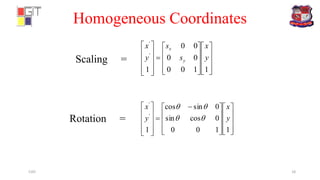
23. Example:- Perform a 45° rotation of a triangle A(0,0), B(1,1), C(5,3),
(i) about the origin and
(ii) about the point P(-1,-1)
Solution:-
(i) [T] = [A B C] [R]
=
0 0 1
1 1 1
5 2 1
.
𝑐𝑜𝑠𝜃 𝑠𝑖𝑛𝜃 0
−𝑠𝑖𝑛𝜃 𝑐𝑜𝑠𝜃 0
0 0 1
When, θ = 45°
[T] =
0 0 1
1 1 1
5 2 1
.
0.707 0.707 0
−0.707 0.707 0
0 0 1
=
0 0 1
0 1.414 1
2.121 4.949 1
So A’ (0,0), B’ (0,1.414), C’ (2.121,4.949)
CAD 23

24. (ii) [T] = [A B C] [Translation] [Rotation] [Inverse translation]
[T] = [A B C] [T] [R] [𝑇−1
]
=
0 0 1
1 1 1
5 2 1
.
1 0 0
0 1 0
1 1 1
.
𝑐𝑜𝑠45° 𝑠𝑖𝑛45° 0
−𝑠𝑖𝑛45° 𝑐𝑜𝑠45° 0
0 0 1
.
1 0 0
0 1 0
−1 −1 1
=
1 1 1
2 2 1
6 3 1
.
0.707 0.707 0
−0.707 0.707 0
0 0 1
.
1 0 0
0 1 0
−1 −1 1
=
0 1.414 1
0 2.828 1
2.121 6.363 1
.
1 0 0
0 1 0
−1 −1 1
=
−1 0.414 1
−1 1.828 1
1.121 5.363 1
A” (-1, 0.414), B” (-1, 1.828), C” (1.121, 5.363)CAD 24

25. CAD 25