This document provides an overview of angle modulation techniques, specifically phase modulation (PM) and frequency modulation (FM). It defines angle modulation as a non-linear process where the modulated wave does not resemble the message wave but the amplitude remains constant. Basic concepts of PM and FM are explained, showing how the carrier signal's phase or frequency varies with the message signal. Equations are provided to define PM and FM. The bandwidth requirements for both techniques are also summarized, with Carson's rule stated for FM bandwidth.

1. Angle Modulation
BY
Muhammad Uzair Rasheed
2009-CPE-03
UCE&T BZU MULTAN

2. Contents
 Properties of Angle (exponential) Modulation
 Types
 Phase Modulation
 Frequency Modulation

3. Properties
 Angle Modulation: A non-linear process:-
– Modulated wave does not look like message wave
– Amplitude of an exponentially modulated wave is constant
Therefore, regardless of message signal the average transmitted power is
1 2
P Ac
2
– It is less sensitive to noise

4. Basic Concept
 First introduced in 1931
A sinusoidal carrier signal is defined as: c(t ) Ac cos [ c t c (t )]
For un-modulated carrier signal the total instantaneous angle is:
c (t ) ct c (t )
Thus one can express c(t) as: c(t ) Ac cos c (t ) Ac Re [e j c (t )
]
Thus:
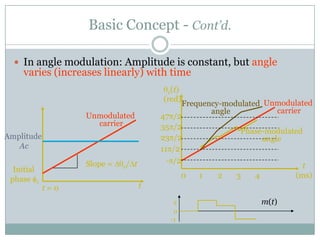
• Varying the frequency fc Frequency modulation
• Varying the phase c Phase modulation

5. Basic Concept - Cont’d.
 In angle modulation: Amplitude is constant, but angle
varies (increases linearly) with time
c(t)
(red)
Frequency-modulated Unmodulated
angle carrier
Unmodulated 47 /2
carrier 35 /2
Phase-modulated
Amplitude 23 /2 angle
Ac 11 /2
Slope = - /2
c/ t t
Initial
phase c 0 1 2 3 4 (ms)
t=0 t
2 m(t)
0
-1

6. Phase Modulation (PM)
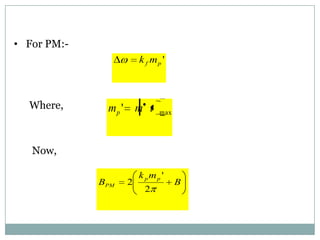
PM is defined If c (t ) K p m(t ) K p 1800
Thus c(t ) PM Ac cos [ c t K p m(t )]
Where Kp is known as the phase modulation index
Instantaneous phase i (t ) K p m(t )
i(t
Ac )
Instantaneous frequency
c(t)
c(t)
d c (t )
c(t) i (t ) c c (t )
dt
Rotating Phasor diagram

7. Frequency Modulation (FM)
The instantaneous frequency is; i (t ) c K f m(t )
Where Kf is known as the frequency modulation index.
Instantaneous phase
Note that
c (t ) K f m (t )
t
Integrating
i (t ) c c (t ) c (t ) ct K f m(t ) dt 0
0
t
Substituting c(t) in c(t) results in: c(t ) FM Ac cos[ ct K f m(t ) dt ]
0

8. Bandwidth of Angle modulation
• For FM:-
1
BFM 2k f m p 8 B
2
BFM 2 f 2B
k f mp
Frequency deviation= f
2
k f mp

9. • Deviation Ratio:-
f
B
• Carson’s Rule:-
BFM 2B 1
Note : Deviation ratio is also called modulation index

10. • For PM:-
k f mp '
Where, mp ' m t max
Now,
k pmp '
BPM 2 B
2

11. THANKS