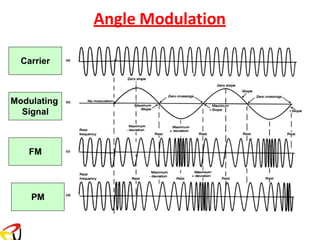
This document discusses angle modulation, focusing on frequency modulation (FM) and phase modulation (PM), detailing their definitions, equations, and relationships between the modulating signals and carrier frequencies. It emphasizes the concepts of instantaneous frequency and phase deviations, modulation indices, and bandwidth requirements for narrowband and wideband FM. Additionally, examples illustrate the practical applications and calculations related to these modulation techniques.

1. Lecture 7
Angle Modulation:
Frequency Modulation (FM)
Phase Modulation (PM)

2. Remember

3. Remember: Phase Shift

4. Angle Modulation

5. Angle Modulation
Radar

6. Angle Modulation
Carrier
Modulating
Signal
FM
PM

7. Angle Modulation
The carrier signal is represented by:
c(t) = Ac cos(2fct)
is the carrier amplitude
is the carrier frequency
where Ac
fc
Types of Angle Modulation
Phase Modulation
(PM)
Frequency Modulation
(FM)
Wide band FM Narrow band FM

8. Angle Modulation: Definitions
dt dt
dt dt
i c
i c
- The instantaneous frequency
2 2
:  (t) =
d (t)
=  +
d(t)
−The instantaneous radian frequency
: f (t) =
1 d (t)
= f +
1 d(t)
dt
i i
2 dt
 (t) =
d
(t) or f (t) =
1 d
(t)
- The instantaneous phase:(t) = ct +(t)
-The relationship between the instantaneous phase and the
instantaneous frequency is given by :
t t
(t) = i (t)dt or (t) = 2 fi (t)dt
0 0

9. Angle Modulation: Definitions
Maximum phase deviation : max(t)




2 dt
Maximum frequency deviation= Δf = max 1 d(t)
Theinstantaneous phasedeviation :(t)
2 dt
Theinstantaneous frequency deviation :
1 d(t)

10. Phase Modulation
Phase Modulation (PM): is that form of angle modulation
in which the instantaneous phase  (t) is varied linearly
with the message signal m(t) as:
(t) = ct + kpm(t)
s(t) = Accos[ct + kpm(t)]
The phase modulated signal s(t)is described in time domain by :
kp representsthe phase sensitivityof the modulator in [rad/volt]
m(t)is the modulating signal in [volt].
where:

11. Phase Modulation
Phase Modulation (PM):
s(t) = Ac cos[ct + kpm(t)]
The instantaneous phase deviation of the carrier
is proportional to the message amplitude.
Maximum phase deviation : max(t)= kp maxm(t)
Theinstantaneous phase deviation :(t) =kpm(t)

12. Frequency Modulation
Frequency Modulation (FM): is that form of angle modulation in
which the instantaneous frequency fi (t) is varied linearly with
the message signal m(t) as:
fi (t) = fc + kf m(t)
where: kf represents the frequency senstivity of the modulator in[Hz/volt]
m(t)is the modulating signal in[volt].
In FM, the instantaneous phase is givenby:
t
(t) = ct + 2kf  m()d
0
The frequency modulated signal s(t) is described in time domain by:
t
s(t) = Accos[ct + 2kf  m()d]
0

13. Frequency Modulation
Frequency Modulation (FM):
t
s(t) = Ac cos[ct + 2kf  m()d]
0
The instantaneous frequency deviation =
1d(t)
dt
2 dt
t
= kf m(t )
The instantaneous frequency deviation of the carrier
is proportional to the message amplitude.


 
d2 kf m()d 
=
1 0
2

14. Frequency Modulation
= kf max
m(t)
Maximum frequency deviation represents the maximum
of the instantaneous frequency of the FM signal
from the carrier frequency.

 
Maximum frequency deviation= f = max 1 d(t)

2 dt

15. Properties of Frequency Modulation
-As the modulating signal amplitude increases, the
carrier frequency increases and vise versa.
-Maximum frequency deviation is the maximum
change in the carrier frequency produced by the
modulating signal.
-The Maximum frequency deviation is proportional
to the amplitude of the modulating signal.

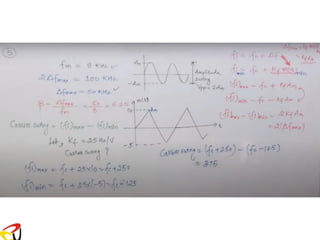
16. Example:
For a sinusoidal modulating signal defined by:
m(t) = Am cos(2fmt)
Find: - The modulated PM signal
- The instantaneous phase and the instantaneous angular
frequency of PM signal
- The PM signal is given by:
s(t) = Accos[ct +kpm(t)]
= Ac cos[ct + kp Am cos(2fmt)]
- The instantaneous phase:
(t) = ct + kp Am cos(2fmt)
- The instantaneous frequency:
dt
m m p m
i c
 (t) =
d (t)
=  − A  k sin( t)

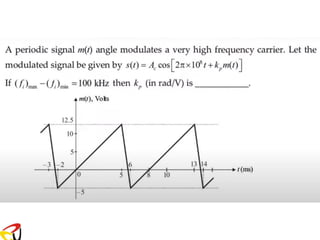
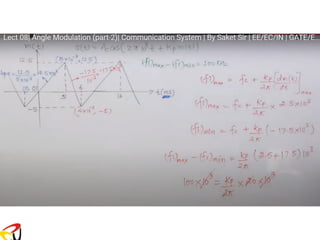
17. FM with Single Tone Modulating Signal
Consider a sinusoidal modulating signal defined by:
m(t) = Am cos(2fmt)
The instantaneous frequency of the FM signal is given by:
fi (t) = fc + kf Am cos(2fmt)
= fc + f cos(2fmt)
where f = k f Am is the maximum frequencydeviation
The FM signal is given by:
f
s(t) = Ac cos[ct +
f m
sin( t)]
m
= Ac cos[ct +  sin(mt)] (1)
0
t
s(t) = Ac cos[ct + 2kf m()d]

18. FM with Single Tone Modulating Signal
is the modulation index of the FM signal.
Physically, from (1), the parameter  represents the maximum
phase deviation of the FM signal, that is, the maximum
deviation (departure) of theangle(t)from theangle 2fct of the
unmodulated carrier.
f
m
m
Δf = β f
β =
Δf
s(t) = Ac cos[ct +  sin(mt)] (1)
where

19. PM with Single Tone Modulating Signal
Thesame analysis is valid for PM signal and the
modulating signal in PM is :
s(t) = Ac cos[ct + kp Am cos(mt)]
= Ac cos[ct +  cos(mt)]
Where  is the modulation index of PM signal measured in
rad.
 =kp Am [rad]

20. Determine whether the given signals are PM or FM
s(t) = Ac cos[ct +  sinmt]
s(t) = Ac cos[ct +  cosmt]

37. FM with Single Tone Modulating Signal
Depending on the value of the modulation index we have
two cases of frequency modulation
Narrowband FM
 1
Wideband FM
 1
Now, We need to investigate the bandwidth of FM

38. Narrowband FM (NBFM)

39. Narrowband FM (NBFM)
Which is similar to the AM signal which is given by:
The difference between the two equations (AM & NBFM) is the–ve
sign in the last term. Thus the NBFM requires the same transmission
bandwidth as AM.
The transmission bandwidth of the NBFM
is similar to the AM
BT = 2 f
m
since

40. Generation of Narrowband FM
m(t) = Am cos(2fmt)
m
m
Am
sin( t)
2f
m( )d =

sin(
A A k
c
m
m
c m f
sin( t)  t)
2f

41. Wideband FM (WBFM)
Now we determine the spectrum of the single tone FM signal for an
arbitrary value of the modulation index 
 
envelopeof FM signal.
is the complex
c
c
c
where c(t) = A e
c
e 
A eJ(ct +  sin(mt))
= Re
c(t) e 
= Re
(A e
= Re
s(t)= Ac cos(ct +  sin(mt)
J sin(mt)) Jct
Jct
J sin(mt))

42. Wideband FM (WBFM)
Where:

43. Wideband FM (WBFM)
Bessel function

44. Wideband FM (WBFM)

46. contained in the bandwidth
Transmission Bandwidth of FM Signals
In theory, an FM signal contains an infinite number of side frequencies so that
the bandwidth required to transmit such a signal is similarly infinite in extent.
✓It can be shown that 98 percent of the normalized total signal power is
 1 BW  2(1+ )fm
 BW  2 fm Hz
BW  2(1+)fm Hz
NARROW-BAND ANGLE-MODULATED
SIGNALS
WIDE-BAND ANGLE-MODULATED
SIGNALS
value of β<0.2 is
to satisfy this
✓Usually a
sufficient
condition.
f
m
m
m
m
BW 2()f 2
f
 f =2f Hz
 1BW 2(1+)f
Carson’s rule
This expression can
represents the general
case where fm
is the max.
frequency in the signal
The larger the modulation
Index, the larger the
bandwidth

47. Transmission Bandwidth of FM Signals
Another form of FM Bandwidth:

48. Example:

49. Example (Cont.)

B = 2(n fm )

B = 2(210kHz) = 40 kHz
B = 2(1 + 1) 10 kHz = 40 kHz
BW  2(1+ )fm Hz

50. Example (Cont.)
Calculate the magnitudes ????

51. Transmitted Power of WBFM
Since
T
T
2
2
2
2
1
2
2
1
Note this can be deduced easily (from the three form of representation of bandpass signals) as :
c
c
=
1
 A = A
c
c(t)  where c(t) = A e j(t)
T
P = 

53. Spectrum of WBFM
Spectrum of WBFM

54. − (fc − 3 fm ))+ J 3 ( ) (f + (fc − 3 fm ))
− (fc − 4 fm ))+ J − 4 ( ) (f + (fc − 4 fm )) +
.
.
.
2
2
2
2
2
2
2
2
− 4
− 3
− 2
− (fc − 2 fm ))+ J ( ) (f + (fc − 2 fm ))
− 2
+ Ac
J
+ Ac
J
+ Ac
J ( ) (f
( ) (f
( ) (f
−1 c m −1 c m
3
= 
2 c m 2 c m
 (f − (f + 2 f ))+ J ( ) (f + (f + 2 f ))
J ( )
1 c m 1 c m
 (f − (f + f ))+ J ( ) (f + (f + f ))
J ( )
+
+
+


n = − 
J n ( ) (f − (fc + nfm ))+  (f + (fc + nfm ))

sFM (t )= Ac  J n ( )cos(2fc t + 2nfm t )
n = − 
c
+
A
J ( )(f − (f − f ))+ J ( )(f + (f − f ))
c
c
c
o c o c
c
2
A
2
A
FM
S (f )=
Ac
A
A
+
Ac
J ( ) (f
4
J ( )(f − (fc + 3 fm ))+ J3 ( )(f + (fc + 3 fm ))
− (fc + 4 fm ))+ J 4 ( ) (f + (fc + 4 fm )) +
J ( ) (f − f )+ J ( ) (f + f )
n = 2
n = 1
n = 0
n = 3
n = 4
n = -2
n = -1
n = -3
n = -4

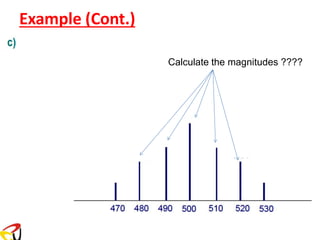
55. 0 1 0 0 2 0 0 3 0 0 7 0 0 8 0 0 9 0 0 1 0 0 0
0 . 5
0
1 . 5
1
2
3 . 5
3
2 . 5
4
4 . 5
5
XF
M(f)
4 0 0 5 0 0 6 0 0
F R E Q U E N C Y [ H z ]
Ac =10V
c
fm = 50 [Hz]
f = 500 [Hz]
2 2
c
o
A 10
J (2) = 0.239 =1.14
2 2
A 10
J1(2) c
= 0.5767 = 2.835
2
c
= 0.3528 =1.764
2 2
A 10
J (2)
2
= 0.1289 = 0.644
2 2
c
A 10
J (2)
 = 2
0 1 0 0 2 0 0 3 0 0 7 0 0 8 0 0 9 0 0 1 0 0 0
0
0 . 5
1
1 . 5
2
2 . 5
3
3 . 5
4
4 . 5
5
XF
M(f)
4 0 0 5 0 0 6 0 0
F R E Q U E N C Y [ H z ]
 = 0.5
2 2
= 0.9385 = 4.6955
c
o
A 10
J (0.5)
1
= 0.2423 =1.215
2 2
c
A 10
J (0.5)
2 2
2
c
A 10
J (0.5) = 0.03060 = 0.1530

56. Spectrum of WBFM
(1)The spectrum of an FM signal contains a carrier component
and an infinite set of sideband frequencies located
symmetrically on either side of the carrier at frequency
separation of fm ,2 fm ,3 fm ,...
(2) For the special case of  1 , Only the Bessel
coefficients J0 () and J1() have significant values so that the
spectrum of the FM is composed of a carrier and a single
pair of side frequencies at fc  fm

57. (3) Unlike the AM signal, the amplitude of the
carrier component varies with the modulation
index

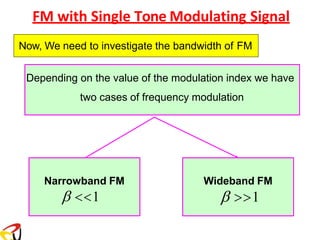
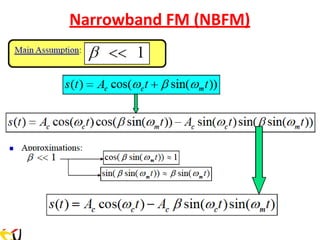
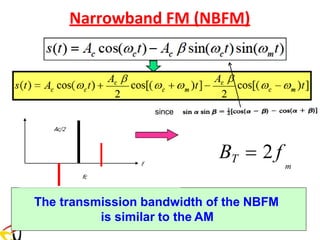
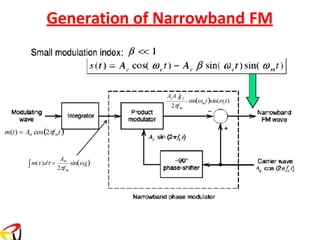
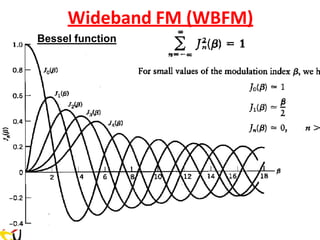
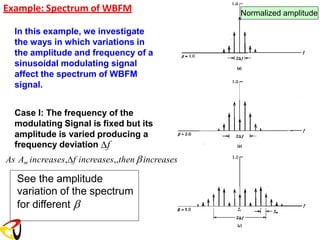
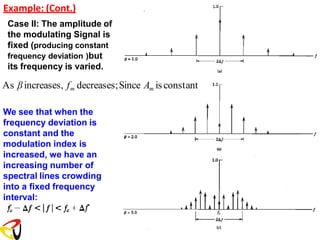
58. Remember: FM with Single Tone Modulating Signal
is the modulation index of the FM signal.
f = kf Am
Am is the amplitude of the modulating signal
where
m
m
Δf = β f
f
β =
Δf
s(t) = Ac cos[ct +  sin(mt)] (1)

59. Example: Spectrum of WBFM
See the amplitude
variation of the spectrum
for different 
Normalized amplitude
In this example, we investigate
the ways in which variations in
the amplitude and frequency of a
sinusoidal modulating signal
affect the spectrum of WBFM
signal.
Case I: The frequency of the
modulating Signal is fixed but its
amplitude is varied producing a
frequency deviation f
As Am increases,f increases,,then  increases

60. Example: (Cont.)
Case II: The amplitude of
the modulating Signal is
fixed (producing constant
frequency deviation )but
its frequency is varied.
As βincreases, fm decreases;Since Am is constant
We see that when the
frequency deviation is
constant and the
modulation index is
increased, we have an
increasing number of
spectral lines crowding
into a fixed frequency
interval:

61. Example (Cont.):
approaches infinity, the bandwidth of the
That is when 
FM signal approaching the limiting value of 2f which is an
important point to keep in mind for later discussion.

62. Difference between AM and Angle Modulation
(1)Zero crossings (instants of time at which a waveform
changes from a negative to a a positive value) no longer
have a perfect regularity in their spacing.
(2)The envelope of FM or PM signal is constant (equal to the
carrier amplitude), where as the envelope of an AM signal
is dependent on the message signal.
(3)The FM signal s(t) is a nonlinear function of the modulating
signal m(t) which makes FM to be a nonlinear modulation
process.
(4)Unlike AM, the spectrum of an FM signal is not related in a
simple manner to that of the modulating signal, rather, its
analysis is much more difficult than that of an AM signal.

63. Advantages of FM over AM

64. Disadvantages of FM over AM

65. Generation of FM Signals:
Direct Method (Parameter Variation Method)
In this method, the carrier frequency is directly varied in
accordance with the input baseband signal, which is
performed using voltage controlled oscillator.
VCO
A cos(2f t + cx(t))
c c
x(t)

68. Generation of FM Signals:
Indirect Method NBFM WBFM
This method is preferred when the carrier frequency stability is
of major concern as in commercial radio broadcasting

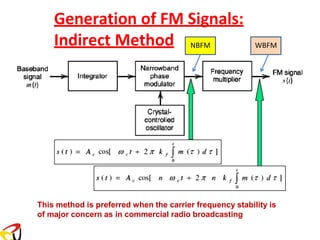
70. Frequency Multiplier
f
m
m
c c
= Ac cos[ct +  sin(
Remember : s(t) = A cos[ t +
f
sin( t)]

71. 

72. Example:

73. +VL
Received signal S ( t )
+VL
+VL
Limited signal SL ( t )
+VL
The received FM signal is passed to a BPF to remove
the out of band noise and then passed to a limiter to
remove any amplitude fluctuations due to noise. The next
step, the FM signal is demodulated to extract the signal.
Demodulation of FM Signals

75. Q 1
If m(t) = Sin(2000t) kf = 100 KHz/V and k p = 10 rad/V

85. Q. 7 What is the peak phase deviation?
Q. 8 Either the given signal is NB or WB?
Q. 9 What is the peak frequency deviation?