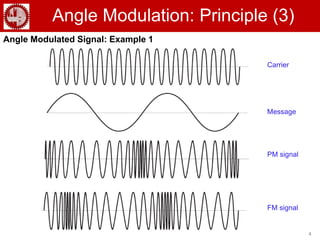
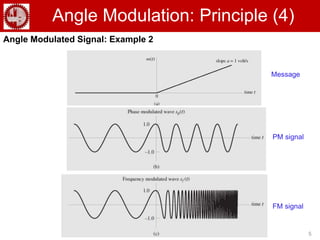
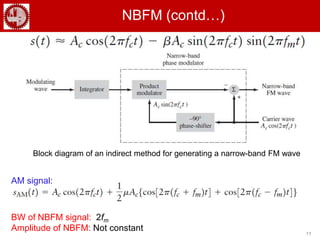
This document discusses angle modulation techniques, including phase modulation and frequency modulation. It provides examples of phase-modulated and frequency-modulated signals. Some key properties of angle modulated signals are described, such as their constancy of transmitted power and the nonlinearity of the modulation process. The relationship between phase modulation and frequency modulation is explained. Narrowband and wideband frequency modulation are also discussed, along with Carson's rule for calculating the bandwidth of frequency-modulated signals.

1. Communication Theory
Angle Modulation

2. 2
Angle Modulation: Principle (1)
 Angle of the carrier is varied according to the message
 Carrier amplitude remain constant
 Provides better discrimination against noise and interference than AM
 Required higher transmission bandwidth than that for AM
 Trade-off between channel bandwidth and noise performance
Angle modulated wave:
A simple case of an
unmodulated carrier:
Relationship between instantaneous phase and frequency:

3. 3
Angle Modulation: Principle (2)
Two common methods for angle modulation:
1. Phase Modulation (PM):
2. Frequency Modulation (FM):
kp = Phase sensitivity
factor (radians/volt)
Phase-modulated signal:
kf = Frequency sensitivity
factor (Hz/volt)
Frequency-modulated signal:

4. 4
Angle Modulation: Principle (3)
Angle Modulated Signal: Example 1
Carrier
Message
PM signal
FM signal

5. 5
Angle Modulation: Principle (4)
Angle Modulated Signal: Example 2
Message
PM signal
FM signal

6. 6
Properties of Angle Modulated Signal (1)
Property 1: Constancy of Transmitted Power
Amplitude of PM and FM waves is maintained at a constant value equal to the carrier
amplitude for all time t, irrespective of the sensitivity factors kp and kf
=> Average transmitted power of angle-modulated waves is a constant
Property 2: Nonlinearity of the Modulation Process
For m(t) = m1(t):
For m(t) = m2(t):
For m(t) = m1(t) + m2(t):
Consider PM (Prove the nonlinearity for FM by yourself):

7. 7
Properties of Angle Modulated Signal (5)
Property 3: Tradeoff of Increased Transmission Bandwidth for Improved
Noise Performance
 An important advantage of angle modulation over AM is the realization of improved
noise performance
 This advantage is due to the fact that the transmission of a message signal by
modulating the angle of a sinusoidal carrier wave is less sensitive to the presence of
additive noise than transmission by modulating the amplitude of the carrier
 The improvement in noise performance is, however, attained at the expense of a
corresponding increase in the transmission bandwidth requirement of angle
modulation
 In other words, the use of angle modulation offers the possibility of exchanging an
increase in transmission bandwidth for an improvement in noise performance.
 Such a tradeoff is not possible with amplitude modulation since the transmission
bandwidth of an amplitude-modulated wave is fixed somewhere between the
message bandwidth B and 2B Hz, depending on the type of modulation employed

8. 8
Relationship between PM and FM
FM:
PM:
 PM and FM are uniquely related to each other
 This means that the properties of PM can be deduced from those of FM and vice versa

9. 9
Frequency Modulation (FM) (1)
Consider a case of single-tone modulation:
Δf = Frequency Deviation (Hz)
= Maximum departure of fi of the FM wave from fc
β = Modulation Index
FM signal:

10. 10
Narrow-band FM (NBFM)
For small β:
1. NBFM (β is small compared to one radian):

11. 11
NBFM (contd…)
Block diagram of an indirect method for generating a narrow-band FM wave
AM signal:
BW of NBFM signal: 2fm
Amplitude of NBFM: Not constant

12. 12
Wide-band FM (WBFM)
2. WBFM (β is large compared to one radian):
Complex Envelope of s(t):
=> a periodic function of time with a fundamental frequency equal to fm

13. 13
WBFM (contd…)
Complex Fourier Coefficient
Jn(β) = nth order Bessel
function of the first kind and
argument β

14. 14
WBFM (contd…)
Thus,
=> S(f) consists of an infinite number of delta functions spaced at f = fc ± nfm

15. 15
WBFM (contd…)
Properties of FM for arbitrary β:
1. Jn(β) = (-1)n J-n(β) for all n
3.

16. 16
WBFM (contd…)
1. The spectrum of an FM wave contains a carrier component and an infinite set of
side frequencies located symmetrically on either side of the carrier at frequency
separations of fm, 2fm, 3fm, ….
2. For the special case of small β compared with unity, only the Bessel coefficients
J0(β) and J1(β) have significant values, so that the FM wave is effectively
composed of a carrier and a single pair of side-frequencies at fc±fm. This FM
signal is essentially the NBFM signal.
3. The amplitude of the carrier component varies with β according to J0(β). This
implies that the envelope of an FM wave is constant, so that the average power
of FM signal is constant.
Alternatively: Power of FM signal

17. 17
BW of FM Signals
Carson’s Rule







D
fWfBT
1
1222 W = BW of m(t)
Δf = kf m(t)|max
Single-tone
Multi-tone
 Theoretically, BW of FM wave is finite
 BW of FM signals is effectively limited to a finite number of significant side frequencies
Example: Commercial FM Broadcasting
In North America, the maximum value of frequency deviation Δf is fixed at 75 kHz
for commercial FM broadcasting by radio. Assume W = 15 kHz, which is typically
the “maximum” audio frequency of interest in FM transmission.
Carson’s rule: BT = 2∆f + 2W = 180 kHz