The document contains questions and answers related to mathematics for senior high school. It includes questions from past national exams from 2000-2020, as well as sample questions in both the old and new testing systems. The questions cover topics like functions, limits, derivatives, and graphing. The document is authored by a mathematics teacher and intended as a review guide for students.


![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2020: ημερήσια & εσπερινά
Ερωτήσεις (νέο σύστημα) Απαντήσεις
1. Για κάθε συνάρτηση 𝑓, ορισμένη, παραγωγίσιμη και γνησίως
αύξουσα στο ℝ, ισχύει 𝑓′(𝑥) > 0.
r Σ
r Λ
2. lim
𝑥→0
1
𝑥2𝜈+1 = +∞, για κάθε 𝜈 ∈ ℕ.
r Σ
r Λ
3. Αν 𝑓, 𝑔 είναι δύο συναρτήσεις με πεδία ορισμού Α και Β,
αντίστοιχα, τότε η 𝑔 ∘ 𝑓 ορίζεται, αν 𝑓(𝐴) ∩ 𝐵 ≠ ∅.
r Σ
r Λ
4. Η γραφική παράσταση της συνάρτησης 𝑓(𝑥) = √|𝑥|, 𝑥 ∈ ℝ
έχει άξονα συμμετρίας τον 𝑦′𝑦.
r Σ
r Λ
5. Η εικόνα 𝑓(Δ) ενός διαστήματος Δ μέσω μιας συνεχούς και μη
σταθερής συνάρτησης είναι πάντα διάστημα.
r Σ
r Λ
6. Δίνεται ότι η συνάρτηση 𝑓 παραγωγίζεται στο ℝ και ότι η
γραφική της παράσταση είναι πάνω από τον άξονα 𝑥′𝑥. Αν
υπάρχει κάποιο σημείο 𝐴(𝑥0, 𝑓(𝑥0)) της 𝐶𝑓, του οποίου η
απόσταση από τον άξονα 𝑥′𝑥 είναι μέγιστη (ή ελάχιστη), τότε σε
αυτό το σημείο η εφαπτομένη της 𝐶𝑓 είναι οριζόντια.
r Σ
r Λ
Ερωτήσεις (παλαιό σύστημα) Απαντήσεις
1. Για κάθε συνάρτηση 𝑓 με lim
𝑥→𝑥0
𝑓(𝑥) = 0, ισχύει ότι
lim
𝑥→𝑥0
1
𝑓(𝑥)
= +∞ ή lim
𝑥→𝑥0
1
𝑓(𝑥)
= −∞.
r Σ
r Λ
2. Αν lim
𝑥→𝑥0
𝑓(𝑥) = +∞, τότε 𝑓(𝑥) > 0 για κάθε 𝑥 κοντά στο 𝑥0. r Σ
r Λ
3. Αν μια συνάρτηση 𝑓 είναι συνεχής στο [𝛼, 𝛽], παραγωγίσιμη
στο (𝛼, 𝛽) και 𝑓′(𝑥) ≠ 0 για κάθε 𝑥 ∈ (𝛼, 𝛽), τότε 𝑓(𝛼) ≠ 𝑓(𝛽).
r Σ
r Λ
4. Για κάθε συνάρτηση 𝑓 που είναι παραγωγίσιμη και γνησίως
αύξουσα στο ℝ, ισχύει 𝑓′(𝑥) > 0 για κάθε 𝑥 ∈ ℝ.
r Σ
r Λ
2o ΓΕΛ Καματερού 2 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 3 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-3-320.jpg)
![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2020: επαναληπτικές ημερήσια & εσπερινά + ομογενείς
Ερωτήσεις (νέο σύστημα) Απαντήσεις
1. Κάθε συνάρτηση η οποία είναι συνεχής σε ένα σημείο του
πεδίου ορισμού της είναι και παραγωγίσιμη στο σημείο αυτό.
r Σ
r Λ
2. lim
𝑥→−∞
𝑒𝑥 = −∞. r Σ
r Λ
3. Για κάθε συνάρτηση 𝑓, το μεγαλύτερο από τα τοπικά μέγιστα
της 𝑓, εφόσον υπάρχουν, είναι το ολικό μέγιστο της 𝑓.
r Σ
r Λ
4. (ln|𝑥|)
′
= −
1
𝑥
, για κάθε 𝑥 < 0. r Σ
r Λ
5. Αν μια συνάρτηση 𝑓 είναι συνεχής σε ένα διάστημα Δ και δεν
μηδενίζεται σε αυτό, τότε η 𝑓 διατηρεί πρόσημο στο διάστημα Δ.
r Σ
r Λ
Ερωτήσεις (παλαιό σύστημα) Απαντήσεις
1. Για κάθε συνάρτηση 𝑓, η οποία είναι δύο φορές παραγωγίσιμη
και κυρτή στο ℝ, ισχύει 𝑓″(𝑥) > 0 για κάθε 𝑥 ∈ ℝ.
r Σ
r Λ
2. Για κάθε ζεύγος συναρτήσεων 𝑓, 𝑔 για τις οποίες ορίζονται οι
συναρτήσεις 𝑓 ∘ 𝑔 και 𝑔 ∘ 𝑓 ισχύει
𝑓 ∘ 𝑔 = 𝑔 ∘ 𝑓.
r Σ
r Λ
3. Για κάθε ζεύγος συναρτήσεων 𝑓, 𝑔 για τις οποίες υπάρχουν τα
όρια lim
𝑥→𝑥0
𝑓(𝑥), lim
𝑥→𝑥0
𝑔(𝑥) και 𝑓(𝑥) < 𝑔(𝑥) για κάθε 𝑥 κοντά στο
𝑥0, ισχύει
lim
𝑥→𝑥0
𝑓(𝑥) < lim
𝑥→𝑥0
𝑔(𝑥).
r Σ
r Λ
4. Αν μια συνάρτηση 𝑓 είναι συνεχής στο [𝛼, 𝛽], τότε η 𝑓 παίρνει
στο [𝛼, 𝛽], μια μέγιστη τιμή 𝑀 και μια ελάχιστη τιμή 𝑚.
r Σ
r Λ
5. Για κάθε 𝑥 ∈ ℝ − {0}, ισχύει (ln|𝑥|)′ =
1
𝑥
. r Σ
r Λ
2o ΓΕΛ Καματερού 3 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 4 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-4-320.jpg)

![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2018:ημερήσια & εσπερινά
Ερωτήσεις Απαντήσεις
1. Κάθε συνάρτηση 𝑓 ∶ ℝ → ℝ που είναι 1 − 1 είναι και γνησίως
μονότονη.
r Σ
r Λ
2. Η συνάρτηση 𝑓(𝑥) = ημ𝑥 με 𝑥 ∈ ℝ έχει μία μόνο θέση ολικού
μεγίστου.
r Σ
r Λ
3. Για κάθε παραγωγίσιμη συνάρτηση 𝑓 σε ένα διάστημα Δ, η
οποία είναι γνησίως αύξουσα, ισχύει 𝑓′(𝑥) > 0 για κάθε 𝑥 ∈ Δ.
r Σ
r Λ
4. Ισχύει lim
𝑥→0
1 − συν𝑥
𝑥
= 0.
r Σ
r Λ
5. Αν η 𝑓 είναι αντιστρέψιμη συνάρτηση, τότε οι γραφικές
παραστάσεις 𝐶 και 𝐶′ των συναρτήσεων 𝑓 και 𝑓−1 αντίστοιχα
είναι συμμετρικές ως προς την ευθεία 𝑦 = 𝑥.
r Σ
r Λ
6. Κάθε κατακόρυφη ευθεία έχει το πολύ ένα κοινό σημείο με τη
γραφική παράσταση μιας συνάρτησης 𝑓.
r Σ
r Λ
2018: επαναληπτικές ημερήσια & εσπερινά + ομογενείς
Ερωτήσεις Απαντήσεις
1. Για κάθε ζεύγος πραγματικών συναρτήσεων
𝑓, 𝑔 ∶ (0, +∞) → ℝ, αν ισχύει lim
𝑥→0
𝑓(𝑥) = +∞ και
lim
𝑥→0
𝑔(𝑥) = −∞, τότε lim
𝑥→0
[𝑓(𝑥) + 𝑔(𝑥)] = 0.
r Σ
r Λ
2. Η γραφική παράσταση μιας συνάρτησης 𝑓 ∶ ℝ → ℝ μπορεί να
τέμνει την ασύμπτωτή της.
r Σ
r Λ
3. Αν μια συνάρτηση 𝑓 ∶ ℝ → ℝ είναι 1 − 1 , τότε κάθε οριζόντια
ευθεία τέμνει τη γραφική παράσταση της 𝑓 το πολύ σε ένα σημείο.
r Σ
r Λ
4. Αν οι συναρτήσεις 𝑓 και 𝑔 έχουν πεδίο ορισμού το [0, 1] και
σύνολο τιμών το [2, 3], τότε ορίζεται η 𝑓 ∘ 𝑔 με πεδίο ορισμού το
[0, 1] και σύνολο τιμών το [2, 3]
r Σ
r Λ
2o ΓΕΛ Καματερού 5 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 6 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-6-320.jpg)
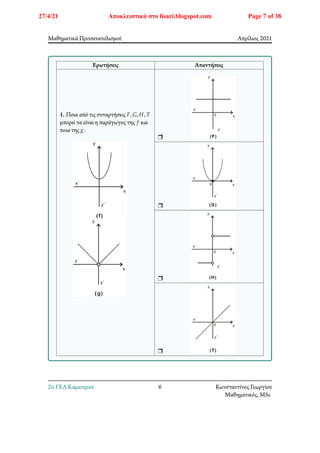
![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2017:ημερήσια & εσπερινά
Ερωτήσεις Απαντήσεις
1. Κάθε συνάρτηση 𝑓, η οποία είναι συνεχής στο 𝑥0 είναι
παραγωγίσιμη στο σημείο αυτό.
r Σ
r Λ
2. Για κάθε ζεύγος συναρτήσεων 𝑓 ∶ ℝ → ℝ και 𝑔 ∶ ℝ → ℝ, αν
lim
𝑥→𝑥0
𝑓(𝑥) = 0 και lim
𝑥→𝑥0
𝑔(𝑥) = +∞ τότε lim
𝑥→𝑥0
[𝑓(𝑥) ⋅ 𝑔(𝑥)] = 0.
r Σ
r Λ
3. Αν 𝑓, 𝑔 είναι δύο συναρτήσεις με πεδία ορισμού Α, Β
αντίστοιχα, τότε η 𝑔 ∘ 𝑓 ορίζεται αν 𝑓(𝐴) ∩ 𝐵 ≠ ∅.
r Σ
r Λ
4. Για κάθε συνάρτηση 𝑓 ∶ ℝ → ℝ που είναι παραγωγίσιμη και
δεν παρουσιάζει ακρότατα, ισχύει 𝑓′(𝑥) ≠ 0 για κάθε 𝑥 ∈ ℝ.
r Σ
r Λ
5. Αν 0 < 𝛼 < 1, τότε lim
𝑥→−∞
𝛼𝑥 = +∞. r Σ
r Λ
6. Η εικόνα 𝑓(Δ) ενός διαστήματος Δ μέσω μιας συνεχούς και μη
σταθερής συνάρτησης 𝑓 είναι διάστημα.
r Σ
r Λ
7. Αν lim
𝑥→𝑥0
𝑓(𝑥) = −∞, τότε 𝑓(𝑥) > 0 κοντά στο 𝑥0. r Σ
r Λ
2o ΓΕΛ Καματερού 7 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 8 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-8-320.jpg)
![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2017: επαναληπτικές ημερήσια & εσπερινά + ομογενείς
Ερωτήσεις Απαντήσεις
1. Για κάθε συνάρτηση 𝑓 η οποία είναι ορισμένη και δύο φορές
παραγωγίσιμη στο ℝ ισχύει 𝑓″(𝑥0) = 0, τότε το 𝑥0 είναι θέση
σημείου καμπής της 𝐶𝑓.
r Σ
r Λ
2. Μια συνάρτηση 𝑓 λέγεται γνησίως αύξουσα σε ένα διάστημα
Δ του πεδίου ορισμού της, αν υπάρχουν 𝑥1, 𝑥2 ∈ Δ με 𝑥1 < 𝑥2,
ώστε 𝑓(𝑥1) < 𝑓(𝑥2).
r Σ
r Λ
3. Αν ένα σημείο Μ(𝛼, 𝛽) ανήκει στη γραφική παράσταση μιας
αντιστρέψιμης συνάρτησης 𝑓, τότε το σημείο Μ′(𝛽, 𝛼) ανήκει
στη γραφική παράσταση 𝐶′ της 𝑓−1.
r Σ
r Λ
4. Για κάθε συνεχή συνάρτηση 𝑓 ∶ [𝛼, 𝛽] → ℝ, η οποία είναι
παραγωγίσιμη στο (𝛼, 𝛽), αν 𝑓(𝛼) = 𝑓(𝛽), τότε υπάρχει ακριβώς
ένα 𝜉 ∈ (𝛼, 𝛽) τέτοιο ώστε 𝑓′(𝜉) = 0.
r Σ
r Λ
Ερωτήσεις Απαντήσεις
1. Για κάθε συνεχή
συνάρτηση
𝑓 ∶ [𝛼, 𝛽] → ℝ,
αν ισχύει
𝑓(𝛼) ⋅ 𝑓(𝛽) > 0,
τότε
r η εξίσωση 𝑓(𝑥) = 0 δεν έχει λύση στο (𝛼, 𝛽).
r η εξίσωση 𝑓(𝑥) = 0 έχει ακριβώς μία λύση στο (𝛼, 𝛽).
r η εξίσωση 𝑓(𝑥) = 0 έχει τουλάχιστον δύο λύσεις στο (𝛼, 𝛽).
r δεν μπορούμε να έχουμε συμπέρασμα για το πλήθος των λύ-
σεων της εξίσωσης 𝑓(𝑥) = 0 στο (𝛼, 𝛽).
2o ΓΕΛ Καματερού 8 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 9 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-9-320.jpg)
![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2016: ημερήσια & εσπερινά
Ερωτήσεις Απαντήσεις
1. Αν οι συναρτήσεις 𝑓, 𝑔 έχουν όριο στο 𝑥0 και ισχύει
𝑓(𝑥) ≤ 𝑔(𝑥) κοντά στο 𝑥0, τότε lim
𝑥→𝑥0
𝑓(𝑥) ≤ lim
𝑥→𝑥0
𝑔(𝑥).
r Σ
r Λ
2. Κάθε συνάρτηση 𝑓, για την οποία ισχύει 𝑓′(𝑥) = 0 για κάθε
𝑥 ∈ (𝛼, 𝑥0) ∪ (𝑥0, 𝛽), είναι σταθερή στο (𝛼, 𝑥0) ∪ (𝑥0, 𝛽).
r Σ
r Λ
3. Μια συνάρτηση 𝑓 είναι 1 − 1, αν και μόνο αν, για κάθε
στοιχείο 𝑦 του συνόλου τιμών της, η εξίσωση 𝑦 = 𝑓(𝑥) έχει
ακριβώς μια λύση ως προς 𝑥.
r Σ
r Λ
4. Αν η 𝑓 είναι συνεχής στο [𝛼, 𝛽], τότε η 𝑓 παίρνει στο [𝛼, 𝛽],
μια μέγιστη τιμή Μ και μια ελάχιστη τιμή 𝑚.
r Σ
r Λ
5. lim
𝑥→0
ημ𝑥
𝑥
= 0 r Σ
r Λ
2o ΓΕΛ Καματερού 9 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 10 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-10-320.jpg)






![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2012: επαναληπτικες ημερήσια & εσπερινά + ομογενείς
Ερωτήσεις Απαντήσεις
1. Η γραφική παράσταση της συνάρτησης −𝑓 είναι συμμετρική,
ως προς τον άξονα 𝑥′𝑥, της γραφικής παράστασης της 𝑓.
r Σ
r Λ
2. Αν είναι 0 < 𝛼 < 1, τότε lim
𝑥→+∞
𝛼𝑥 = +∞. r Σ
r Λ
3. Αν μια συνάρτηση 𝑓 δεν είναι συνεχής σε ένα σημείο 𝑥0, τότε
δεν μπορεί να είναι παραγωγίσιμη στο 𝑥0.
r Σ
r Λ
4. Για την πολυωνυμική συνάρτηση
𝑃(𝑥) = 𝛼𝜈𝑥𝜈 + 𝛼𝜈−1𝑥𝜈−1 + ⋯ + 𝛼0 με 𝛼𝜈 ≠ 0 ισχύει:
lim
𝑥→+∞
𝑃(𝑥) = 𝛼0.
r Σ
r Λ
5. Αν μια συνάρτηση 𝑓 δεν είναι συνεχής σε ένα σημείο 𝑥0, τότε
δεν μπορεί να είναι παραγωγίσιμη στο 𝑥0.
r Σ
r Λ
6. Έστω μια συνάρτηση 𝑓 παραγωγίσιμη σε ένα διάστημα (𝛼, 𝛽),
με εξαίρεση ίσως ένα σημείο του 𝑥0, στο οποίο όμως η 𝑓 είναι
συνεχής. Αν 𝑓′(𝑥) > 0 στο (𝛼, 𝑥0) και 𝑓′(𝑥) < 0 στο (𝑥0, 𝛽), τότε
το 𝑓(𝑥0) είναι τοπικό ελάχιστο της 𝑓.
r Σ
r Λ
7. Αν είναι lim
𝑥→𝑥0
𝑓(𝑥) = −∞, τότε lim
𝑥→𝑥0
|𝑓(𝑥)| = +∞. r Σ
r Λ
8. Ισχύει (εφ𝑥)′ = −
1
συν2 𝑥
, 𝑥 ∈ ℝ − { 𝑥 | συν𝑥 = 0 }
r Σ
r Λ
9. Αν οι συναρτήσεις 𝑓 και 𝑔 είναι παραγωγίσιμες στο 𝑥0 και
𝑔(𝑥0) ≠ 0, τότε και η συνάρτηση
𝑓
𝑔
είναι παραγωγίσιμη στο 𝑥0
και ισχύει:
𝑓
𝑔
′
(𝑥0) =
𝑓′(𝑥0)𝑔(𝑥0) − 𝑓(𝑥0)𝑔′(𝑥))
[𝑔(𝑥0)]2
r Σ
r Λ
2o ΓΕΛ Καματερού 16 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 17 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-17-320.jpg)

![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2010: ημερήσια & εσπερινά
Ερωτήσεις Απαντήσεις
1. Έστω συνάρτηση 𝑓 συνεχής σε ένα διάστημα Δ και
παραγωγίσιμη στο εσωτερικό του Δ. Αν η 𝑓 είναι γνησίως
αύξουσα στο Δ, τότε η παράγωγός της δεν είναι υποχρεωτικά
θετική στο εσωτερικό του Δ.
r Σ
r Λ
2. Αν μια συνάρτηση 𝑓 είναι γνησίως φθίνουσα και συνεχής σε
ένα ανοικτό διάστημα (𝛼, 𝛽), τότε το σύνολο τιμών της στο
διάστημα αυτό είναι το διάστημα (Α, Β), όπου:
Α = lim
𝑥→𝛼+
𝑓(𝑥) και 𝐵 = lim
𝑥→𝛽−
𝑓(𝑥)
r Σ
r Λ
3. Ισχύει: (συν𝑥)′ = ημ𝑥, 𝑥 ∈ ℝ.
r Σ
r Λ
4. Αν lim
𝑥→𝑥0
𝑓(𝑥) < 0, τότε 𝑓(𝑥) < 0 κοντά στο 𝑥0. r Σ
r Λ
5. Το πεδίο ορισμού μιας συνάρτησης 𝑓 είναι το σύνολο 𝐴 των
τετμημένων των σημείων της γραφικής παράστασης 𝐶𝑓 της
συνάρτησης.
r Σ
r Λ
6. Για κάθε συνάρτηση 𝑓 παραγωγίσιμη σε ένα διάστημα Δ και
για κάθε πραγματικό αριθμό 𝑐, ισχύει ότι:
(𝑐 ⋅ 𝑓(𝑥))′ = 𝑓′(𝑥), για κάθε 𝑥 ∈ Δ.
r Σ
r Λ
7. Το σύνολο τιμών μιας συνεχούς συνάρτησης 𝑓 με πεδίο
ορισμού το κλειστό διάστημα [𝑚, 𝑀], όπου 𝑚 η ελάχιστη και 𝑀
η μέγιστη τιμή της.
r Σ
r Λ
8. Αν lim
𝑥→𝑥0
𝑓(𝑥) = +∞, τότε 𝑓(𝑥) < 0 κοντά στο 𝑥0. r Σ
r Λ
2o ΓΕΛ Καματερού 18 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 19 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-19-320.jpg)

![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2009: ημερήσια & εσπερινά
Ερωτήσεις Απαντήσεις
1. Μια συνάρτηση 𝑓 με πεδίο ορισμού Α λέμε ότι παρουσιάζει
(ολικό) ελάχιστο στο 𝑥0 ∈ 𝐴, όταν 𝑓(𝑥) ≥ 𝑓(𝑥0) για κάθε 𝑥 ∈ 𝐴.
r Σ
r Λ
2. lim
𝑥→0
συν𝑥 − 1
𝑥
= 1
r Σ
r Λ
3. Κάθε συνάρτηση 𝑓 συνεχής σε ένα σημείο του πεδίου ορισμού
της είναι και παραγωγίσιμη στο σημείο αυτό.
r Σ
r Λ
4. lim
𝑥→0
ημ𝑥
𝑥
= 0 r Σ
r Λ
5. Αν μία συνάρτηση 𝑓 είναι συνεχής στο κλειστό διάστημα
[𝛼, 𝛽] και παραγωγίσιμη στο ανοικτό διάστημα (𝛼, 𝛽), τότε
υπάρχει ένα τουλάχιστον 𝜉 ∈ (𝛼, 𝛽) τέτοιο, ώστε:
𝑓′(𝜉) =
𝑓(𝛽) − 𝑓(𝛼)
𝛽 − 𝛼
r Σ
r Λ
2o ΓΕΛ Καματερού 20 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 21 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-21-320.jpg)

![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2008: ημερήσια & εσπερινά
Ερωτήσεις Απαντήσεις
1. Αν μια συνάρτηση 𝑓 ∶ 𝐴 → ℝ είναι 1 − 1, τότε για την
αντίστροφη συνάρτηση 𝑓−1 ισχύει:
𝑓−1 𝑓(𝑥) = 𝑥, 𝑥 ∈ 𝐴 και 𝑓 𝑓−1(𝑦) = 𝑦, 𝑦 ∈ 𝑓(𝐴)
r Σ
r Λ
2. Μια συνεχής συνάρτηση 𝑓 διατηρεί πρόσημο σε καθένα από
τα διαστήματα στα οποία οι διαδοχικές ρίζες της 𝑓 χωρίζουν το
πεδίο ορισμού της.
r Σ
r Λ
3. Αν μια συνάρτηση 𝑓 είναι δύο φορές παραγωγίσιμη στο ℝ και
στρέφει τα κοίλα προς τα άνω, τότε κατ΄ ανάγκη θα ισχύει
𝑓″(𝑥) > 0 ∀𝑥 ∈ ℝ
r Σ
r Λ
4. Για κάθε 𝑥 ∈ ℝ ισχύει: (ημ𝑥)′ = − συν𝑥. r Σ
r Λ
5. Αν μια συνάρτηση 𝑓 είναι συνεχής σε ένα διάστημα Δ και δεν
μηδενίζεται σε αυτό, τότε αυτή ή θα είναι θετική για κάθε 𝑥 ∈ Δ ή
είναι αρνητική για κάθε 𝑥 ∈ Δ, δηλαδή διατηρεί πρόσημο στο
διάστημα Δ.
r Σ
r Λ
6. Αν μία συνάρτηση 𝑓 είναι:
• συνεχής στο κλειστό διάστημα [𝛼, 𝛽]
• παραγωγίσιμη στο ανοικτό διάστημα (𝛼, 𝛽) και
• 𝑓(𝛼) = 𝑓(𝛽)
τότε υπάρχει ένα, τουλάχιστον, 𝜉 ∈ (𝛼, 𝛽) τέτοιο, ώστε: 𝑓′(𝜉) = 0.
r Σ
r Λ
2o ΓΕΛ Καματερού 22 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 23 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-23-320.jpg)

![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2007: ημερήσια & εσπερινά
Ερωτήσεις Απαντήσεις
1. Έστω 𝑓 μια συνάρτηση συνεχής σε ένα διάστημα Δ και
παραγωγίσιμη σε κάθε εσωτερικό σημείο 𝑥 του Δ. Αν η
συνάρτηση 𝑓 είναι γνησίως αύξουσα στο Δ, τότε 𝑓′(𝑥) > 0 σε
κάθε εσωτερικό σημείο 𝑥 του Δ.
r Σ
r Λ
2. Αν η συνάρτηση 𝑓 είναι συνεχής στο 𝑥0 και η συνάρτηση 𝑔
είναι συνεχής στο 𝑥0, τότε η σύνθεση τους 𝑔 ∘ 𝑓 είναι συνεχής
στο 𝑥0.
r Σ
r Λ
3. Αν 𝛼 > 1 τότε lim
𝑥→−∞
𝛼𝑥 = 0 r Σ
r Λ
4. Μια συνάρτηση 𝑓 είναι 1 − 1, αν και μόνο αν κάθε οριζόντια
ευθεία (παράλληλη στον 𝑥′𝑥 ) τέμνει τη γραφική παράστασή της
το πολύ σε ένα σημείο.
r Σ
r Λ
5. Αν υπάρχει το όριο της συνάρτησης 𝑓 στο 𝑥0 ∈ ℝ και
lim
𝑥→𝑥0
𝑓(𝑥) < 0, τότε 𝑓(𝑥) < 0 κοντά στο 𝑥0.
r Σ
r Λ
6. Αν 𝑓 είναι συνεχής συνάρτηση στο [𝛼, 𝛽], τότε η 𝑓 παίρνει
στο [𝛼, 𝛽] μια μέγιστη τιμή 𝑀 και μια ελάχιστη τιμή 𝑚.
r Σ
r Λ
7. Έστω η συνάρτηση 𝑓(𝑥) = ημ𝑥 με πεδίο ορισμού το ℝ. Τότε,
𝑓′(𝑥) = − συν𝑥, για κάθε 𝑥 ∈ ℝ.
r Σ
r Λ
2o ΓΕΛ Καματερού 24 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 25 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-25-320.jpg)
![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2007: επαναληπτικές ημερήσια & εσπερινά + ομογενείς
Ερωτήσεις Απαντήσεις
1. Η εικόνα 𝑓(Δ) ενός διαστήματος Δ μέσω μιας συνεχούς
συνάρτησης 𝑓 είναι διάστημα.
r Σ
r Λ
2. Αν μια συνάρτηση 𝑓 είναι γνησίως αύξουσα και συνεχής σε ένα
ανοικτό διάστημα (𝛼, 𝛽), τότε το σύνολο τιμών της στο διάστημα
αυτό είναι το διάστημα (Α, Β) όπου Α = lim
𝑥→𝛼+
𝑓(𝑥) και
Β = lim
𝑥→𝛽−
𝑓(𝑥).
r Σ
r Λ
3. Έστω δύο συναρτήσεις 𝑓, 𝑔 ορισμένες σε ένα διάστημα Δ. Αν
οι 𝑓, 𝑔 είναι συνεχείς στο Δ και 𝑓′(𝑥) = 𝑔′(𝑥) για κάθε εσωτερικό
σημείο 𝑥 του Δ, τότε ισχύει 𝑓(𝑥) = 𝑔(𝑥) για κάθε 𝑥 ∈ Δ.
r Σ
r Λ
4. Η γραφική παράσταση της συνάρτησης −𝑓 είναι συμμετρική,
ως προς τον άξονα 𝑥′𝑥, της γραφικής παράστασης της 𝑓.
r Σ
r Λ
5. Αν 𝑓, 𝑔, ℎ είναι τρεις συναρτήσεις και ορίζεται η ℎ ∘ (𝑔 ∘ 𝑓),
τότε ορίζεται και η (ℎ ∘ 𝑔) ∘ 𝑓 και ισχύει ℎ ∘ (𝑔 ∘ 𝑓) = (ℎ ∘ 𝑔) ∘ 𝑓.
r Σ
r Λ
6. Οι πολυωνυμικές συναρτήσεις βαθμού μεγαλύτερου ή ίσου του
2 έχουν ασύμπτωτες.
r Σ
r Λ
7. Ισχύει: lim
𝑥→0
συν𝑥 − 1
𝑥
= 1.
r Σ
r Λ
8. Αν μια συνάρτηση 𝑓 δεν είναι συνεχής σε ένα εσωτερικό σημείο
𝑥0 ενός διαστήματος του πεδίου ορισμού της, τότε η 𝑓 δεν είναι
παραγωγίσιμη στο 𝑥0.
r Σ
r Λ
9. Αν οι συναρτήσεις 𝑓 και 𝑔 είναι παραγωγίσιμες στο 𝑥0 και
𝑔(𝑥0) ≠ 0, τότε και η συνάρτηση
𝑓
𝑔
είναι παραγωγίσιμη στο 𝑥0
και ισχύει:
𝑓
𝑔
′
(𝑥0) =
𝑓′(𝑥0)𝑔(𝑥0) − 𝑓(𝑥0)𝑔′(𝑥0)
[𝑔(𝑥0)]2
r Σ
r Λ
2o ΓΕΛ Καματερού 25 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 26 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-26-320.jpg)

![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2006: επαναληπτικές ημερήσια & εσπερινά + ομογενείς
Ερωτήσεις Απαντήσεις
1. Αν οι συναρτήσεις 𝑓 και 𝑔 είναι παραγωγίσιμες στο 𝑥0 και
𝑔(𝑥0) ≠ 0, τότε η συνάρτηση
𝑓
𝑔
είναι παραγωγίσιμη στο 𝑥0 και
ισχύει:
𝑓
𝑔
′
(𝑥0) =
𝑓(𝑥0)𝑔′(𝑥0) − 𝑓′(𝑥0)𝑔(𝑥0)
[𝑔(𝑥0)]2
r Σ
r Λ
2. Για κάθε 𝑥 ≠ 0 ισχύει [ln|𝑥|]
′
=
1
𝑥
.
r Σ
r Λ
3. Μια συνάρτηση 𝑓 ∶ 𝐴 → ℝ είναι 1 − 1, αν και μόνο αν για
κάθε στοιχείο 𝑦 του συνόλου τιμών της η εξίσωση 𝑦 = 𝑓(𝑥) έχει
ακριβώς μία λύση ως προς 𝑥.
r Σ
r Λ
4. Έστω η συνάρτηση 𝑓(𝑥) = εφ𝑥. Η συνάρτηση 𝑓 είναι
παραγωγίσιμη στο ℝ1 = ℝ − { 𝑥| συν𝑥 = 0 } και ισχύει
𝑓′(𝑥) = −
1
συν2 𝑥
r Σ
r Λ
5. Αν lim
𝑥→𝑥0
𝑓(𝑥) < 0, τότε 𝑓(𝑥) < 0 κοντά στο 𝑥0. r Σ
r Λ
2005: ημερήσια & εσπερινά
Ερωτήσεις Απαντήσεις
1. Αν η 𝑓 είναι συνεχής στο [𝛼, 𝛽] με 𝑓(𝛼) < 0 και υπάρχει
𝜉 ∈ (𝛼, 𝛽) ώστε 𝑓(𝜉) = 0, τότε κατ΄ ανάγκη 𝑓(𝛽) > 0.
r Σ
r Λ
2. Αν υπάρχει το lim
𝑥→𝑥0
𝑓(𝑥) + 𝑔(𝑥), τότε κατ΄ ανάγκη υπάρχουν
τα lim
𝑥→𝑥0
𝑓(𝑥) και lim
𝑥→𝑥0
𝑔(𝑥).
r Σ
r Λ
2o ΓΕΛ Καματερού 27 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 28 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-28-320.jpg)
![Μαθηματικά Προσανατολισμού Απρίλιος 2021
3. Αν η 𝑓 έχει αντίστροφη συνάρτηση 𝑓−1 και η γραφική
παράσταση της 𝑓 έχει κοινό σημείο Α με την ευθεία 𝑦 = 𝑥, τότε
το σημείο Α ανήκει και στη γραφική παράσταση της 𝑓−1.
r Σ
r Λ
4. Αν lim
𝑥→𝑥0
𝑓(𝑥) = 0 και 𝑓(𝑥) > 0 κοντά στο 𝑥0, τότε
lim
𝑥→𝑥0
1
𝑓(𝑥)
= +∞.
r Σ
r Λ
5. Αν μια συνάρτηση 𝑓 είναι συνεχής σε ένα διάστημα Δ και δε
μηδενίζεται σε αυτό, τότε αυτή ή είναι θετική για κάθε 𝑥 ∈ Δ ή
είναι αρνητική για κάθε 𝑥 ∈ Δ, δηλαδή διατηρεί πρόσημο στο
διάστημα Δ.
r Σ
r Λ
6. Μία συνάρτηση 𝑓 ∶ 𝐴 → ℝ λέγεται συνάρτηση 1 − 1, όταν
για οποιαδήποτε 𝑥1, 𝑥2 ∈ 𝐴 ισχύει η συνεπαγωγή:
αν 𝑥1 ≠ 𝑥2, τότε 𝑓(𝑥1) ≠ 𝑓(𝑥2).
r Σ
r Λ
7. Μία συνάρτηση 𝑓 με πεδίο ορισμού Α θα λέμε ότι
παρουσιάζει στο 𝑥0 ∈ Α (ολικό) ελάχιστο, το 𝑓(𝑥0), όταν
𝑓(𝑥) < 𝑓(𝑥0) για κάθε 𝑥 ∈ 𝐴.
r Σ
r Λ
8. Αν οι συναρτήσεις 𝑓, 𝑔 έχουν όριο στο 𝑥0 και ισχύει
𝑓(𝑥) ≤ 𝑔(𝑥) κοντά στο 𝑥0, τότε lim
𝑥→𝑥0
𝑓(𝑥) > lim
𝑥→𝑥0
𝑔(𝑥).
r Σ
r Λ
9. Αν μία συνάρτηση 𝑓 είναι συνεχής στο κλειστό διάστημα
[𝛼, 𝛽] και παραγωγίσιμη στο ανοικτό διάστημα (𝛼, 𝛽) τότε
υπάρχει ένα, τουλάχιστον, 𝜉 ∈ (𝛼, 𝛽) τέτοιο, ώστε:
𝑓′(𝜉) =
𝑓(𝛽) − 𝑓(𝛼)
𝛽 − 𝛼
.
r Σ
r Λ
2o ΓΕΛ Καματερού 28 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 29 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-29-320.jpg)
![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2005: επαναληπτικές ημερήσια & εσπερινά + ομογενείς
Ερωτήσεις Απαντήσεις
1. Τα εσωτερικά σημεία του διαστήματος Δ, στα οποία η 𝑓 δεν
παραγωγίζεται ή η παράγωγός της είναι ίση με το 0, λέγονται
κρίσιμα σημεία της 𝑓 στο διάστημα Δ.
r Σ
r Λ
2. Έστω μία συνάρτηση 𝑓 παραγωγίσιμη σε ένα διάστημα (𝛼, 𝛽) με
εξαίρεση ίσως ένα σημείο του 𝑥0. Αν η 𝑓 είναι κυρτή στο (𝛼, 𝑥0) και
κοίλη στο (𝑥0, 𝛽) ή αντιστρόφως, τότε το σημείο 𝐴(𝑥0, 𝑓(𝑥0)) είναι
υποχρεωτικά σημείο καμπής της γραφικής παράστασης της 𝑓.
r Σ
r Λ
3. Αν για δύο συναρτήσεις 𝑓, 𝑔 ορίζονται οι 𝑓 ∘ 𝑔 και 𝑔 ∘ 𝑓, τότε
είναι υποχρεωτικά 𝑓 ∘ 𝑔 ≠ 𝑔 ∘ 𝑓.
r Σ
r Λ
4. Αν 𝑥 ≠ 0, τότε ισχύει lim
𝑥→0
1
𝑥2
= −∞. r Σ
r Λ
5. Έστω η συνάρτηση 𝑓(𝑥) = εφ𝑥. Η συνάρτηση 𝑓 είναι
παραγωγίσιμη στο ℝ1 = ℝ − { 𝑥| συν𝑥 = 0 } και ισχύει:
𝑓′(𝑥) =
1
συν2 𝑥
.
r Σ
r Λ
6. Αν υπάρχει το όριο της συνάρτησης 𝑓 στο 𝑥0 ∈ ℝ, τότε:
lim
𝑥→𝑥0
𝑘𝑓(𝑥) = 𝑘 ⋅ lim
𝑥→𝑥0
(𝑓(𝑥)), για κάθε σταθερά 𝑘 ∈ ℝ.
r Σ
r Λ
7. Αν υπάρχει το όριο της συνάρτησης 𝑓 στο 𝑥0, τότε ισχύει
lim
𝑥→𝑥0
|𝑓(𝑥)| = | lim
𝑥→𝑥0
𝑓(𝑥)|.
r Σ
r Λ
8. Ισχύει (ημ𝑥)′ = − συν𝑥. r Σ
r Λ
9. Αν 𝑓 είναι συνεχής συνάρτηση στο [𝛼, 𝛽], τότε η 𝑓 παίρνει
στο [𝛼, 𝛽] μια μέγιστη τιμή 𝑀 και μια ελάχιστη τιμή 𝑚.
r Σ
r Λ
2o ΓΕΛ Καματερού 29 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 30 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-30-320.jpg)



![Μαθηματικά Προσανατολισμού Απρίλιος 2021
2003: επαναληπτικές ημερήσια & εσπερινά + ομογενείς
Ερωτήσεις Απαντήσεις
1. Έστω μία συνάρτηση 𝑓 παραγωγίσιμη σε ένα διάστημα (𝛼, 𝛽),
με εξαίρεση ίσως ένα σημείο του 𝑥0, στο οποίο όμως η 𝑓 είναι
συνεχής. Αν 𝑓′(𝑥) > 0 στο (𝛼, 𝑥0) και 𝑓′(𝑥) < 0 στο (𝑥0, 𝛽), τότε το
𝑓(𝑥0) είναι τοπικό ελάχιστο της 𝑓.
r Σ
r Λ
2. Μία συνάρτηση 𝑓∶ 𝐴 → ℝ είναι συνάρτηση 1 − 1, αν και μόνο
αν για οποιαδήποτε 𝑥1, 𝑥2 ∈ 𝐴 ισχύει η συνεπαγωγή:
αν 𝑥1 = 𝑥2, τότε 𝑓(𝑥1) = 𝑓(𝑥2)
r Σ
r Λ
2002: ημερήσια & εσπερινά
Ερωτήσεις Απαντήσεις
1. Αν η συνάρτηση 𝑓 είναι ορισμένη στο [𝛼, 𝛽] και συνεχής στο
(𝛼, 𝛽], τότε η 𝑓 παίρνει πάντοτε στο [𝛼, 𝛽] μία μέγιστη τιμή.
r Σ
r Λ
2. Κάθε συνάρτηση, που είναι 1 − 1 στο πεδίο ορισμού της, είναι
γνησίως μονότονη
r Σ
r Λ
3. Αν υπάρχει το όριο της συνάρτησης 𝑓 στο 𝑥0 και
lim
𝑥→𝑥0
|𝑓(𝑥)| = 0, τότε lim
𝑥→𝑥0
𝑓(𝑥) = 0
r Σ
r Λ
4. Αν lim
𝑥→𝑥0
𝑓(𝑥) > 0, τότε 𝑓(𝑥) > 0 κοντά στο 𝑥0. r Σ
r Λ
5. Αν μία συνάρτηση 𝑓 είναι παραγωγίσιμη σε ένα σημείο 𝑥0, τότε
είναι και συνεχής στο σημείο αυτό.
r Σ
r Λ
6. Αν μία συνάρτηση 𝑓 είναι συνεχής σε ένα σημείο 𝑥0, τότε είναι
και παραγωγίσιμη στο σημείο αυτό.
r Σ
r Λ
7. Αν μία συνάρτηση 𝑓 είναι συνεχής σε ένα διάστημα Δ και ισχύει
𝑓′(𝑥) = 0 σε κάθε εσωτερικό σημείο 𝑥 του Δ, τότε η 𝑓 είναι
γνησίως φθίνουσα στο Δ.
r Σ
r Λ
2o ΓΕΛ Καματερού 33 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 34 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-34-320.jpg)
![Μαθηματικά Προσανατολισμού Απρίλιος 2021
8. Αν μία συνάρτηση 𝑓 είναι συνεχής σε ένα διάστημα Δ και ισχύει
𝑓′(𝑥) > 0 σε κάθε εσωτερικό σημείο 𝑥 του Δ, τότε η 𝑓 είναι
γνησίως αύξουσα στο Δ.
r Σ
r Λ
9. Αν υπάρχουν τα όρια των συναρτήσεων 𝑓 και 𝑔 στο 𝑥0, τότε
ισχύει:
lim
𝑥→𝑥)
𝑓(𝑥) + 𝑔(𝑥) = lim
𝑥→𝑥0
𝑓(𝑥) + lim
𝑥→𝑥0
𝑔(𝑥)
r Σ
r Λ
10. Αν υπάρχουν τα όρια των συναρτήσεων 𝑓 και 𝑔 στο 𝑥0, τότε
ισχύει:
lim
𝑥→𝑥)
𝑓(𝑥) ⋅ 𝑔(𝑥) = lim
𝑥→𝑥0
𝑓(𝑥) − lim
𝑥→𝑥0
𝑔(𝑥)
r Σ
r Λ
2002: επαναληπτικές ημερήσια & εσπερινά
Ερωτήσεις Απαντήσεις
1. Η εικόνα 𝑓(Δ) ενός διαστήματος Δ μέσω μιας συνεχούς και μη
σταθερής συνάρτησης 𝑓 είναι διάστημα.
r Σ
r Λ
2. Αν η συνάρτηση 𝑓 είναι παραγωγίσιμη στο ℝ και δεν είναι
αντιστρέψιμη, τότε υπάρχει κλειστό διάστημα [𝛼, 𝛽], στο οποίο η
𝑓 ικανοποιεί τις προϋποθέσεις του θεωρήματος Rolle.
r Σ
r Λ
3. Έστω συνάρτηση 𝑓 ορισμένη και παραγωγίσιμη στο διάστημα
[𝛼, 𝛽] και σημείο 𝑥0 ∈ [𝛼, 𝛽] στο οποίο η 𝑓 παρουσιάζει τοπικό
μέγιστο. Τότε πάντα ισχύει ότι 𝑓′(𝑥0) = 0.
r Σ
r Λ
4. Αν η συνάρτηση 𝑓 είναι συνεχής στο διάστημα [𝛼, 𝛽] και
υπάρχει 𝑥0 ∈ (𝛼, 𝛽) τέτοιο ώστε 𝑓(𝑥0) = 0, τότε κατ΄ ανάγκη θα
ισχύει 𝑓(𝛼) ⋅ 𝑓(𝛽) < 0.
r Σ
r Λ
2o ΓΕΛ Καματερού 34 Κωνσταντίνος Γεωργίου
Μαθηματικός, MSc
27/4/21 Αποκλειστικά στο lisari.blogspot.com Page 35 of 38](https://image.slidesharecdn.com/tf2021teliko-210427151648/85/2021-35-320.jpg)