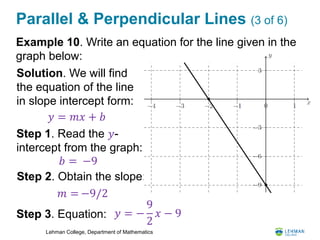
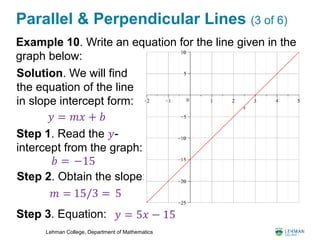
This document provides a lesson on linear relations and lines. It includes the following key points:
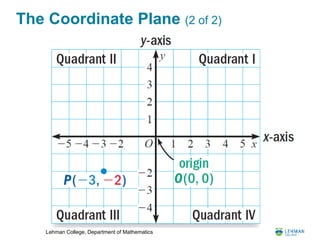
- It introduces the coordinate plane and how points are represented by ordered pairs.
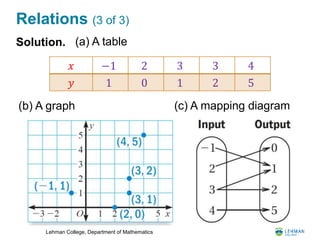
- It discusses relations and functions, including how to represent them using tables, graphs, and mapping diagrams. It also discusses the vertical line test for identifying functions.
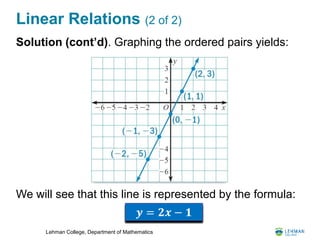
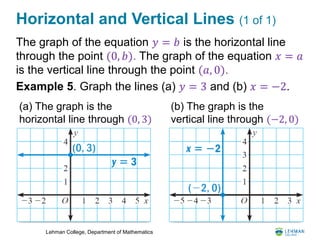
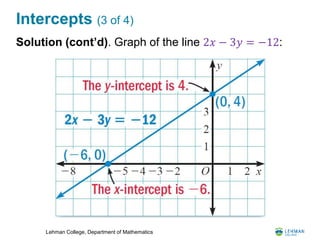
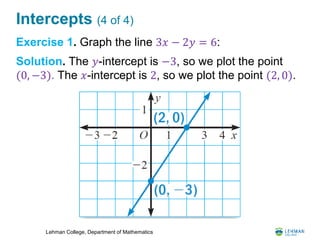
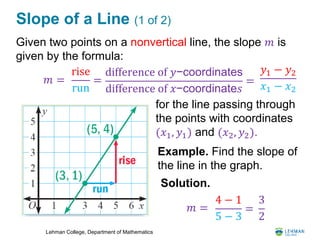
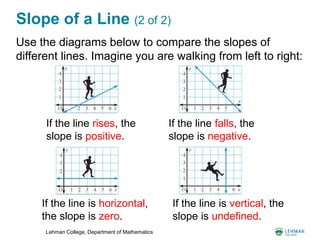
- It covers linear relations and how their graphs form straight lines. It shows how to find the slope and equation of a line.
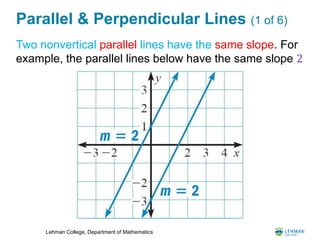
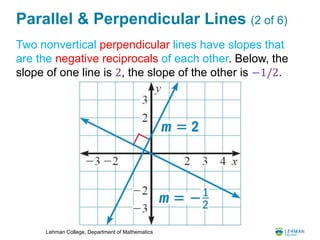
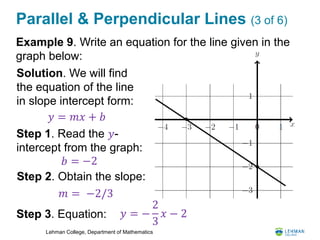
- It examines parallel and perpendicular lines, including how to find the equation of a line parallel or perpendicular to another given line.