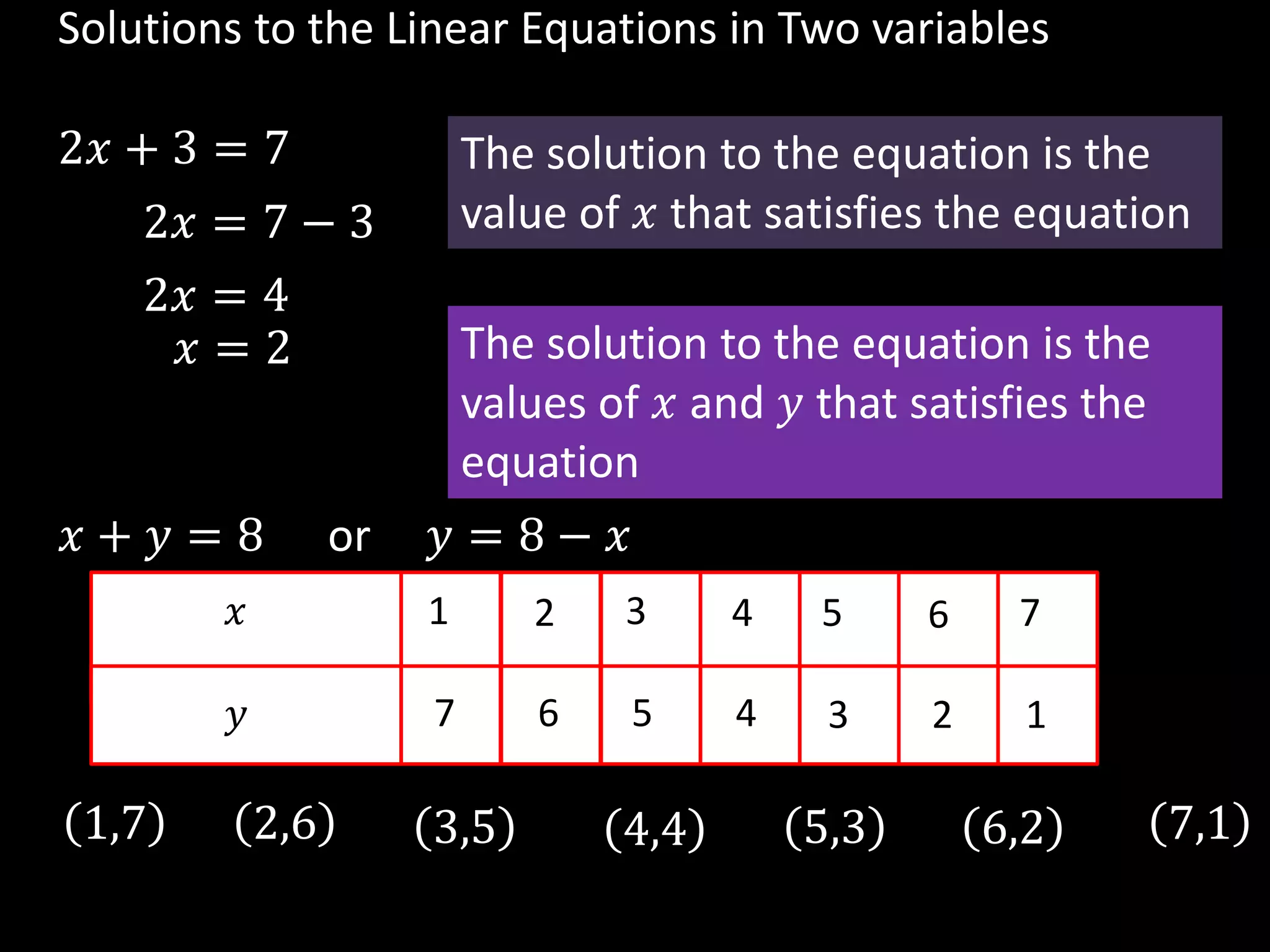
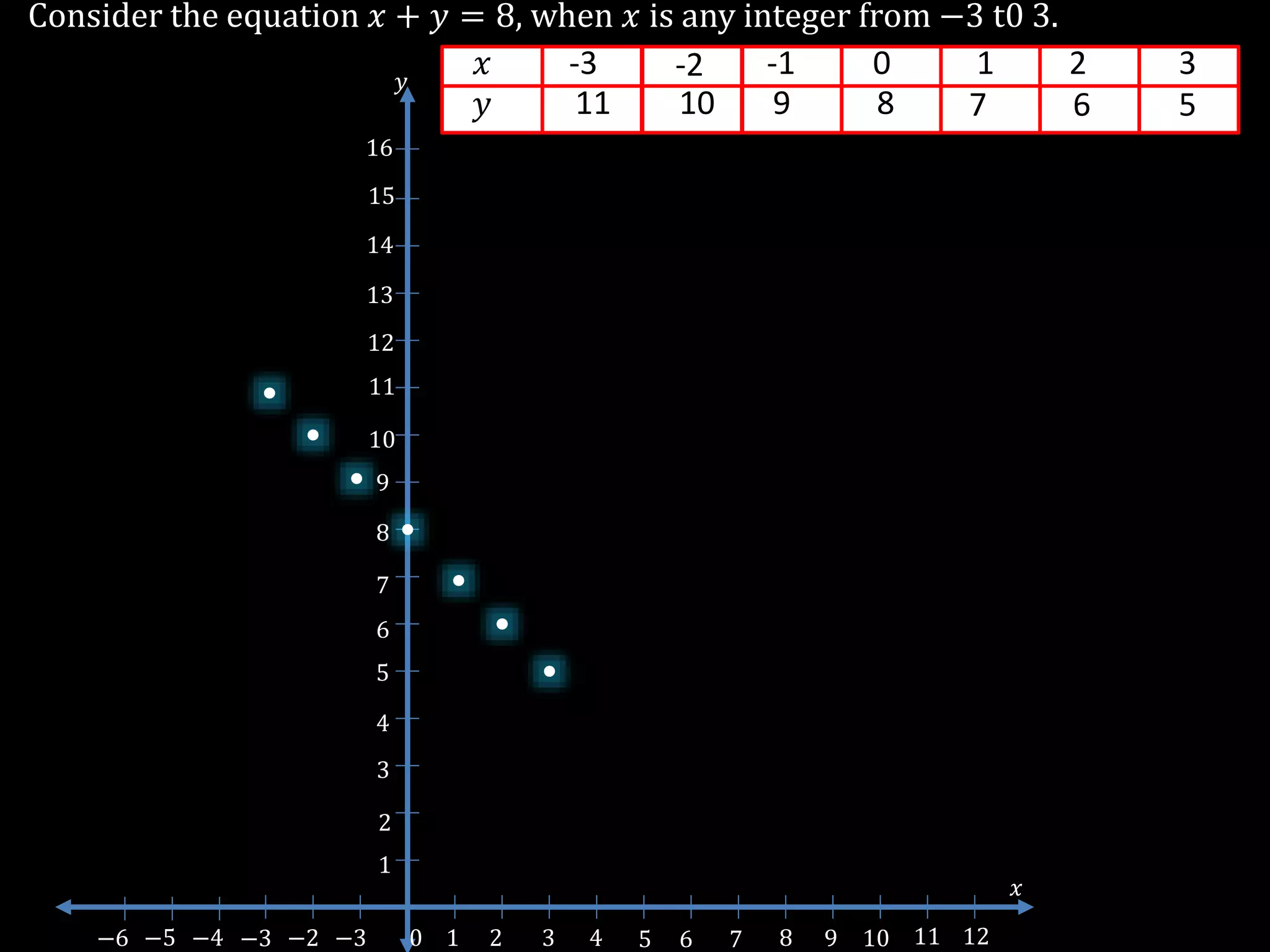
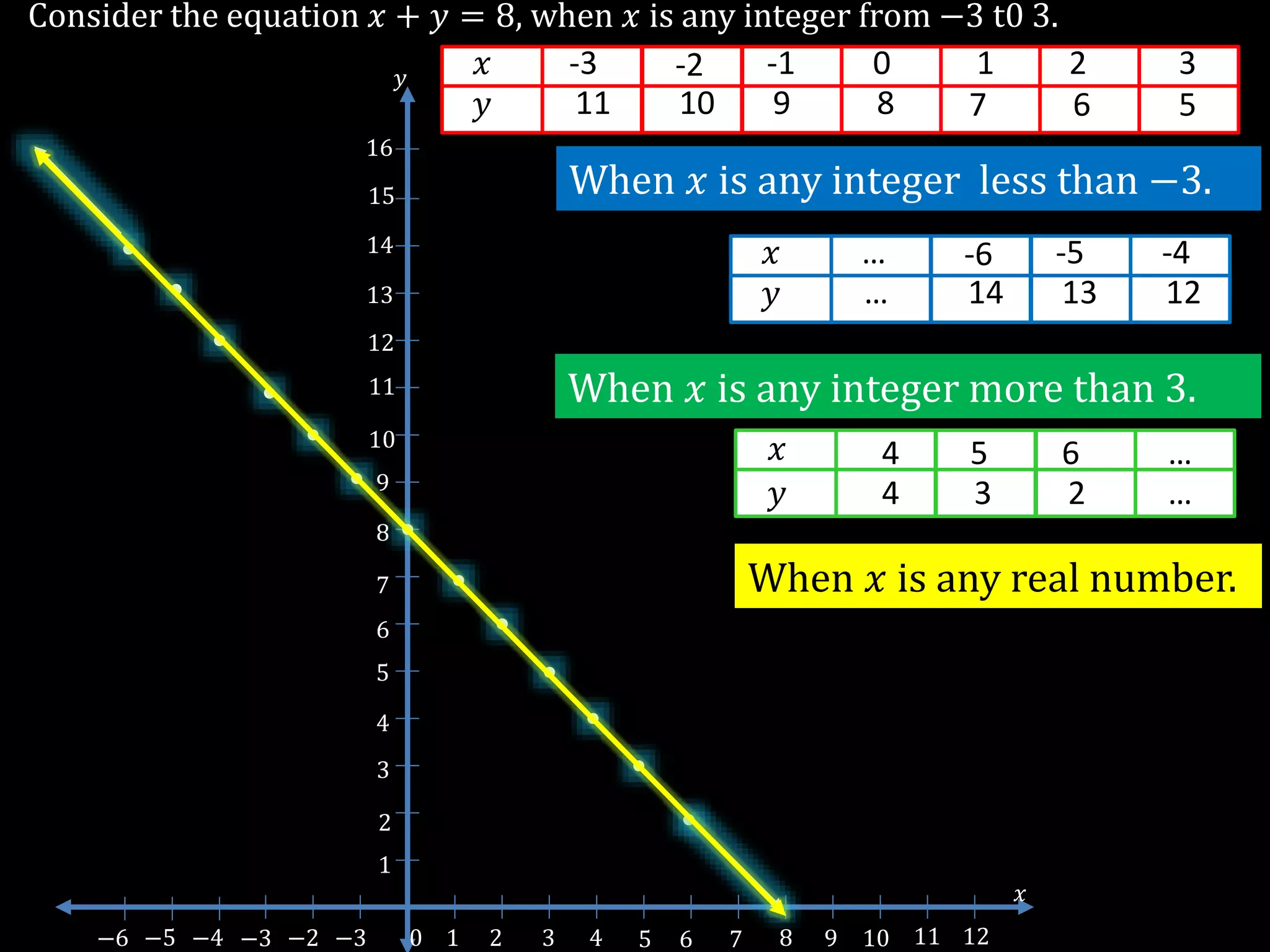
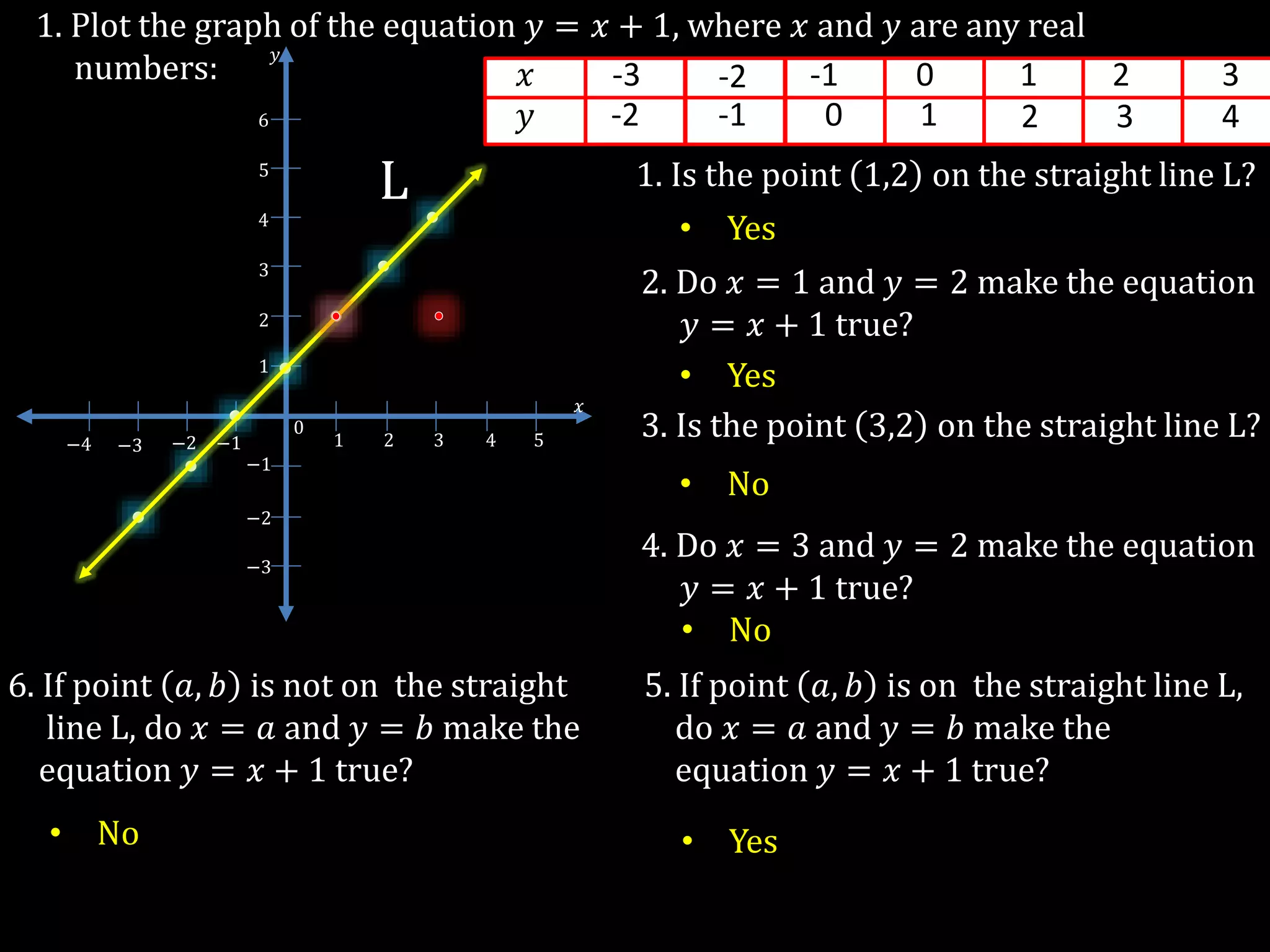
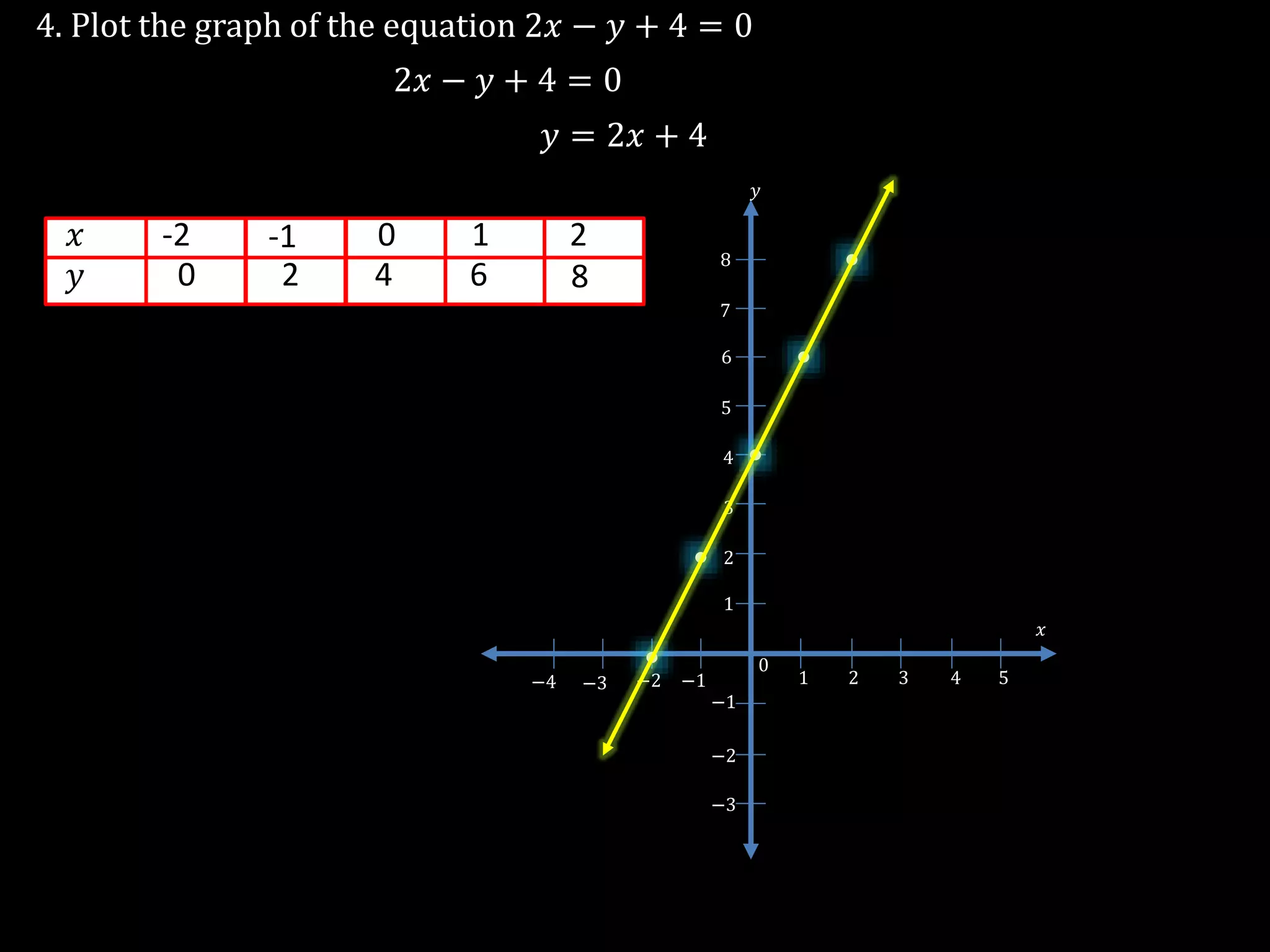
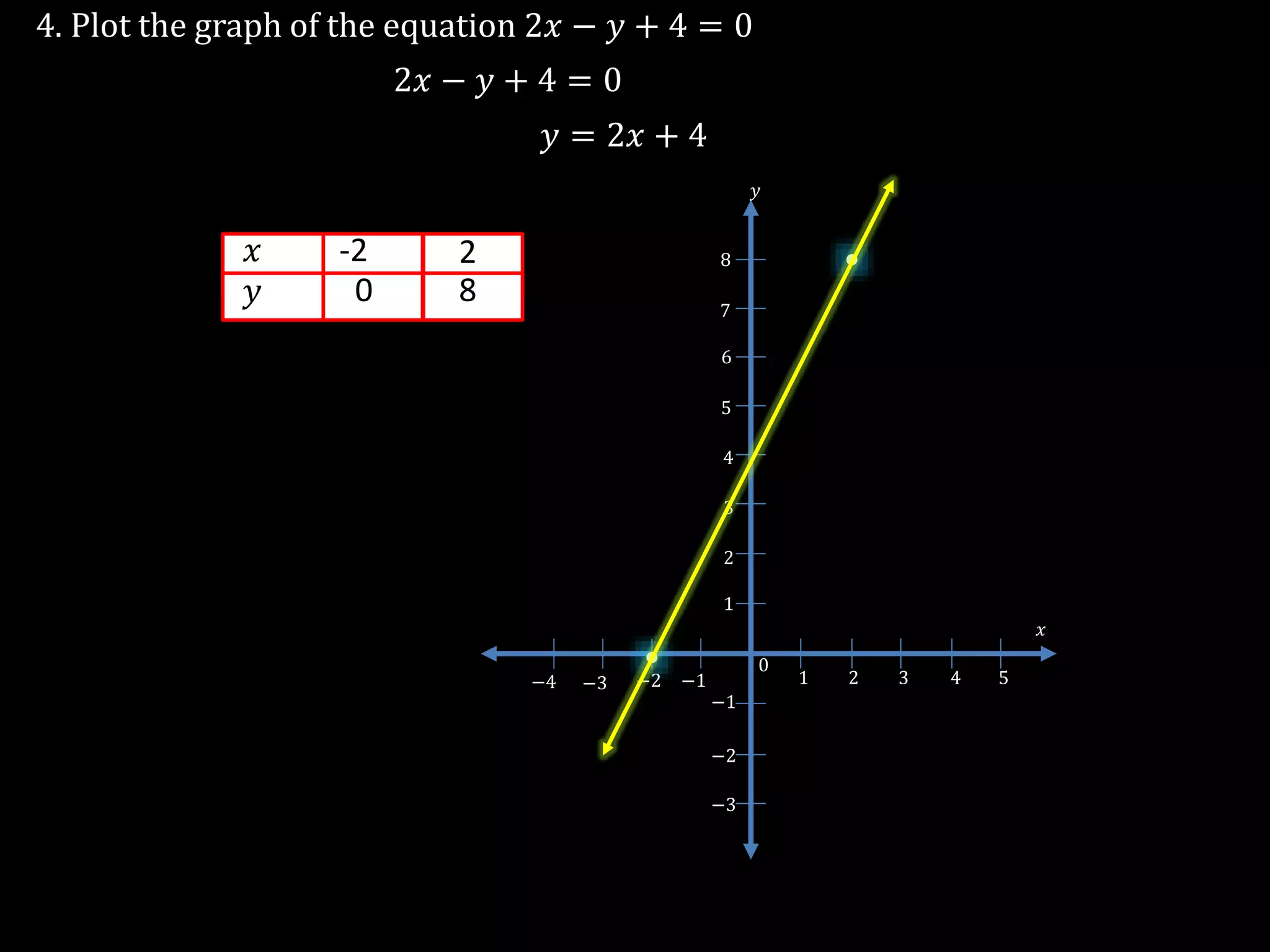
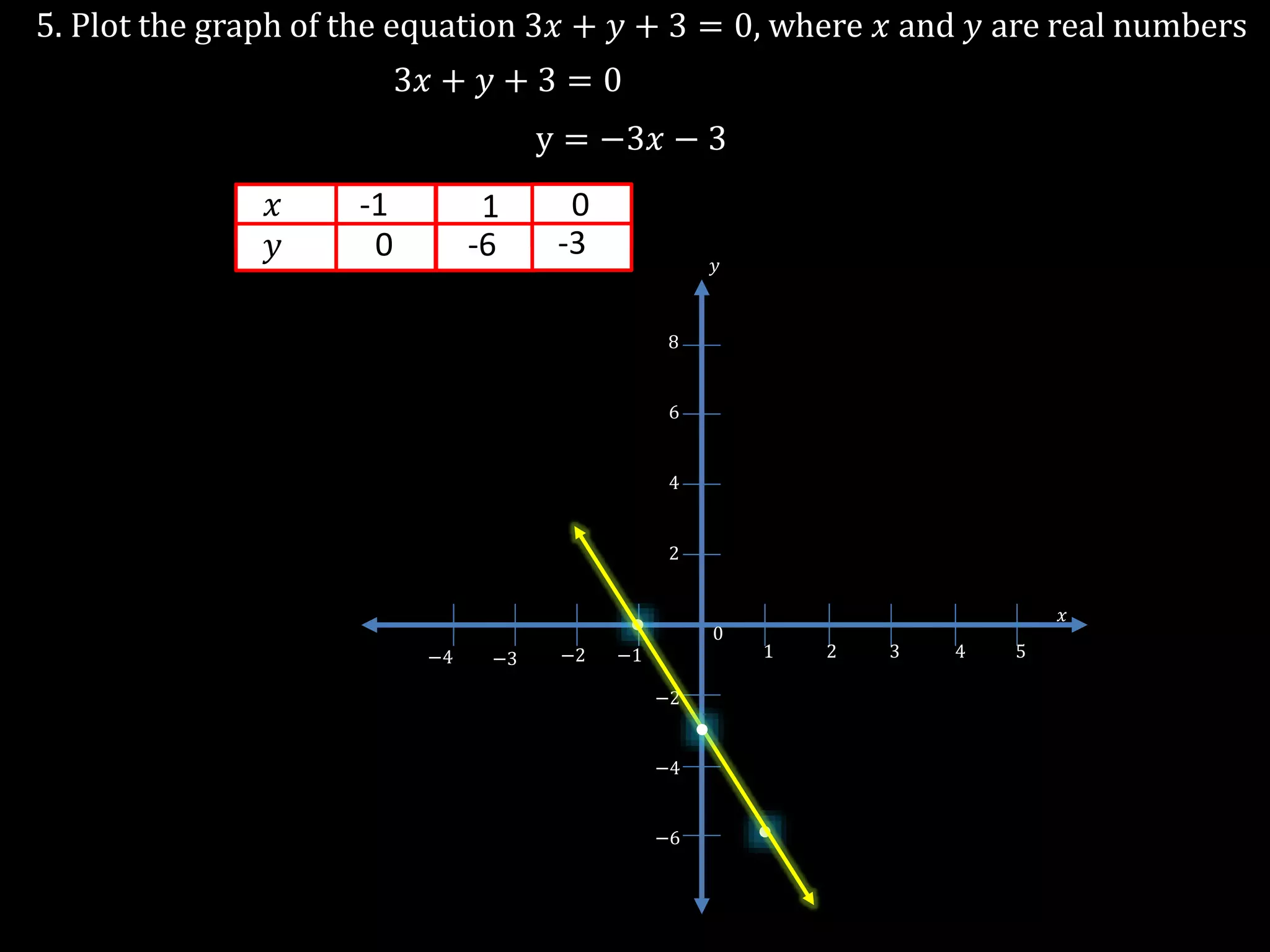
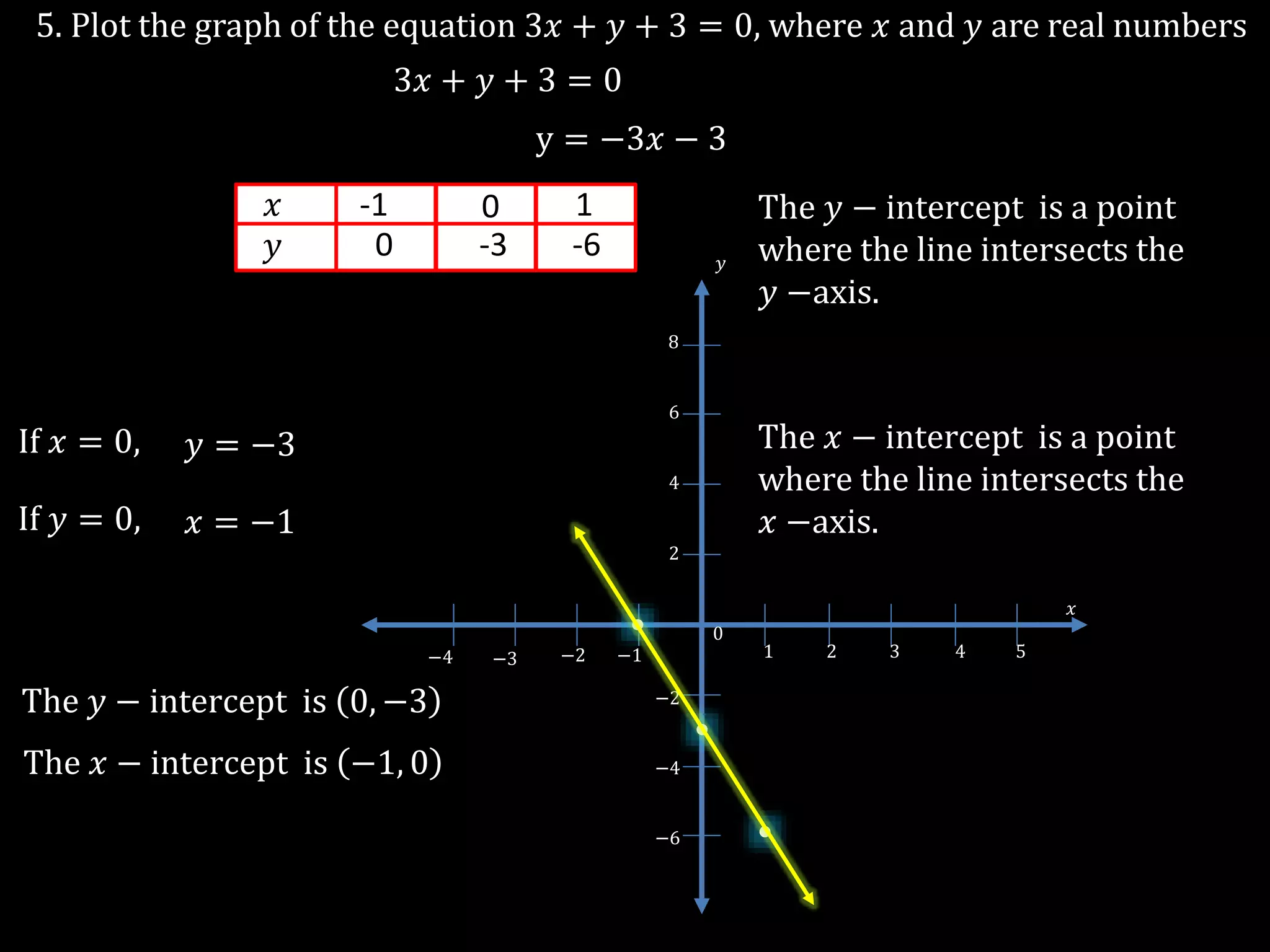
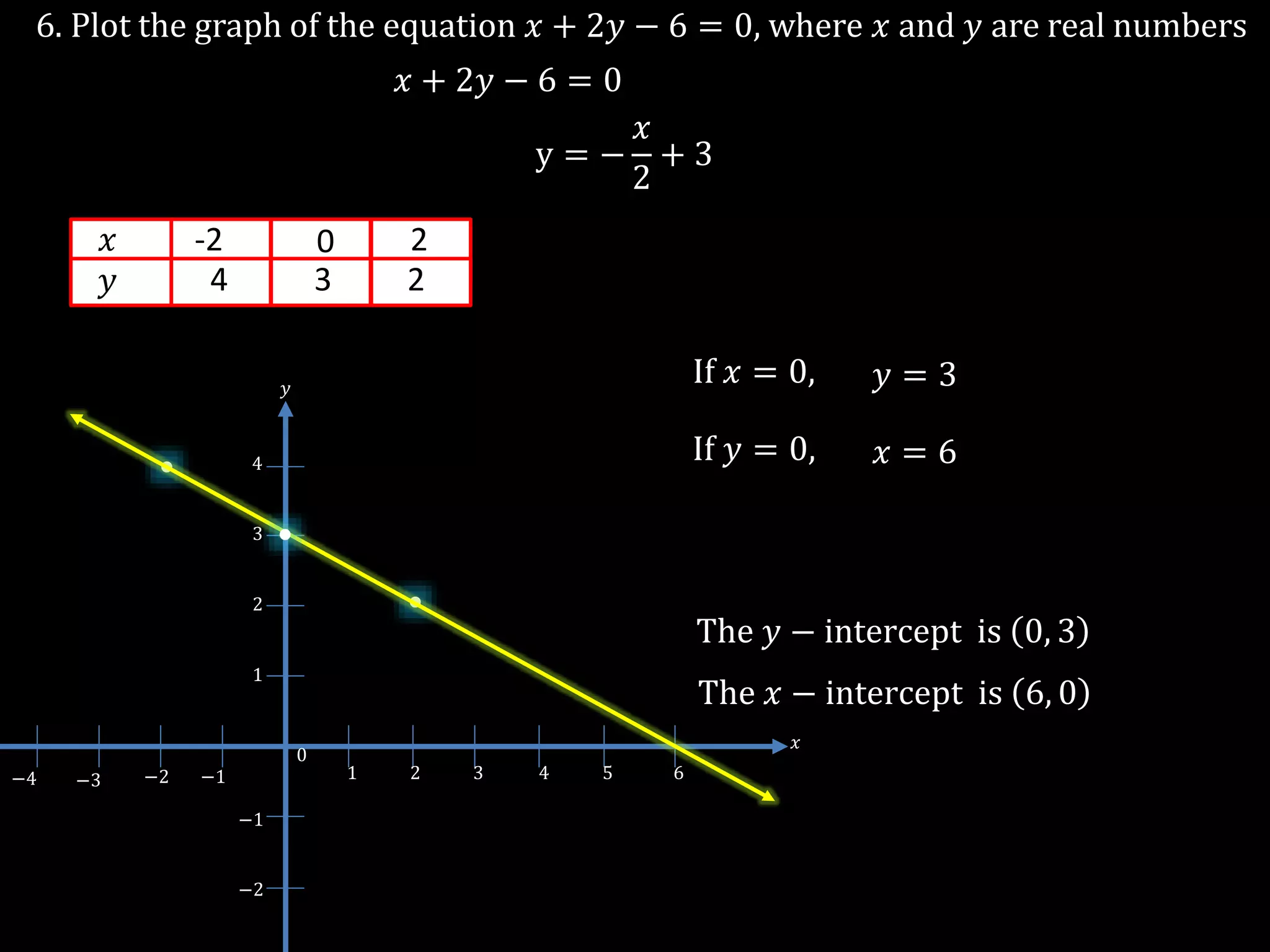
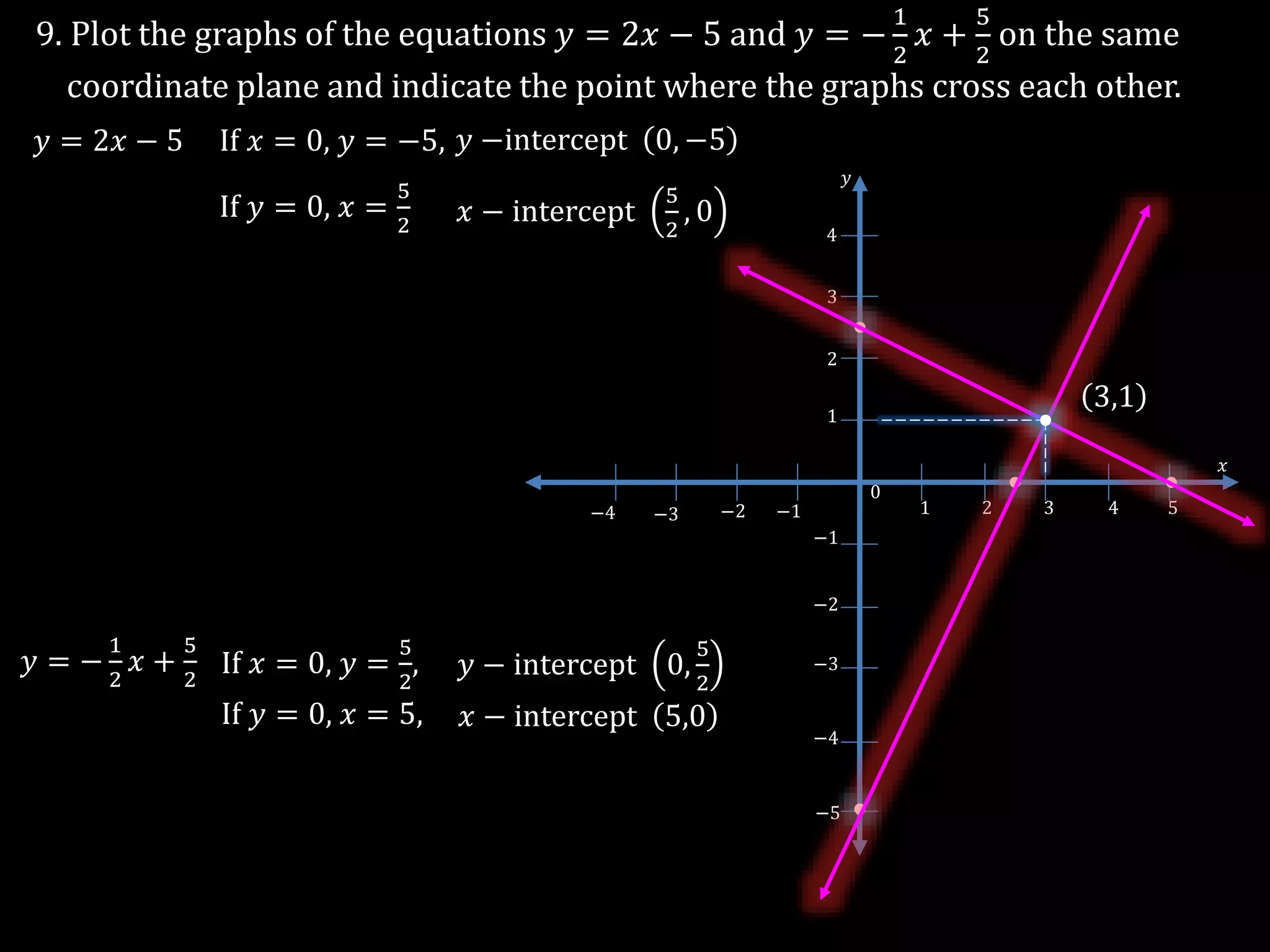
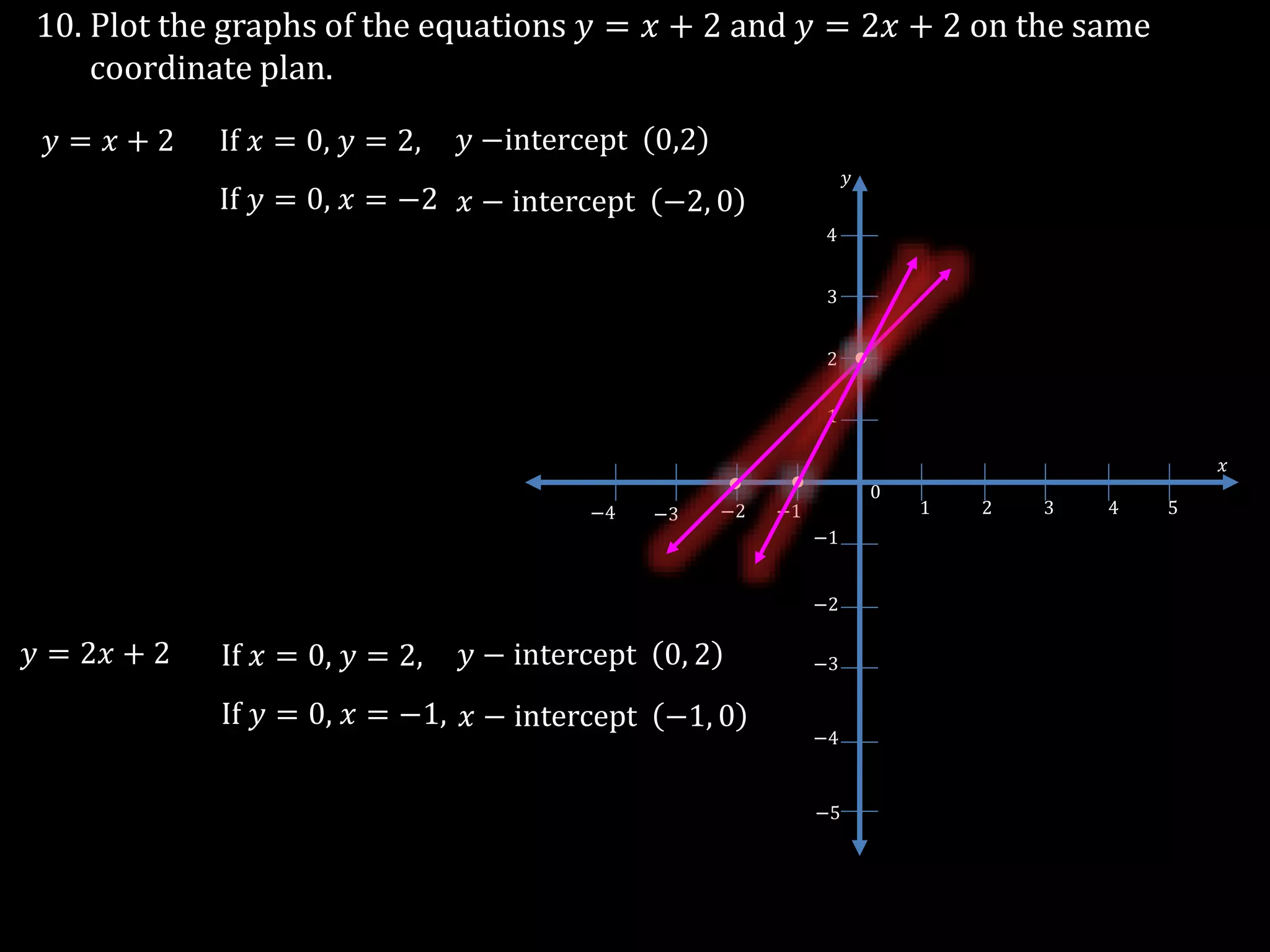
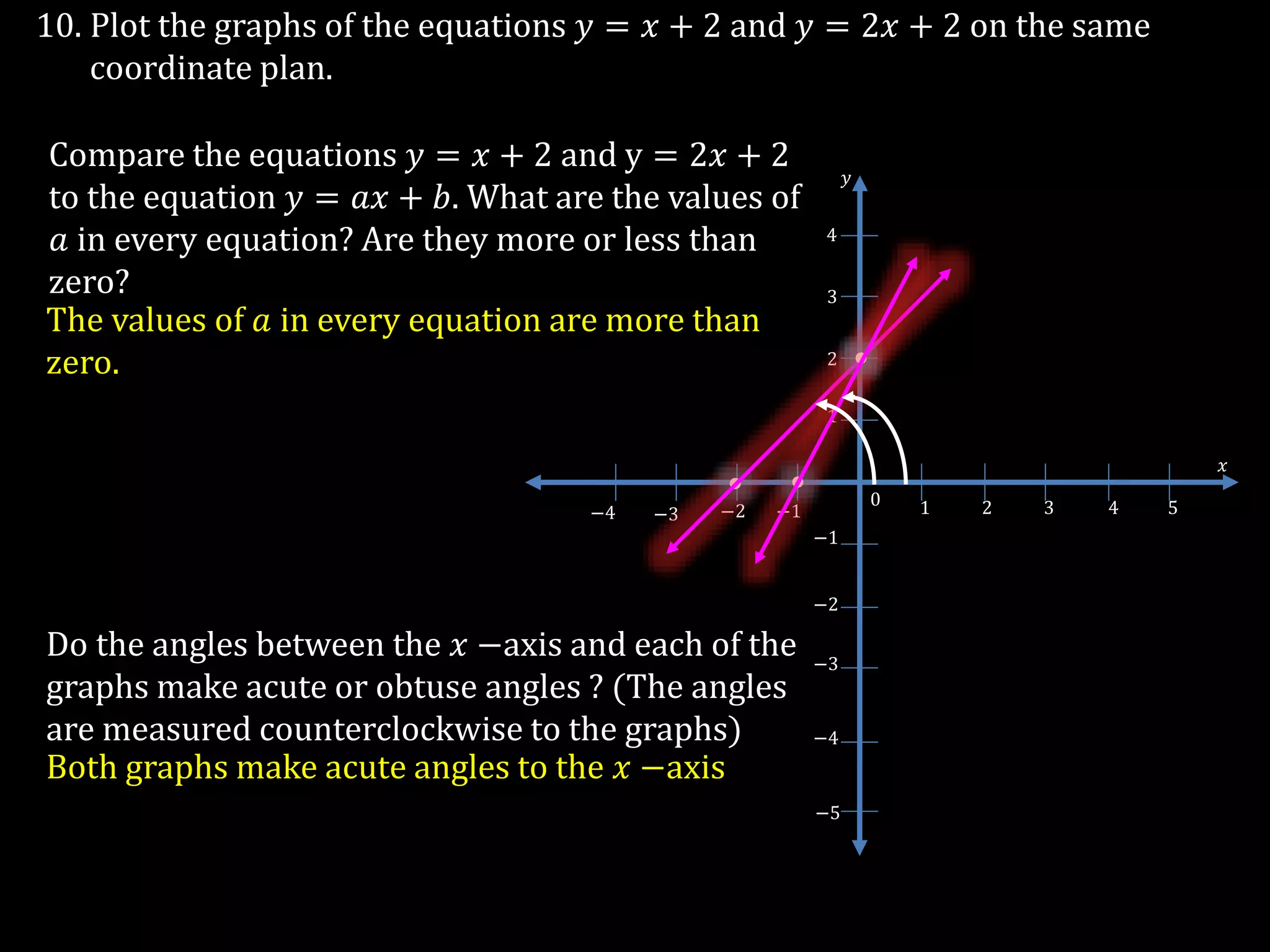
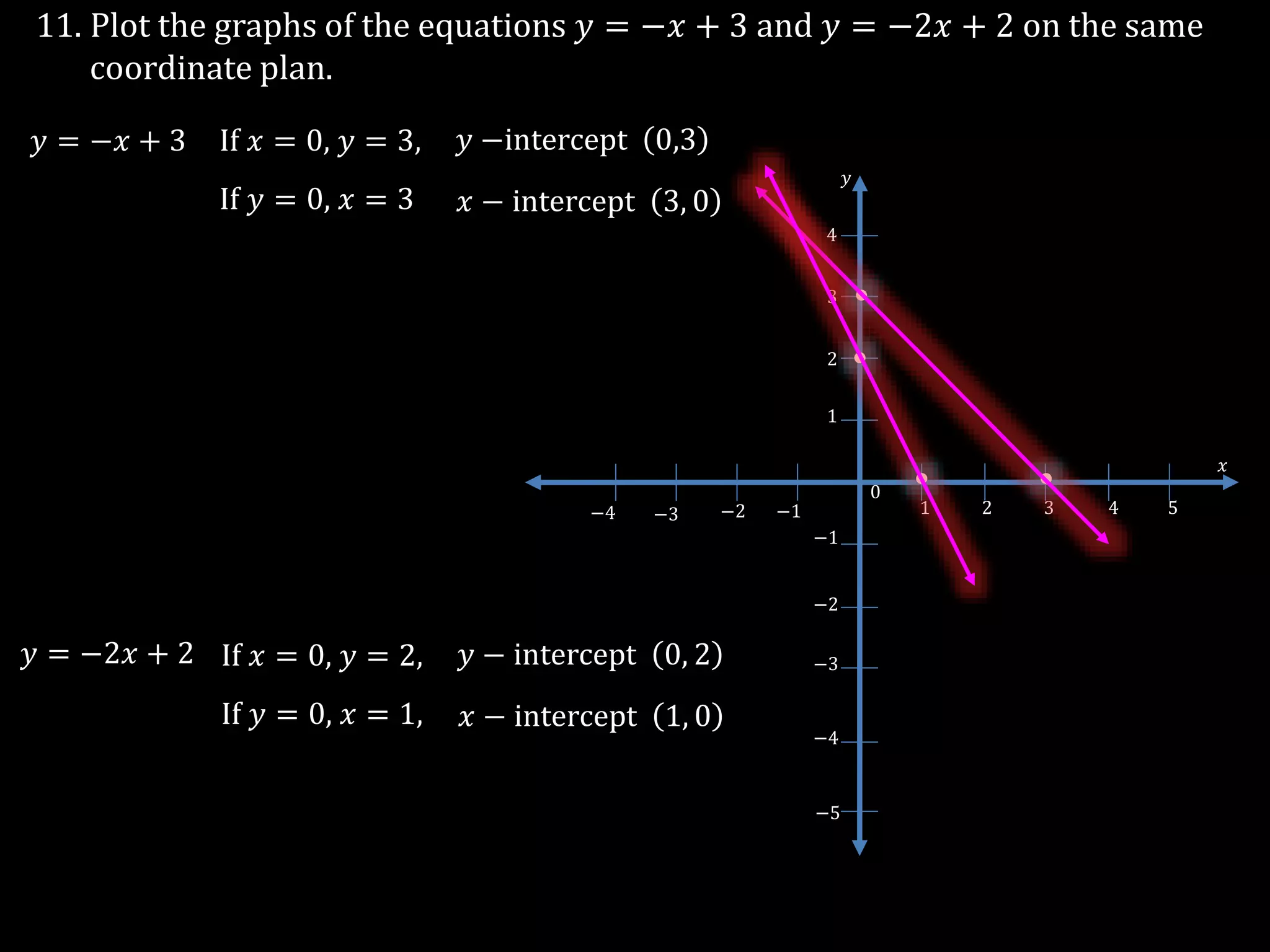
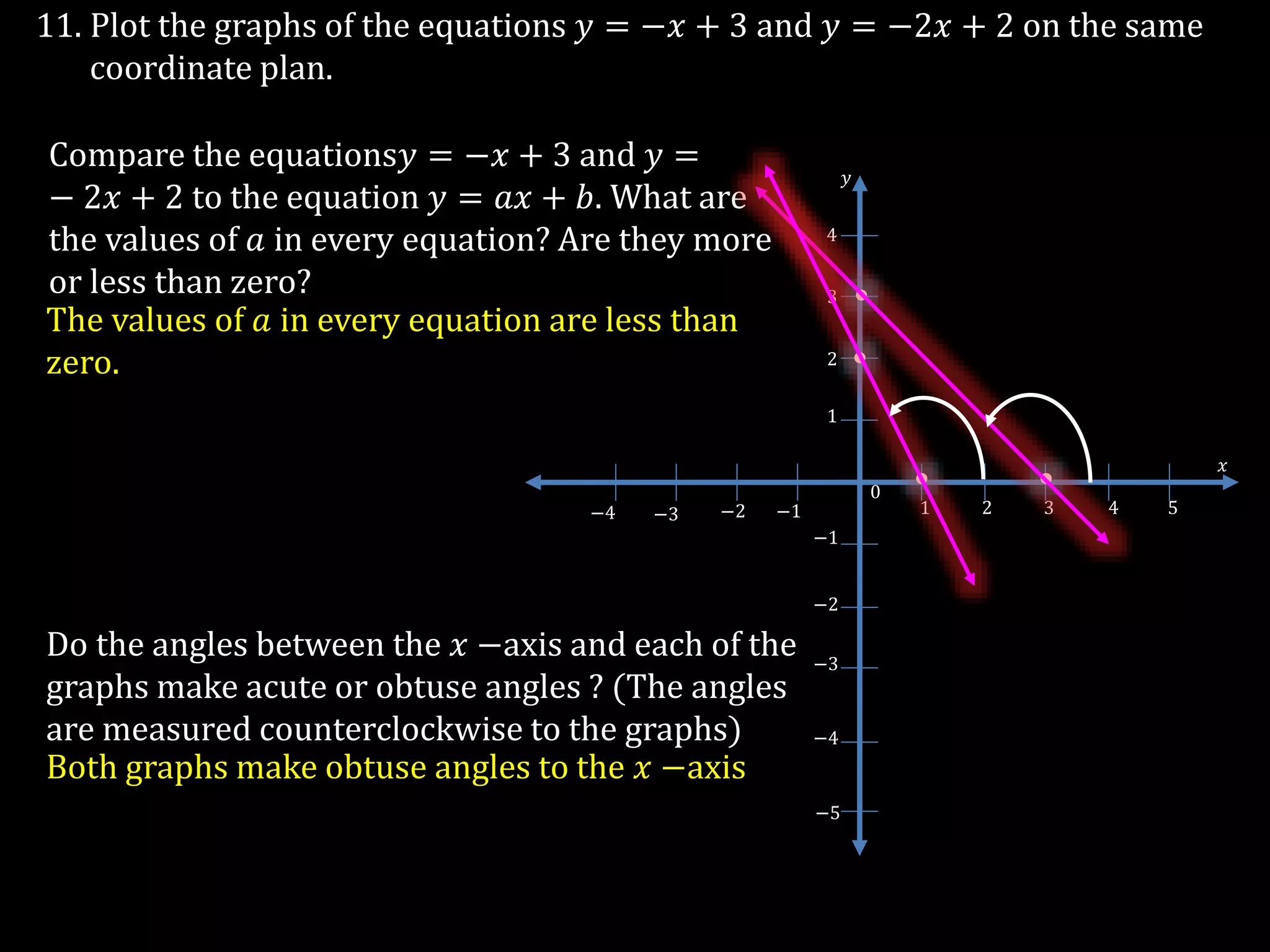
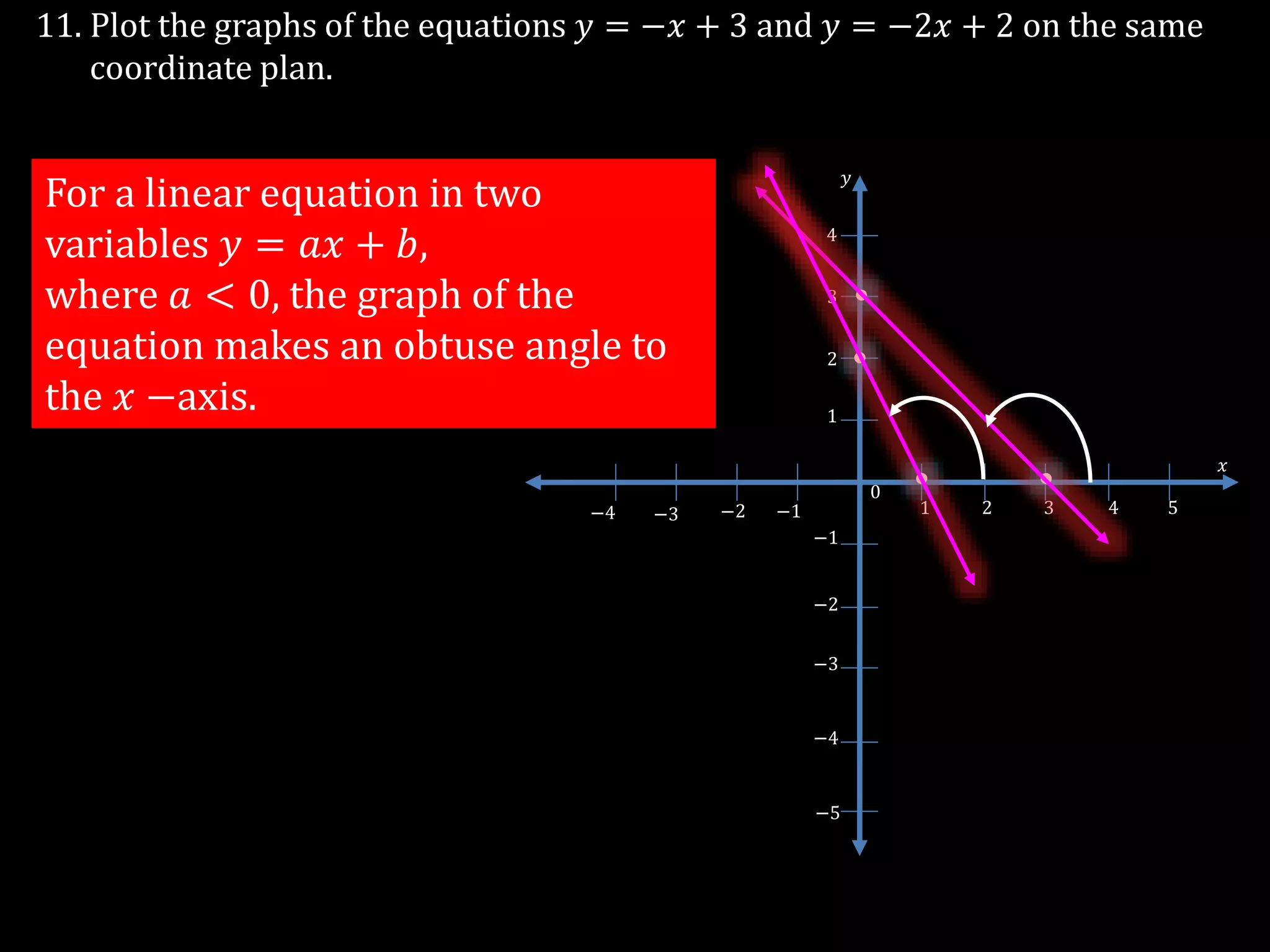
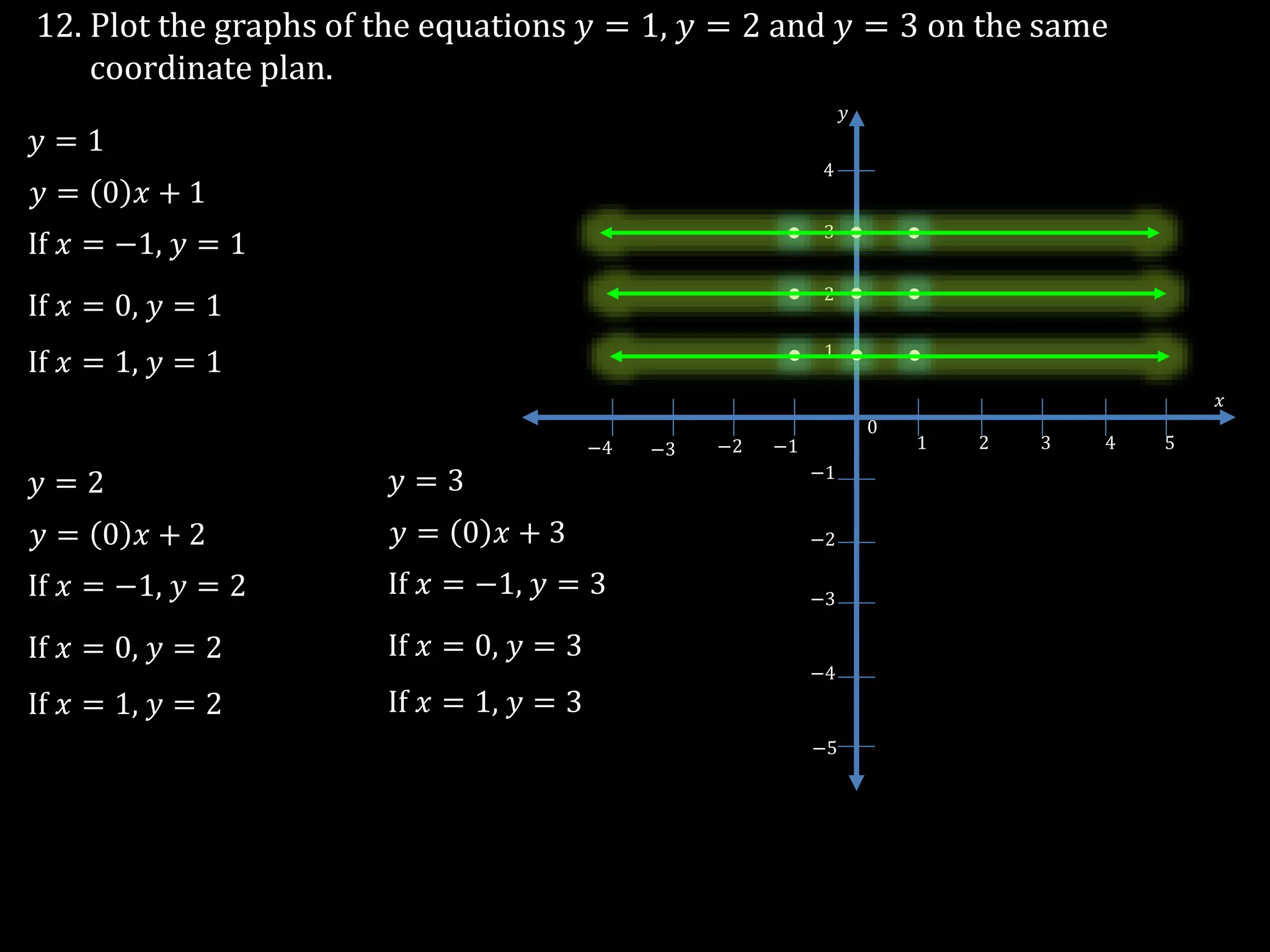
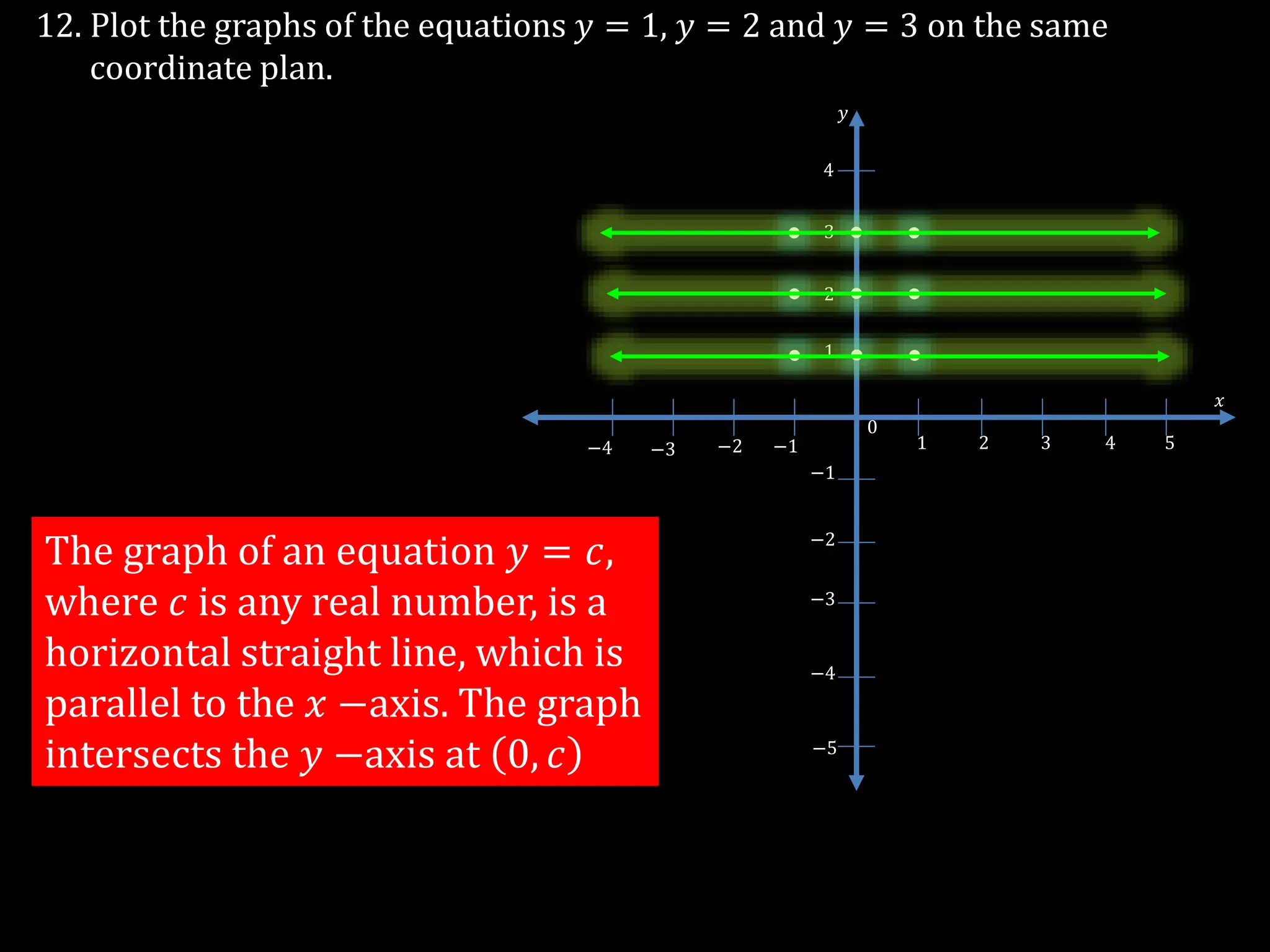
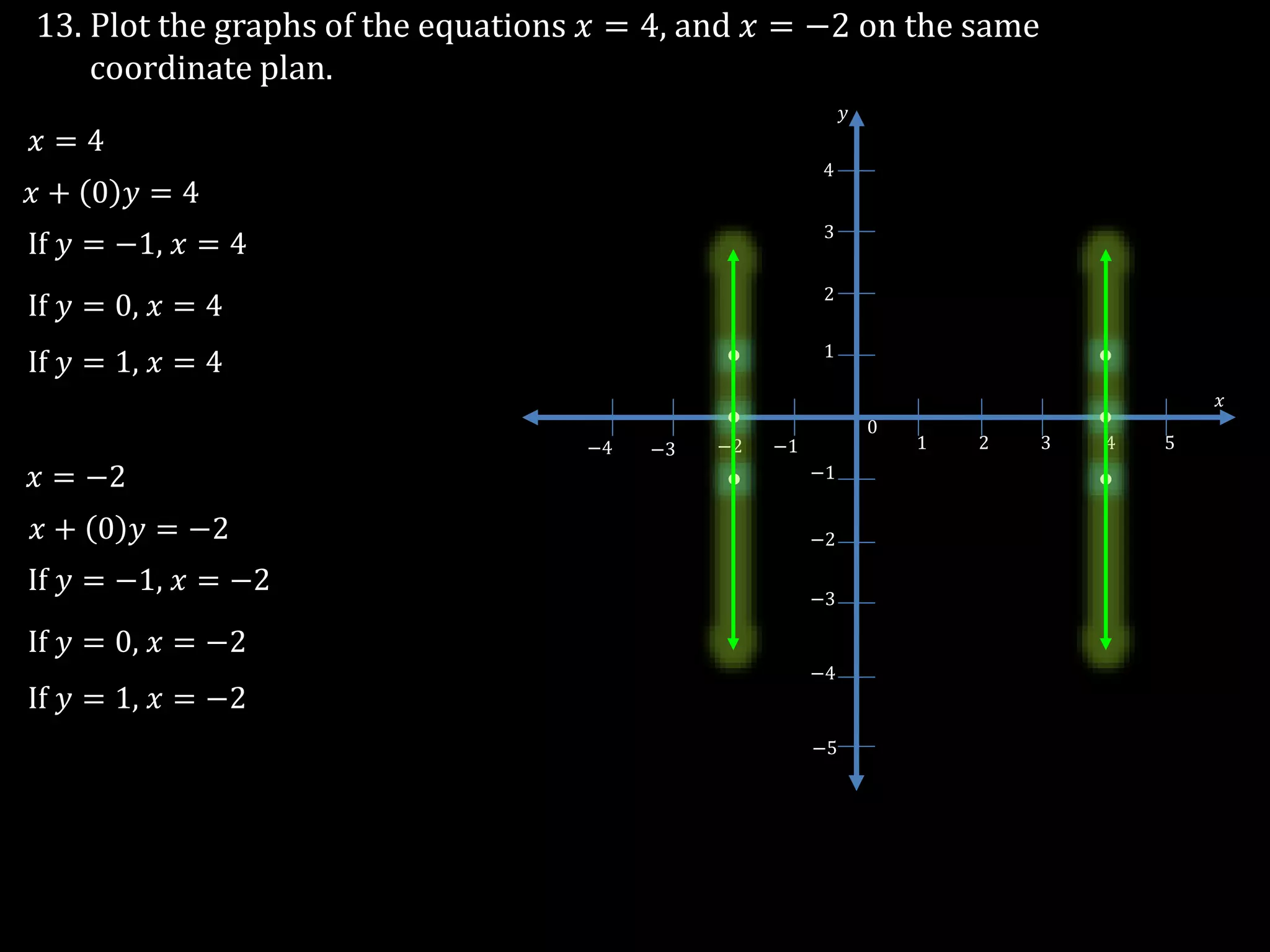
The document discusses linear equations in two variables, detailing their forms, properties, and the methods to find their solutions. It includes examples of rewriting sentences as equations, finding solutions to equations, and graphing these equations on a coordinate plane. Additionally, it provides examples of how to identify if specific points lie on the graphs of these equations.

1. LINEAR EQUATIONS
TWO
VARIABLES

2. The sum of twice a number and 3 is 7
2𝑥 + 3 = 7 Linear equation in
one variable
Only one variable (𝑥)
The sum of Got and Bas money is 30 baht.
𝑥 + 𝑦 = 30 or 𝑥 + 𝑦 − 30 = 0
The length of a rectangle is 2 units more than its width.
𝑦 = 𝑥 + 2 or 𝑦 − 𝑥 − 2 = 0

3. 𝑦 = 𝑥 + 2 and 𝑥 + 𝑦 = 30
have two variables: 𝑥 and 𝑦
You will notice that the exponents of 𝑥 and 𝑦 are 1
There is no product of 𝑥 and 𝑦 involved
Linear equation with Two Variables
2𝑥 − 8 = 0 3𝑦 − 7 = 0
2𝑥 + 0 𝑦 − 8 = 0 0 𝑥 + 3𝑦 − 7 = 0

4. An equation in the form of A𝑥 + 𝐵𝑦 + 𝐶 = 0,
where 𝐴, 𝐵, and 𝐶 are constants that 𝐴 and 𝐵 are not
simultaneously equal to zero, and 𝑥 and 𝑦 are variables is
called Linear Equations in Two Variables
Properties of Linear Equations in Two Variables
1. There are two variables
2. The exponent of each variable is 1
3. There is no multiplication of the variables

5. Are the following equations, where 𝑥 and 𝑦 are variables,
linear equations in two variables? If so, find the values of
A, B, and C written in the form of A𝑥 + 𝐵𝑦 + 𝐶 = 0
1. 3𝑥 + 2𝑦 − 1 = 0
2. 4𝑥 + 2𝑦 = −3
3. 2𝑥 + 𝑥𝑦 − 1 = 2
4. 𝑥 + 𝑦2 = 10
𝐴 = 3, 𝐵 = 2, 𝐶 = −1
𝐴 = 4, 𝐵 = 2, 𝐶 = 3
Not a linear equation in two variables
Not a linear equation in two variables

6. The equation A𝑥 + 𝐵𝑦 + 𝐶 = 0, where 𝐴, 𝐵, and 𝐶 are constants,
𝐴 ≠ 0, 𝐵 ≠ 0 and 𝑥, 𝑦 are variables, can be written as follows:
From the equation A𝑥 + 𝐵𝑦 + 𝐶 = 0
A𝑥 + 𝐵𝑦 + 𝐶 = −𝐶
Let 𝐴 = 𝑎, 𝐵 = 𝑏, −𝐶 = 𝑐
We get a𝑥 + 𝑏𝑦 = 𝑐

7. The equation A𝑥 + 𝐵𝑦 + 𝐶 = 0, where 𝐴, 𝐵 are not simultaneously
equal to zero, besides rewriting it in the form a𝑥 + 𝑏𝑦 = 𝑐
we can also rewrite it in another form as follows:
From the equation A𝑥 + 𝐵𝑦 + 𝐶 = 0
A𝑥 + 𝐵𝑦 + 𝐶 = −𝐴𝑥 − 𝐶
A𝑥 + 𝑦 + 𝐶 = −
𝐴
𝐵
𝑥 −
𝐶
𝐵
Let, 𝑎 = −
𝐴
𝐵
We get
𝑏 = −
𝐶
𝐵
𝑦 = −
𝐴
𝐵
𝑥 −
𝐶
𝐵
𝑦 = 𝑎𝑥 + 𝑏

8. A linear equation in two variables, when 𝑥, 𝑦 are variables, can be
written in many forms as follows:
1. A𝑥 + 𝐵𝑦 + 𝐶 = 0, where 𝐴, 𝐵, and 𝐶 are constants, and 𝐴 and 𝐵
are not simultaneously equal to zero.
2. a𝑥 + 𝑏𝑦 = 𝑐, where 𝑎, 𝑏, and 𝑐 are constants, and 𝑎 and 𝑏 are not
simultaneously equal to zero.
3. 𝑦 = 𝑎𝑥 + 𝑏, where 𝑎 and 𝑏 are constants, and 𝑎 is called the
coefficient of 𝑥.

9. Solutions to the Linear
Equations in Two variables

10. Solutions to the Linear Equations in Two variables
2𝑥 + 3 = 7
2𝑥 = 7 − 3
2𝑥 = 4
𝑥 = 2
𝑥 + 𝑦 = 8
𝑥
𝑦
1 3
80
4
807
2
6
3
5
4
4
5
3
6
2
7
1
or 𝑦 = 8 − 𝑥
The solution to the equation is the
value of 𝑥 that satisfies the equation
The solution to the equation is the
values of 𝑥 and 𝑦 that satisfies the
equation
1,7 2,6 3,5 4,4 5,3 6,2 7,1

11. The solutions to the linear equations in two
variables in the form 𝑎𝑥 + 𝑏𝑦 = 𝑐, where 𝑥
and 𝑦 are variables, are the values of 𝑥 and
𝑦 that make the equation true.
A linear equation in one variable has only
one solution.

12. “The number of male students is 5 people more than the number
of female students.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
(2) If the total number of students is not more than 19, write the
ordered pairs that are solutions to the equation in (1)
(3) How many solutions are there based on the condition in (2),
why?

13. “The number of male students is 5 people more than the number
of female students.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
Let 𝑥 be the number of male students
𝑦 be the number of female students
𝑥 = 𝑦 + 5

14. “The number of male students is 5 people more than the number
of female students.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
(2) If the total number of students is not more than 19, write the
ordered pairs that are solutions to the equation in (1)
𝑥
𝑦
5 3
80
4
800
6
1
7
2
8
3
9
4
10
5
11
6
4
80
12
7
5,0 6,1 7,2 8,3 9,4 10,5 11,6 12,7
𝑥 = 𝑦 + 5

15. “The number of male students is 5 people more than the number
of female students.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
(2) If the total number of students is not more than 19, write the
ordered pairs that are solutions to the equation in (1)
5,0 6,1 7,2 8,3 9,4 10,5 11,6 12,7
(3) How many solutions are there based on the condition in (2),
why?
There are 8 solutions because the total number of students is 5 or
more, but not more than 19.
𝑥 = 𝑦 + 5

16. “The length of a rectangle is twice its width.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
(2) Write the ordered pairs that are solutions to the equation in (1)
(3) How many solutions are there to the equation in (1)?

17. “The length of a rectangle is twice its width.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
Let 𝑥 be the width of the rectangle
𝑦 be length of the rectangle
𝑦 = 2𝑥

18. “The length of a rectangle is twice its width.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
(2) Write the ordered pairs that are solutions to the equation in (1)
𝑥
𝑦
1
2
2
4
3
6
4
8
5
10
1,2 2,4 3,6 4,8 5,10 6,12
𝑦 = 2𝑥
6
12

19. “The length of a rectangle is twice its width.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
(2) Write the ordered pairs that are solutions to the equation in (1)
1,2 2,4 3,6 4,8 5,10 6,12
𝑦 = 2𝑥
(3) How many solutions are there to the equation in (1)?
𝑥 and 𝑦 are real numbers which are greater than zero.
The number of solutions to this equation is then infinite.

20. “Karn and Patcha brought some red beans to school for their
agriculture class. The total weight of their beans was 3 kilograms.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
(2) Write the ordered pairs that are solutions to the equation in (1)
(3) How many solutions are there to the equation in (1)?

21. “Karn and Patcha brought some red beans to school for their
agriculture class. The total weight of their beans was 3 kilograms.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
Let 𝑥 be weight of the beans brought by Karn
𝑦 be the weight of the beans brought by Patcha
𝑥 + 𝑦 = 3

22. “Karn and Patcha brought some red beans to school for their
agriculture class. The total weight of their beans was 3 kilograms.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
(2) Write the ordered pairs that are solutions to the equation in (1)
𝑥
𝑦
0.5
2.5
1
2
1.5
1.5
2
1
2.5
0.5
0.5,2.5 1,2 1.5,1.5 2,1 2.5,0.5
𝑥 + 𝑦 = 3

23. “Karn and Patcha brought some red beans to school for their
agriculture class. The total weight of their beans was 3 kilograms.”
(1) Rewrite the above sentence into an equation form using 𝑥 and
𝑦 as the variables.
(2) Write the ordered pairs that are solutions to the equation in (1)
0.5,2.5 1,2 1.5,1.5 2,1 2.5,0.5
𝑥 + 𝑦 = 3
(3) How many solutions are there to the equation in (1)?
𝑥 and 𝑦 are real numbers which are greater than zero.
The number of solutions to this equation is then infinite.

24. Graphs of Linear
Equations in Two variables

25. 15
2
3
4
5
6
7
8
9
10
11
12
13
1
14
16
5−3 −2 −3 0 1 2 3 4 6 7 8 9 10 11 12−6 −5 −4
𝑥
𝑦
Consider the equation 𝑥 + 𝑦 = 8, when 𝑥 is any integer from −3 t0 3.
𝑥
𝑦
-3 3
80
4
8011
-2
10
-1
9
0
8
1
7
2
6
3
5

26. 15
2
3
4
5
6
7
8
9
10
11
12
13
1
14
16
5−3 −2 −3 0 1 2 3 4 6 7 8 9 10 11 12−6 −5 −4
𝑥
𝑦
Consider the equation 𝑥 + 𝑦 = 8, when 𝑥 is any integer from −3 t0 3.
𝑥
𝑦
-3 3
80
4
8011
-2
10
-1
9
0
8
1
7
2
6
3
5
When 𝑥 is any integer less than −3.
𝑥
𝑦
…
…
-6
14
-5
13
-4
12
When 𝑥 is any integer more than 3.
𝑥
𝑦
4
4
5
3
6
2
…
…
When 𝑥 is any real number.

27. The graph of the linear equation in the form
𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0, where 𝑥 and 𝑦 are
variables, is a straight line passing through
all ordered pairs, which are solutions to the
equation.
We call the graph of a linear equation in two
variables a straight-line graph.

28. 1 2 3 4 5
0
−1−2−3−4
−1
−2
−3
1
2
3
4
5
6
𝑥
𝑦
1. Plot the graph of the equation 𝑦 = 𝑥 + 1, where 𝑥 and 𝑦 are any real
numbers: 3
80
4
80
𝑥
𝑦
-3
-2
-2
-1
-1
0
0
1
1
2
2
3
3
4
1. Is the point 1,2 on the straight line L?L
2. Do 𝑥 = 1 and 𝑦 = 2 make the equation
𝑦 = 𝑥 + 1 true?
3. Is the point 3,2 on the straight line L?
4. Do 𝑥 = 3 and 𝑦 = 2 make the equation
𝑦 = 𝑥 + 1 true?
5. If point 𝑎, 𝑏 is on the straight line L,
do 𝑥 = 𝑎 and 𝑦 = 𝑏 make the
equation 𝑦 = 𝑥 + 1 true?
6. If point 𝑎, 𝑏 is not on the straight
line L, do 𝑥 = 𝑎 and 𝑦 = 𝑏 make the
equation 𝑦 = 𝑥 + 1 true?
• Yes
• Yes
• No
• No
• Yes• No

29. If a point 𝑎, 𝑏 is on a graph of a linear
equation in two variables, when 𝑥 is
substituted with 𝑎 and 𝑦 is substituted by 𝑏
in the equation, the equation is true.
If a point 𝑎, 𝑏 is not on the graph, the
substitutions will make the equation is false.

30. 2. From the equation 4𝑥 + 5𝑦 = 23, are the following ordered pairs on the
graph of the equation?
1. 2,3
2. 5,1
If 𝑥 is substituted by 2 and 𝑦 is substituted by 3, we get
4𝑥 + 5𝑦 = 23
4 2 + 5 3 = 23
8 + 15 = 23
23 = 23 TRUE
Therefore, 2,3 is on the graph of the equation 4𝑥 + 5𝑦 = 23.
If 𝑥 is substituted by 5 and 𝑦 is substituted by 1, we get
4𝑥 + 5𝑦 = 23
4 5 + 5 1 = 23
20 + 5 = 23
25 = 23 FALSE
Therefore, 2,3 is not on the graph of the equation 4𝑥 + 5𝑦 = 23.

31. 3. Rewrite the equation 2𝑥 − 𝑦 − 3 = 0 in the form of 𝑦 = 𝑎𝑥 + 𝑏 and find the
values of 𝑎 and 𝑏.
2𝑥 − 𝑦 − 3 = 0
y = 2𝑥 − 3
By comparing the above equation to 𝑦 = 𝑎𝑥 + 𝑏, we get
𝑎 = 2 and 𝑏 = −3

32. 4. Plot the graph of the equation 2𝑥 − 𝑦 + 4 = 0
3
80
4
80
𝑥
𝑦
-2
0
-1
2
0
4
1
6
2
8
1 2 3 4 5
0
−1−2−3−4
−1
−2
−3
1
2
3
4
5
6
7
8
𝑥
𝑦
2𝑥 − 𝑦 + 4 = 0
𝑦 = 2𝑥 + 4

33. 4. Plot the graph of the equation 2𝑥 − 𝑦 + 4 = 0
𝑥
𝑦
-2
0
2
8
1 2 3 4 5
0
−1−2−3−4
−1
−2
−3
1
2
3
4
5
6
7
8
𝑥
𝑦
2𝑥 − 𝑦 + 4 = 0
𝑦 = 2𝑥 + 4

34. 5. Plot the graph of the equation 3𝑥 + 𝑦 + 3 = 0, where 𝑥 and 𝑦 are real numbers
3𝑥 + 𝑦 + 3 = 0
y = −3𝑥 − 3
𝑥
𝑦
-1
0
1
-6
1 2 3 4 5
0
−1−2−3−4
−2
−4
−6
2
4
6
8
𝑥
𝑦
0
-3

35. The graph of a linear equation in two
variables 𝑎𝑥 + 𝑏𝑦 = 𝑐, where 𝑎 ≠ 0, 𝑏 ≠ 0,
is a straight line intercepting the 𝑥 −axis and
𝑦 −axis.
If 𝑥 = 0, 𝑦 =
𝑐
𝑏
the 𝑦 −intercept is 0,
𝑐
𝑏
If 𝑦 = 0, 𝑥 =
𝑐
𝑎
the 𝑥 −intercept is
𝑐
𝑎
, 0

36. 5. Plot the graph of the equation 3𝑥 + 𝑦 + 3 = 0, where 𝑥 and 𝑦 are real numbers
3𝑥 + 𝑦 + 3 = 0
y = −3𝑥 − 3
𝑥
𝑦
-1
0
0
-3
1
-6
1 2 3 4 5
0
−1−2−3−4
−2
−4
−6
2
4
6
8
𝑥
𝑦
If 𝑥 = 0, 𝑦 = −3
If 𝑦 = 0, 𝑥 = −1
The 𝑦 − intercept is 0, −3
The 𝑥 − intercept is −1, 0
The 𝑦 − intercept is a point
where the line intersects the
𝑦 −axis.
The 𝑥 − intercept is a point
where the line intersects the
𝑥 −axis.

37. 6. Plot the graph of the equation 𝑥 + 2𝑦 − 6 = 0, where 𝑥 and 𝑦 are real numbers
𝑥 + 2𝑦 − 6 = 0
y = −
𝑥
2
+ 3
𝑥
𝑦
-2
4
0
3
2
2
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
6
𝑥
𝑦
If 𝑥 = 0, 𝑦 = 3
If 𝑦 = 0, 𝑥 = 6
The 𝑦 − intercept is 0, 3
The 𝑥 − intercept is 6, 0

38. 7. Find the 𝑥-intercept and 𝑦-intercept of the equation 3𝑥 + 4𝑦 − 12 = 0.
If 𝑥 = 0, we get 3𝑥 + 4𝑦 − 12 = 0
3𝑥 + 4𝑦 − 12 = 0
4𝑦 = 12
𝑦 = 3
The 𝑦 −intercept is 0,3
If 𝑦 = 0, we get 3𝑥 + 4𝑦 − 12 = 0
3𝑥 + 3𝑥 − 12 = 0
3𝑥 = 12
𝑥 = 4
The 𝑥 −intercept is 4,0

39. 8. Plot the graphs of the following equations on the same coordinate plane.
𝑦 = 2𝑥 + 4
𝑦 = 2𝑥 + 6
𝑦 = 2𝑥 − 4
𝑦 = 2𝑥
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
5
6
𝑥
𝑦
−4
If 𝑥 = 0, 𝑦 = 4, 𝑦 −intercept 0,4
If 𝑦 = 0, 𝑥 = −2, 𝑥 − intercept −2,0
If 𝑥 = 0, 𝑦 = 6, 𝑦 − intercept 0,6
If 𝑦 = 0, 𝑥 = −3, 𝑥 − intercept −3,0
If 𝑥 = 0, 𝑦 = −4,
If 𝑦 = 0, 𝑥 = 2,
𝑦 − intercept 0, −4
𝑥 − intercept 2,0
If 𝑥 = 0, 𝑦 = 0,
If 𝑦 = 0, 𝑥 = 0,
𝑦 − intercept 0,0
𝑥 − intercept 0,0
If 𝑥 = 1, 𝑦 = 2
𝑦 = 2𝑥 + 4
𝑦 = 2𝑥 + 6
𝑦 = 2𝑥 − 4
𝑦 = 2𝑥

40. 8. Plot the graphs of the following equations on the same coordinate plane.
What is the coefficient of 𝑥 in the equation 𝑦 =
2𝑥 + 6?
The coefficient of 𝑥 is 2.
Are the coefficients of 𝑥 in the equations 𝑦 = 2𝑥 +
4, 𝑦 = 2𝑥 + 6, 𝑦 = 2𝑥 − 4 and
𝑦 = 2𝑥 the same?
Yes
Are the graphs of the equations 𝑦 = 2𝑥 + 4, 𝑦 =
2𝑥 + 6, 𝑦 = 2𝑥 − 4 and
𝑦 = 2𝑥 parallel?
Yes
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
5
6
𝑥
𝑦
−4
𝑦 = 2𝑥 + 4
𝑦 = 2𝑥 + 6
𝑦 = 2𝑥 − 4
𝑦 = 2𝑥

41. 8. Plot the graphs of the following equations on the same coordinate plane.
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
5
6
𝑥
𝑦
−4
𝑦 = 2𝑥 + 4
𝑦 = 2𝑥 + 6
𝑦 = 2𝑥 − 4
𝑦 = 2𝑥
If two linear equations in two
variables are in the form of 𝑦 =
𝑎𝑥 + 𝑏 and 𝑦 = 𝑎𝑥 + 𝑑 where 𝑏 ≠ 𝑑,
and 𝑎, 𝑏, 𝑑 are real numbers, the
graphs of the equations are parallel.
What will the graphs of the two equations
look like if 𝑏 = 𝑑?

42. 9. Plot the graphs of the equations 𝑦 = 2𝑥 − 5 and 𝑦 = −
1
2
𝑥 +
5
2
on the same
coordinate plane and indicate the point where the graphs cross each other.
𝑦 = 2𝑥 − 5
𝑦 = −
1
2
𝑥 +
5
2
If 𝑥 = 0, 𝑦 = −5, 𝑦 −intercept 0, −5
If 𝑦 = 0, 𝑥 =
5
2 𝑥 − intercept
5
2
, 0
If 𝑥 = 0, 𝑦 =
5
2
, 𝑦 − intercept 0,
5
2
If 𝑦 = 0, 𝑥 = 5, 𝑥 − intercept 5,0
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4
3,1

43. 10. Plot the graphs of the equations 𝑦 = 𝑥 + 2 and 𝑦 = 2𝑥 + 2 on the same
coordinate plan.
𝑦 = 𝑥 + 2 If 𝑥 = 0, 𝑦 = 2, 𝑦 −intercept 0,2
If 𝑦 = 0, 𝑥 = −2 𝑥 − intercept −2, 0
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4
𝑦 = 2𝑥 + 2 If 𝑥 = 0, 𝑦 = 2, 𝑦 − intercept 0, 2
If 𝑦 = 0, 𝑥 = −1, 𝑥 − intercept −1, 0

44. 10. Plot the graphs of the equations 𝑦 = 𝑥 + 2 and 𝑦 = 2𝑥 + 2 on the same
coordinate plan.
Compare the equations 𝑦 = 𝑥 + 2 and y = 2𝑥 + 2
to the equation 𝑦 = 𝑎𝑥 + 𝑏. What are the values of
𝑎 in every equation? Are they more or less than
zero?
−3
1 2 3 4 50
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4
The values of 𝑎 in every equation are more than
zero.
Do the angles between the 𝑥 −axis and each of the
graphs make acute or obtuse angles ? (The angles
are measured counterclockwise to the graphs)
Both graphs make acute angles to the 𝑥 −axis

45. 10. Plot the graphs of the equations 𝑦 = 𝑥 + 2 and 𝑦 = 2𝑥 + 2 on the same
coordinate plan.
For a linear equation in two
variables 𝑦 = 𝑎𝑥 + 𝑏,
where 𝑎 > 0, the graph of the
equation makes an acute angle to
the 𝑥 −axis.
−3
1 2 3 4 50
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4

46. 11. Plot the graphs of the equations 𝑦 = −𝑥 + 3 and 𝑦 = −2𝑥 + 2 on the same
coordinate plan.
𝑦 = −𝑥 + 3 If 𝑥 = 0, 𝑦 = 3, 𝑦 −intercept 0,3
If 𝑦 = 0, 𝑥 = 3 𝑥 − intercept 3, 0
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4
𝑦 = −2𝑥 + 2 If 𝑥 = 0, 𝑦 = 2, 𝑦 − intercept 0, 2
If 𝑦 = 0, 𝑥 = 1, 𝑥 − intercept 1, 0

47. 11. Plot the graphs of the equations 𝑦 = −𝑥 + 3 and 𝑦 = −2𝑥 + 2 on the same
coordinate plan.
Compare the equations𝑦 = −𝑥 + 3 and 𝑦 =
− 2𝑥 + 2 to the equation 𝑦 = 𝑎𝑥 + 𝑏. What are
the values of 𝑎 in every equation? Are they more
or less than zero?
The values of 𝑎 in every equation are less than
zero.
Do the angles between the 𝑥 −axis and each of the
graphs make acute or obtuse angles ? (The angles
are measured counterclockwise to the graphs)
Both graphs make obtuse angles to the 𝑥 −axis
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4

48. 11. Plot the graphs of the equations 𝑦 = −𝑥 + 3 and 𝑦 = −2𝑥 + 2 on the same
coordinate plan.
For a linear equation in two
variables 𝑦 = 𝑎𝑥 + 𝑏,
where 𝑎 < 0, the graph of the
equation makes an obtuse angle to
the 𝑥 −axis.
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4

49. 12. Plot the graphs of the equations 𝑦 = 1, 𝑦 = 2 and 𝑦 = 3 on the same
coordinate plan.
𝑦 = 1
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4
If 𝑥 = −1, 𝑦 = 1
𝑦 = 0 𝑥 + 1
If 𝑥 = 0, 𝑦 = 1
If 𝑥 = 1, 𝑦 = 1
𝑦 = 2
If 𝑥 = −1, 𝑦 = 2
𝑦 = 0 𝑥 + 2
If 𝑥 = 0, 𝑦 = 2
If 𝑥 = 1, 𝑦 = 2
𝑦 = 3
If 𝑥 = −1, 𝑦 = 3
𝑦 = 0 𝑥 + 3
If 𝑥 = 0, 𝑦 = 3
If 𝑥 = 1, 𝑦 = 3

50. 12. Plot the graphs of the equations 𝑦 = 1, 𝑦 = 2 and 𝑦 = 3 on the same
coordinate plan.
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4
The graph of an equation 𝑦 = 𝑐,
where 𝑐 is any real number, is a
horizontal straight line, which is
parallel to the 𝑥 −axis. The graph
intersects the 𝑦 −axis at 0, 𝑐

51. 13. Plot the graphs of the equations 𝑥 = 4, and 𝑥 = −2 on the same
coordinate plan.
𝑥 = 4
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4
If 𝑦 = −1, 𝑥 = 4
𝑥 + 0 𝑦 = 4
If 𝑦 = 0, 𝑥 = 4
If 𝑦 = 1, 𝑥 = 4
𝑥 = −2
If 𝑦 = −1, 𝑥 = −2
𝑥 + 0 𝑦 = −2
If 𝑦 = 0, 𝑥 = −2
If 𝑦 = 1, 𝑥 = −2

52. 13. Plot the graphs of the equations 𝑥 = 4, and 𝑥 = −2 on the same
coordinate plan.
−3
1 2 3 4 5
0
−1−2−3−4
−1
−2
1
2
3
4
−5
𝑥
𝑦
−4
The graph of an equation 𝑥 = 𝑚,
where 𝑚 is any real number, is a
vertical straight line, which is
parallel to the 𝑦 −axis. The graph
intersects the 𝑥 −axis at 𝑚, 0