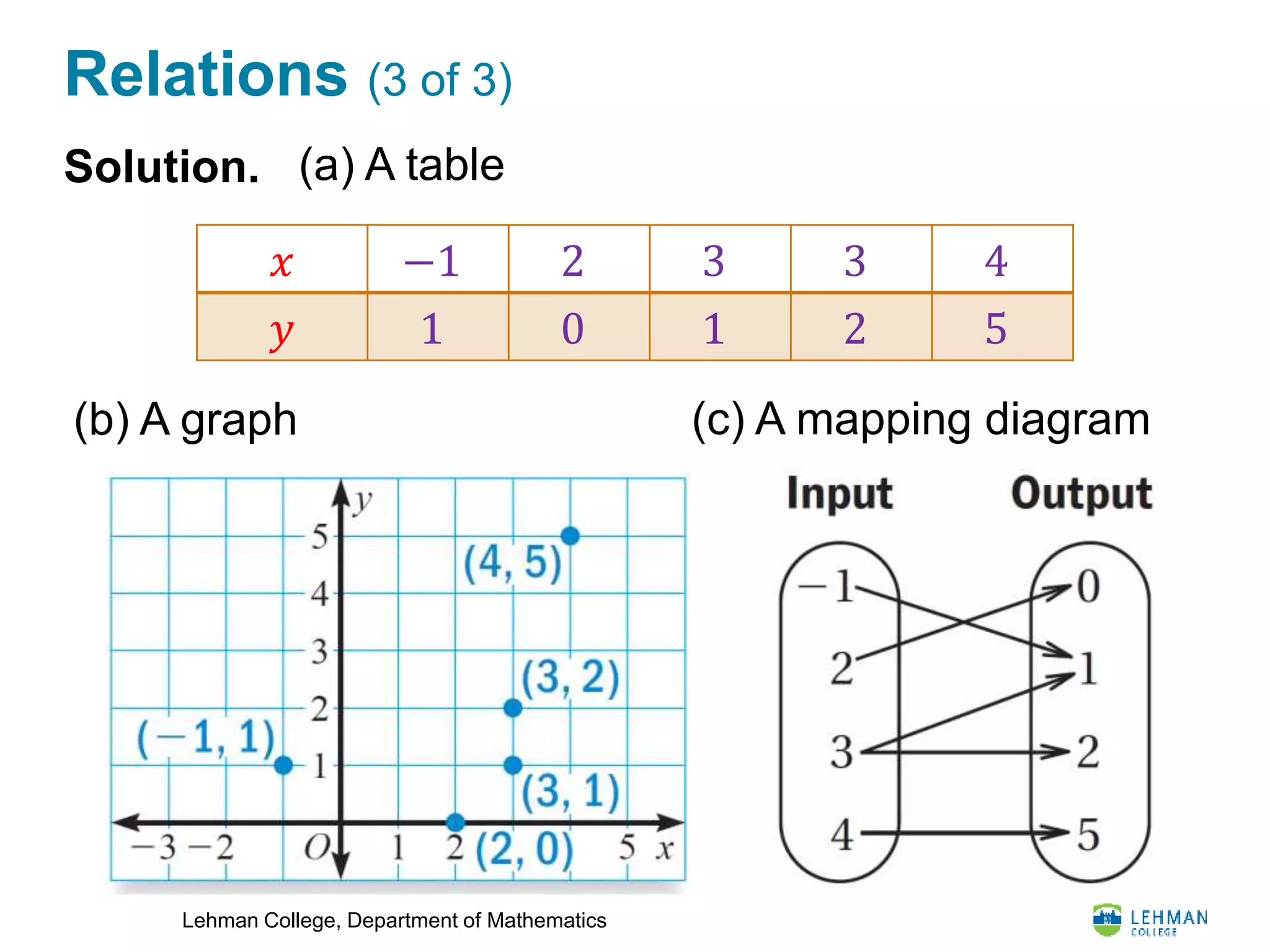
This document discusses functions and function notation. It defines a function as a relation where each input has exactly one output. Functions are represented using functional notation f(x) where f is the name of the function and x is the input. The domain of a function is the set of all possible inputs, and the range is the set of all possible outputs. A relation is not a function if one input has more than one output. The natural domain of a function is the set of inputs that make the function definition valid.

1. 𝐏𝐓𝐒 𝟑
Bridge to Calculus Workshop
Summer 2020
Lesson 11
Functions and
Function Notation
“Mathematics is the art of giving
the same name to different things”
- Henri Poincaré -

2. Lehman College, Department of Mathematics
Relations (1 of 3)
A relation is a pairing of numbers from one set, called
the domain, with numbers from another set, called the
range. Each number in the domain is an input. Each
number in the range is an output.
In relations represented by ordered pairs, the inputs are
the 𝑥-coordinates and the outputs are the 𝑦-coordinates
Example 1. State the domain and range of the relation:
Solution.
𝑥 2 4 5 5 7
𝑦 5 9 3 7 7
2, 4, 5, 7Domain: Range: 3, 5, 7, 9

3. Lehman College, Department of Mathematics
Relations (2 of 3)
Example 2. Give an example of an ordered pair from
each of the following relations. Determine the domain
and range of the relations:
Solution.
Example 3. Represent the following relation as:
−1, 1 , 2, 0 , 3, 1 , 3, 2 , 4, 5
(a) A table (b) A graph (c) A mapping diagram
(a) 𝑦 = 𝑥2
+ 1 (b) 𝑦 = 𝑥
(a) 1, 2 Domain: ℝ Range: 𝑥 ≥ 1
(b) 4, 2 Domain: 𝑥 ≥ 0 Range: 𝑥 ≥ 0

4. Lehman College, Department of Mathematics
Relations (3 of 3)
Solution.
𝑥 −1 2 3 3 4
𝑦 1 0 1 2 5
(a) A table
(b) A graph (c) A mapping diagram

5. Lehman College, Department of Mathematics
Function Definition (1 of 1)
A relation is a function if for each input, there is exactly
one output. In this case, we say the output is a function
of the input.
Example 4. State which relation is a function:
Solution.
2, 36 , 4, 38 , 5, 40 , 5, 41 , 7, 42
−1, 1 , 2, 0 , 3, 1 , 3, 2 , 4, 5
(a)
(b)
(c) −2, 3 , −1, 5 , 0, 7 , 1, 9 , 2 11
(a) is not a function because:
the input 5 is paired with two different outputs 40, & 41.
Alligators of the same age can have different heights.
(b) is not a function because: (3, 1) and (3, 2) are pairs
(c) is a function as: 1 input paired with exactly 1 output.

6. Lehman College, Department of Mathematics
Vertical Line Test (1 of 1)
Vertical Line Test. A relation is not a function, if one
can find a vertical line passing through more than one
point on its graph. Otherwise, the relation is a function.
(a) This is a function, as no
vertical line passes through
more than one point.
(b) Not a function since a
vertical line passes through
the points (3, 1) and (3, −2).

7. Lehman College, Department of Mathematics
Function Notation (1 of 6)
If an equation in 𝑥 and 𝑦 gives one and only one value
of 𝑦 for each value of 𝑥, then the variable 𝑦 is a function
of the variable 𝑥.
Example 5. In the following relation is 𝑦 a function of 𝑥?
Solution. Note that the ordered pairs 0, 1 and 0, −1
satisfy the equation. Therefore, 𝑦 is not a function of 𝑥.
When an equation represents a function, the function is
often named by a letter such as 𝑓, 𝑔, ℎ. Any letter
(Latin, Greek, other) can be used to name a function.
Let 𝑓 denote a function, then the domain is the set of
inputs and the range—the set of outputs of 𝑓.
𝑥2
+ 𝑦2
= 1

8. Lehman College, Department of Mathematics
Function Notation (2 of 6)
As shown in the following figure (the function machine),
input is represented by 𝑥 and the output by 𝑓(𝑥).
The special notation 𝑓(𝑥), read as “𝑓 of 𝑥” or “𝑓 at 𝑥,”
represents the value of the function at the number 𝑥.
Let us consider an example of a function:
𝑦 = 𝑥2
+ 3𝑥 + 1

9. Lehman College, Department of Mathematics
Function Notation (3 of 6)
We will call this function 𝑓. In our new notation:
Read as: “𝑓 of 𝑥 equals 𝑥-squared plus three-𝑥 plus 1”.
Suppose we wish to find the value of 𝑓(2). We will
substitute the number 2 for 𝑥 in the formula for 𝑓(𝑥):
The statement 𝑓 2 = 11, read as “𝑓 of 2 equals 11”,
tells us that the value of the function at 2 is 11.
𝑓(𝑥) = 𝑥2
+ 3𝑥 + 1
𝑥2
+ 3𝑥 + 1
𝑓(2) = 2 2
+ 3 2 + 1
𝑓(𝑥) =
= 4 + 6 + 1
𝑓(2) = 11

10. Lehman College, Department of Mathematics
Function Notation (4 of 6)
Example 6. For 𝑓 𝑥 = 2𝑥2
− 3𝑥 + 2, evaluate each of
the following:
Solution.
(a) 𝑓(−1) (b) 𝑓(𝑥 + 2) (c) 𝑓(−𝑥)
(a) 𝑓 −1 = 2 −1 2 − 3 −1 + 2
= 2 + 3 + 2 = 7
(b) 𝑓 𝑥 + 2 = 2 𝑥 + 2 2
− 3 𝑥 + 2 + 2
= 2 𝑥2
+ 4𝑥 + 4 − 3 𝑥 + 2 + 2
= 2𝑥2
+ 8𝑥 + 8 − 3𝑥 − 6 + 2
= 2𝑥2
+ 5𝑥 + 4
(c) 𝑓 −𝑥 = 2 −𝑥 2 − 3 −𝑥 + 2 = 2𝑥2
+ 3𝑥 + 2

11. Lehman College, Department of Mathematics
Function Notation (5 of 6)
Example 7. For 𝑓 𝑥 = −3𝑥 + 1, evaluate the difference
quotient:
Solution. Let us first evaluate 𝑓 𝑥 + ℎ :
𝑓 𝑥 + ℎ − 𝑓(𝑥)
ℎ
𝑓 𝑥 + ℎ = −3 𝑥 + ℎ + 1
= −3𝑥 − 3ℎ + 1
𝑓 𝑥 + ℎ − 𝑓 𝑥 = −3𝑥 − 3ℎ + 1 − −3𝑥 + 1
= −3𝑥 − 3ℎ + 1 + 3𝑥 − 1
= −3ℎ
𝑓 𝑥 + ℎ − 𝑓(𝑥)
ℎ
=
−3ℎ
ℎ
= −3 ℎ ≠ 0

12. Lehman College, Department of Mathematics
Function Notation (6 of 6)
Example 8. For 𝑓 𝑥 = 4𝑥 + 𝑥2
, evaluate each of the
following:
Solution.
(a) 𝑓(−3) (b)
𝑓 𝑥 + ℎ − 𝑓(𝑥)
ℎ
(a) 𝑓 −3 = 4 −3 + −3 2
= −12 + 9 =
(b) 𝑓 𝑥 + ℎ = 4 𝑥 + ℎ + 𝑥 + ℎ 2
= 4𝑥 + 4ℎ +
𝑓 𝑥 + ℎ − 𝑓 𝑥 =
−3
𝑥2
+ 2ℎ𝑥 + ℎ2
4𝑥 + 4ℎ + 𝑥2
+ 2ℎ𝑥 + ℎ2 − 4𝑥 + 𝑥2
= 4𝑥 + 4ℎ + 𝑥2 + 2ℎ𝑥 + ℎ2
− 4𝑥 − 𝑥2
= 4ℎ + 2ℎ𝑥 + ℎ2
= ℎ 4 + 2𝑥 + ℎ
𝑓 𝑥 + ℎ − 𝑓(𝑥)
ℎ
=
ℎ 4 + 2𝑥 + ℎ
ℎ
= 4 + 2𝑥 + ℎ ℎ ≠ 0

13. Lehman College, Department of Mathematics
Equality of Functions (1 of 1)
Two functions are equal if they have the same domain
and the same value at every number in that domain.
Example 9. Suppose 𝑓(𝑥) = 𝑥2 with domain all real
numbers and let 𝑔(𝑥) = 𝑥2
with domain the set of
positive numbers. Are 𝑓 and 𝑔 equal as functions?
Answer. No, for example:
does not exist,
Example 10. Suppose 𝑓(𝑥) = 𝑥2
with domain the set
1, 2 and let 𝑔 𝑥 = 3𝑥 − 2 with domain the set 1, 2 .
Are 𝑓 and 𝑔 equal as functions?
Answer.
𝑓 −2 = 4 but 𝑔 −2
Yes, they both have the same domain:
and: 𝑓 1 = 1, 𝑔 1 = 1;
1, 2
𝑓 2 = 𝑔 2 =4, 4.
since, −2 is not in the domain of 𝑔.

14. Lehman College, Department of Mathematics
Equality of Functions (2 of 2)
Given two functions expressed as formulas in 𝑥, how do
you check on what domain they are equal as functions?
Answer. Equate the two formulas and solve for 𝑥.
In Example 10, determine the domain on which the
function 𝑓(𝑥) = 𝑥2
is equal to 𝑔 𝑥 = 3𝑥 − 2.
It follows that 𝑓(𝑥) = 𝑥2
is equal to 𝑔 𝑥 = 3𝑥 − 2 as
functions on the domain:
𝑥2
= 3𝑥 − 2 Equate the two functions
𝑥2
− 3𝑥 + 2 = 0
𝑥 − 1 𝑥 − 2 = 0 Factor
𝑥 = 1, 2 Solve for 𝑥
1, 2

15. Lehman College, Department of Mathematics
Natural Domain of a Function (1 of 1)
If a function defined by a formula does not have a
domain specified, then the “natural domain” or “implied
domain” is the set of real numbers for which the formula
makes sense and produces a real number.
Example 11. Suppose 𝑓(𝑥) = 3𝑥 − 1 2
, determine its
natural domain.
Solution. Substituting any real number for the variable
𝑥, yields a real number for 𝑓(𝑥), so the domain is ℝ.
Example 12. Suppose 𝑓(𝑥) =
𝑥2+3𝑥+7
𝑥−4
, determine its
natural domain.
Solution. The domain of all polynomials is ℝ. So, we
have: 𝑥 − 4 ≠ 0 or 𝑥 ≠ 4, Domain: all reals except 4.

16. Lehman College, Department of Mathematics
Natural Domain of a Function (1 of 1)
Example 13. Let 𝑓(𝑥) = 𝑥, find its natural domain.
Solution. Substituting a negative number for the
variable 𝑥 does not yield a real number for 𝑓(𝑥), so the
natural domain is all nonnegative numbers:
Example 14. Suppose 𝑓(𝑥) = 2𝑥 + 6, determine its
natural domain.
Solution. From Example 13, the expression under the
square root sign must be nonnegative:
𝑥 ≥ 0
2𝑥 + 6 ≥ 0
2𝑥 + 6 − 6 ≥ 0 − 6
2𝑥 ≥ −6
𝑥 ≥ −3