Uploaded byMohammad Tawfik
08 interpolation lagrange
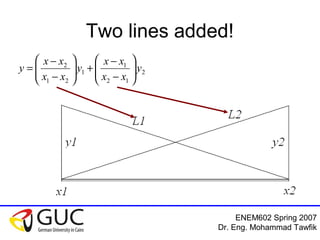
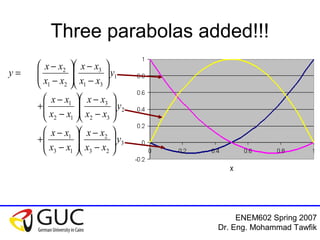
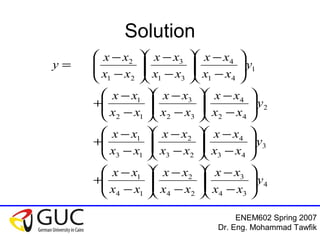
This document contains lecture slides from an ENEM602 engineering mathematics course taught by Dr. Eng. Mohammad Tawfik in Spring 2007. It discusses Lagrange interpolation, which is a method for interpolating a polynomial that passes through a set of points. The document provides examples of using Lagrange interpolation for 2, 3 and 4 points. It derives the general Lagrange interpolation formula and shows an example of applying it to find a 3rd order polynomial to interpolate 4 given data points. Students are assigned homework problems applying Lagrange interpolation.
More Related Content
Similar to 08 interpolation lagrange
08 interpolation lagrange
- 1. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Interpolation Lagrange Interpolation Polynomial
- 2. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Lagrange Method • First, we learned that a polynomial can pass by the points by using a simple polynomial with (n-1) terms. • Then, we learned a way that “looks like” the Taylor expansion (Newton’s method)
- 3. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Lagrange Method (cont’d) • Now, we will use polynomials that are zero at all points except the one we are evaluating at but in an easier form!
- 4. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik For the two points ( ) ( )2211 xxcxxcy −+−= 2 12 1 1 21 2 y xx xx y xx xx y − − + − − = ( ) ( )2121111 xxcxxcy −+−= ( )21 1 2 xx y c − = ( ) ( )2221212 xxcxxcy −+−= ( )12 2 1 xx y c − =
- 5. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Two lines added! 2 12 1 1 21 2 y xx xx y xx xx y − − + − − =
- 6. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Homework • Show that the polynomial obtained by solving a set of equations is equivalent to that obtained by Lagrange method
- 7. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik For the three points ( )( ) ( )( ) ( )( )133 322 211 xxxxc xxxxc xxxxcy −−+ −−+ −−= ( )( ) ( )( ) ( )( )11313 31212 211111 xxxxc xxxxc xxxxcy −−+ −−+ −−= ( )( )312121 xxxxcy −−= ( )( )3121 1 2 xxxx y c −− =
- 8. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Similarly ( )( )1323 3 1 xxxx y c −− = ( )( )3212 2 3 xxxx y c −− =
- 9. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Finally 3 23 2 13 1 2 32 3 12 1 1 31 3 21 2 y xx xx xx xx y xx xx xx xx y xx xx xx xx y − − − − + − − − − + − − − − =
- 10. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Three parabolas added!!! 3 23 2 13 1 2 32 3 12 1 1 31 3 21 2 y xx xx xx xx y xx xx xx xx y xx xx xx xx y − − − − + − − − − + − − − − =
- 11. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Example • Find a 3rd order polynomial to interpolate the function described by the given points using Lagrange’s method x Y -1 1 0 2 1 5 2 16
- 12. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Solution 4 34 3 24 2 14 1 3 43 4 23 2 13 1 2 42 4 32 3 12 1 1 41 4 31 3 21 2 y xx xx xx xx xx xx y xx xx xx xx xx xx y xx xx xx xx xx xx y xx xx xx xx xx xx y − − − − − − + − − − − − − + − − − − − − + − − − − − − =
- 13. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Solution 4 3 2 1 12 1 02 0 12 1 21 2 01 0 11 1 20 2 10 1 10 1 21 2 11 1 01 0 y xxx y xxx y xxx y xxx y − − − − + + + − − − − + + + − − − − + + + −− − −− − −− − =
- 14. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Solution ( )( )( ) ( )( )( ) ( )( )( ) ( )( )( ) 4 3 2 1 6 11 2 21 2 211 6 21 y xxx y xxx y xxx y xxx y −+ + − −+ + −−+ + − −− =
- 15. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Solution ( )( )( ) ( )( )( ) ( )( )( ) ( )( )( )16 6 11 5 2 21 2 2 211 1 6 21 −+ + − −+ + −−+ + − −− = xxx xxx xxx xxx y
- 16. ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Homework #6 • Solve the example presented in the previous lecture (Newton’s method) using Lagrange method • Chapter 18, pp. 505-506, numbers: 18.6, 18.7.