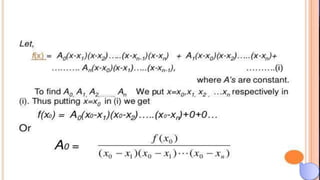The document discusses Lagrange interpolation, a polynomial interpolation method. It introduces Joseph-Louis Lagrange, who developed the method. The method uses Lagrange polynomials to find an nth degree polynomial approximation to a function based on a set of points. The document provides the Lagrange interpolation formula and shows an example of using it. It also discusses inverse interpolation and provides an example. Finally, it outlines the advantages and disadvantages of the Lagrange interpolation method.

1. LAGRANGE INTERPOLATION
METHOD

2. Presented by:
group- 4
Akash Roushann 04
Ayush Raj 15
Md. Imran Alam 27
Sejal 40
Sumit 56
Komal Kumari 59

3. CONTENT
 About Joseph-Louis Lagrange
 Define Lagrange interpolation
 Formula
 Prove
 Question
 Inverse interpolation
 Question
 Advantages & Disadvantage
 Conclusion

4. About Joseph-Louis Lagrange
Joseph Louis Lagrange (1736 -1813) From `A Short
Account of the History of Mathematics' (4th edition, 1908)
by W. W. Rouse Ball. Joseph Louis Lagrange, the greatest
mathematician of the eighteenth century, was born at Turin
on January 25, 1736, and died at Paris on April 10, 1813.

5. Lagrange interpolation
Lagrange polynomials are used for polynomial interpolation.
For a given set of distinct points xj and numbers yj.
Lagrange’s interpolation is also an Nth degree polynomial
approximation to f(x).

6. Formula
 Aaaaaaaaaaaaaaaaaa
 This is called Lagrange's interpolation formula and can be
used and unequal intervals.

11.  Question: Find the value of y when x=9 given
X 5 7 11 13 17
Y 150 392 1452 2366 5202

12. Inverse Interpolation
 Inverse interpolation is defined as the process of finding
the value of the argument corresponding to a given value
of the function lying between two tabulated functional
values.

13.  Question: Find x when f(x)=15
X 5 6 9 11
Y 12 13 14 16

14. (15-13)(15-14)(15-16) (5) + (15-12)(15-14)(15-16) (6) + (15-12)(15-13)(15-16) (9) +
(12-13)(12-14)(12-16) (13-12)(13-14)(13-16) (14-12)(14-13)(14-16)
(15-12)(15-13)(15-14) (11)
(16-12)(16-13)(16-14)

15. Advantages
 The formula is simple and easy to remember.
 There is no need to construct the divided difference table.
 The application of the formula is not speedy.

16. Disadvantage
 There is always a chance to committing some error.
 The calculation provide no check whether the functional
values used the taken correctly or not.

17. Conclusion
 Lagrange has a better performance at the boundaries
which makes it more convenient for real time applications.

18. References
 Wikipedia
 Over IQ
 You tube
 Slide share