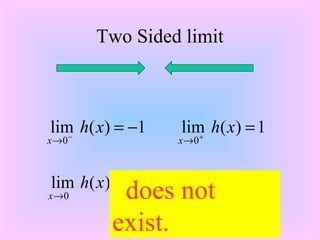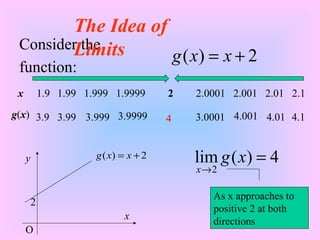
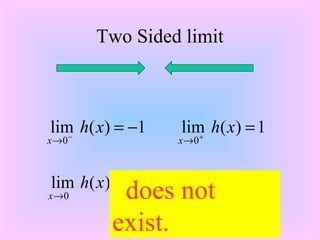
The document discusses the concept of limits. It explains that as the number of sides of a polygon increases, the area of the polygon approximates the area of the circle it is inscribed in, and the limit of the polygon's area is equal to the area of the circle. It also examines the limit of a function as x approaches 2 from both sides, and defines some fundamental rules of limits, such as the constant rule, sum rule, and multiplication rule. Finally, it outlines several techniques that can be used to calculate limits, including direct substitution, factoring, rationalization, and limits involving infinity and trigonometric, exponential and two-sided limits.

1. Limits
“nearness”

2. Consider a polygon inscribed in a circle
The Idea of
Limits

3. n=3 n=4 n=5 n=6 n=7 n=8
‘As number of sides of polygon increases, its area
approximates the area of the circle’
‘limit of Area of polygon is the Area of the circle’
As n approaches infinity ,
Lim Area of polygon = Area of the circle
The Idea of
Limits

4. Consider the
function:
The Idea of
Limits 2)( += xxg
2)( += xxg
x
y
O
2
x 1.9 1.99 1.999 1.9999 2 2.0001 2.001 2.01 2.1
g(x) 3.9 3.99 3.999 3.9999 3.0001 4.001 4.01 4.14
4)(lim
2
=
→
xg
x
As x approaches to
positive 2 at both
directions

5. Fundamental Rules of Limits.
1. The Constant Rule
– When we take the limit of a constant, non-
changing function, the limit will simply be that
constant.
1. The Sum Rule
– If two sequences have limits that exist, then the limit of
the sum of sequences is the sum of the limits of the
sequences.
1. The Multiplication Rule
– If two sequences have limits that exist, then the limit of
the product is the product of the limits.

6. Fundamental Rules of Limits.

7. Techniques in calculating Limits
T1: Limits By Direct Substitution
T2: Limits by Factoring

8. Type 3a: Limits by Rationalization
Techniques in calculating Limits

9. T3b: Limits by Rationalization
Techniques in calculating Limits

10. T4a: Limits at Infinity
Techniques in calculating Limits

11. T4b: Limits at Infinity
Techniques in calculating Limits

12. T5: Trigonometric Limits
Techniques in calculating Limits

13. T6: Limits Involving Number e
Techniques in calculating Limits

14. Try me!!

15. Try me!!

16. Try me!!

17. Try me!!

18. Try me!!

19. 1)(lim
0
−=−
→
xh
x
1)(lim
0
=+
→
xh
x
)(lim
0
xh
x→ does not
exist.
Two Sided limit

20. THANK YOU