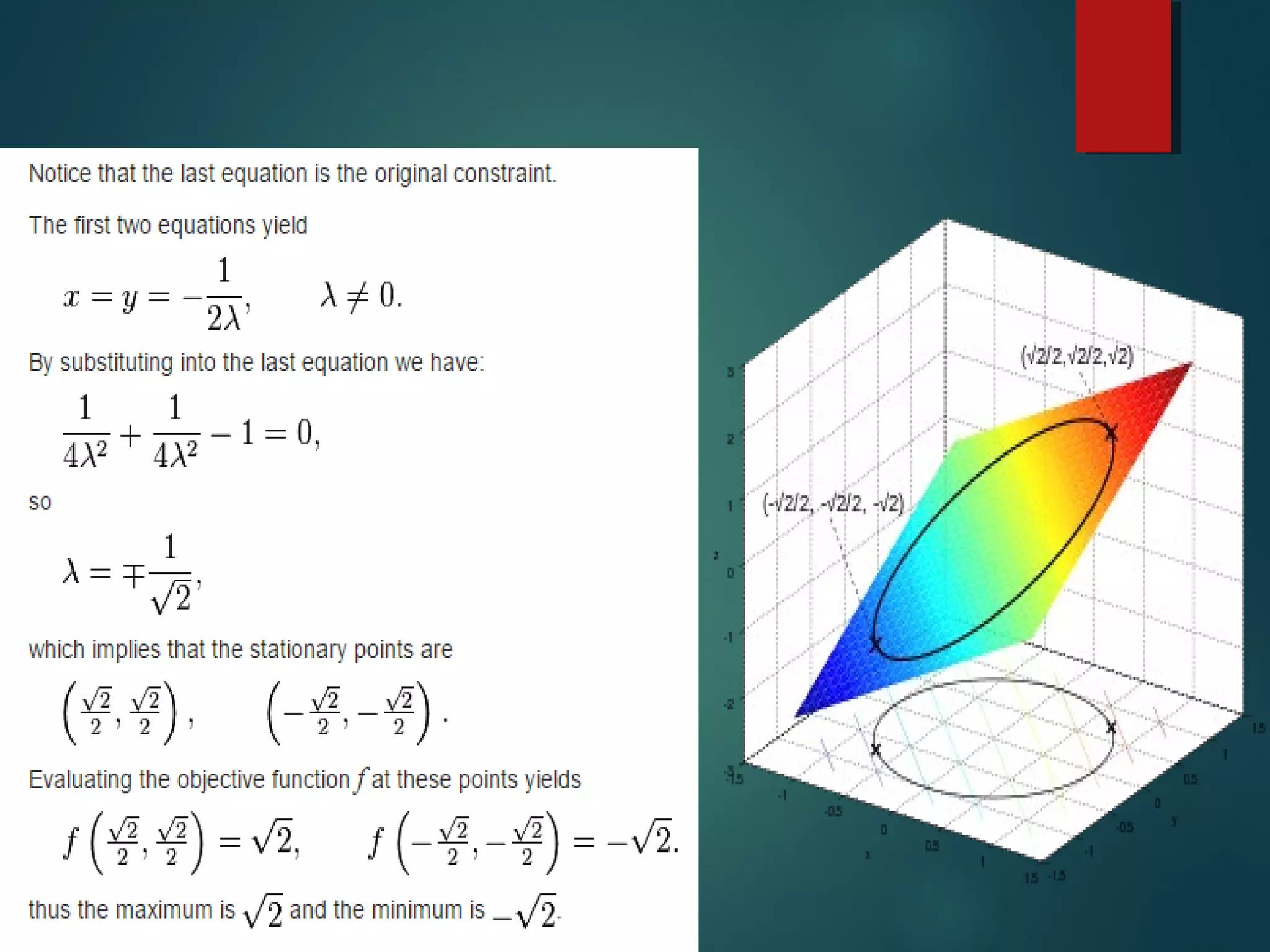
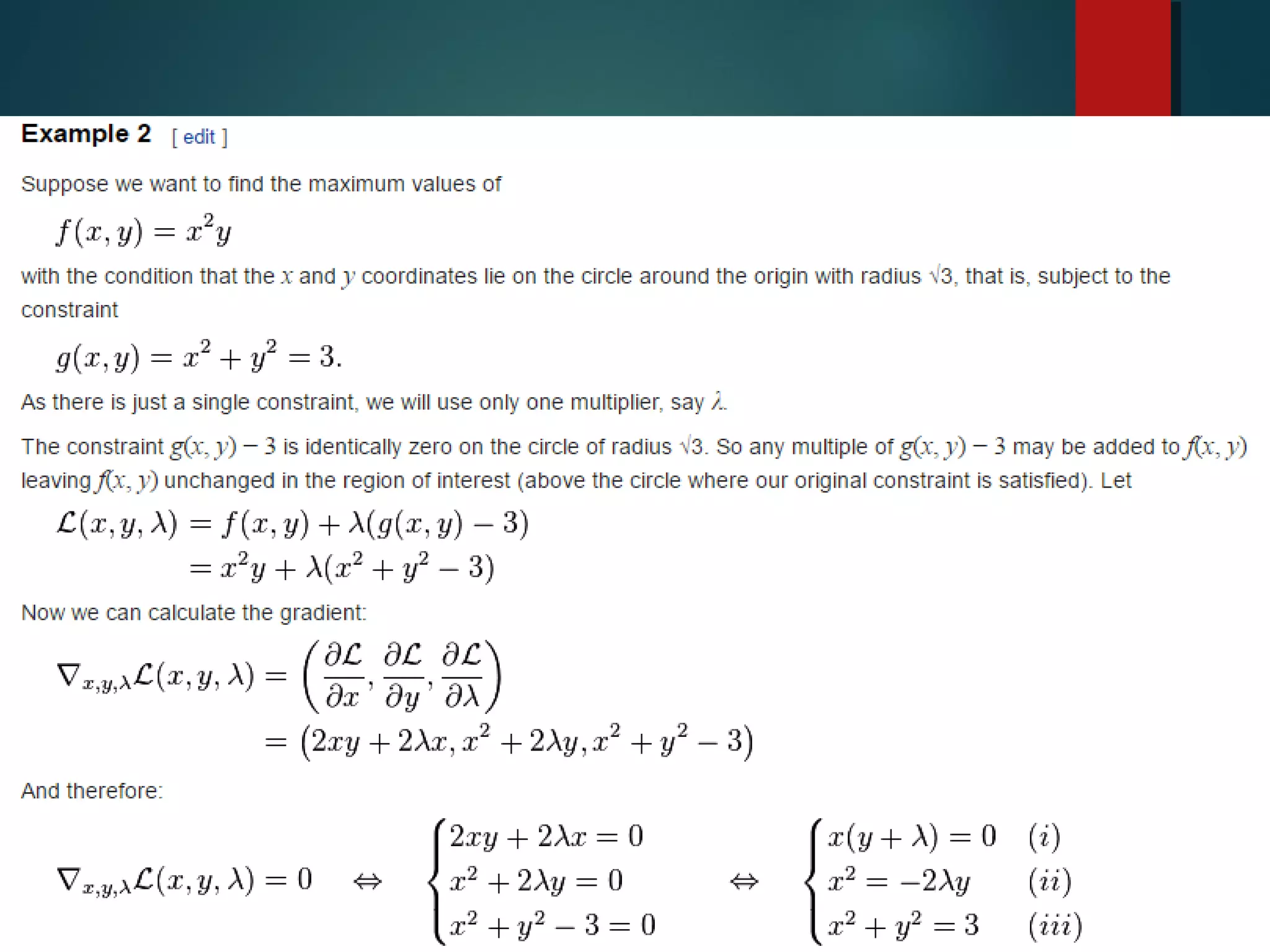
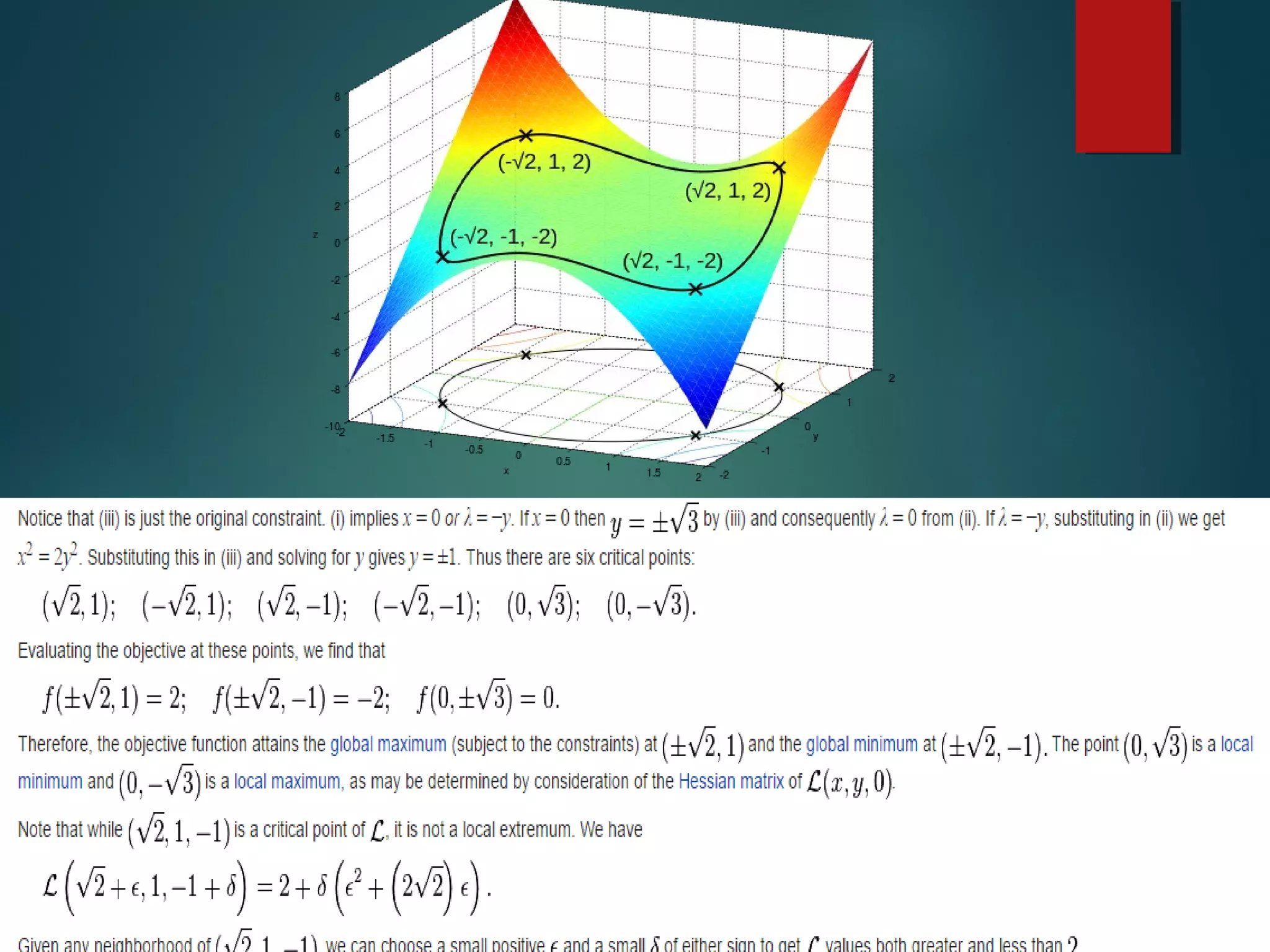
This presentation introduces five presenters and focuses on Lagrange's linear equation and its applications. Specifically, it defines Lagrange's linear partial differential equation as involving a dependent variable z and two independent variables x and y. It also discusses solving linear equations and applications in mathematics, economics, control theory, and nonlinear programming. In economics, the Lagrange multiplier represents the shadow price of a constraint like a budget. In control theory, Lagrange multipliers are interpreted as costate variables in optimal control problems.

1. Welcome To Our Presentation
PRESENTED BY:
1.MAHMUDUL HASSAN - 152-15-5809
2.MAHMUDUL ALAM - 152-15-5663
3.SABBIR AHMED – 152-15-5564
4.ALI HAIDER RAJU – 152-15-5946
5.JAMILUR RAHMAN– 151-15- 5037

2. Presentation On
Lagrange’s equation and its
Application

3. LAGRANGE’S LINEAR EQUATION:
A linear partial differential equation of order one, Involving a
dependent variable z and two independent variables x and y and
is of the form Pp + Qq = R where P, Q, R are the function of x,
y, z.

4. Solution of the linear equation:

7. MATHEMATICAL PROBLEM

12. Applications of Lagrange multipliers

16. Economics
Constrained optimization plays a central role in economics. For
example, the choice problem for a consumer is represented as one of
maximizing a utility function subject to a budget constraint. The
Lagrange multiplier has an economic interpretation as the shadow
price associated with the constraint, in this example the marginal
utility of income. Other examples include profit maximization for a firm,
along with various macroeconomic applications.
Control theory
In optimal control theory, the Lagrange multipliers are interpreted as
costate variables, and Lagrange multipliers are reformulated as the
minimization of the Hamiltonian, in Pontryagin's minimum principle.

17. Nonlinear programming
The Lagrange multiplier method has several generalizations.
In nonlinear programming there are several multiplier rules, e.g., the
Caratheodory-John Multiplier Rule and the Convex Multiplier Rule, for
inequality constraints