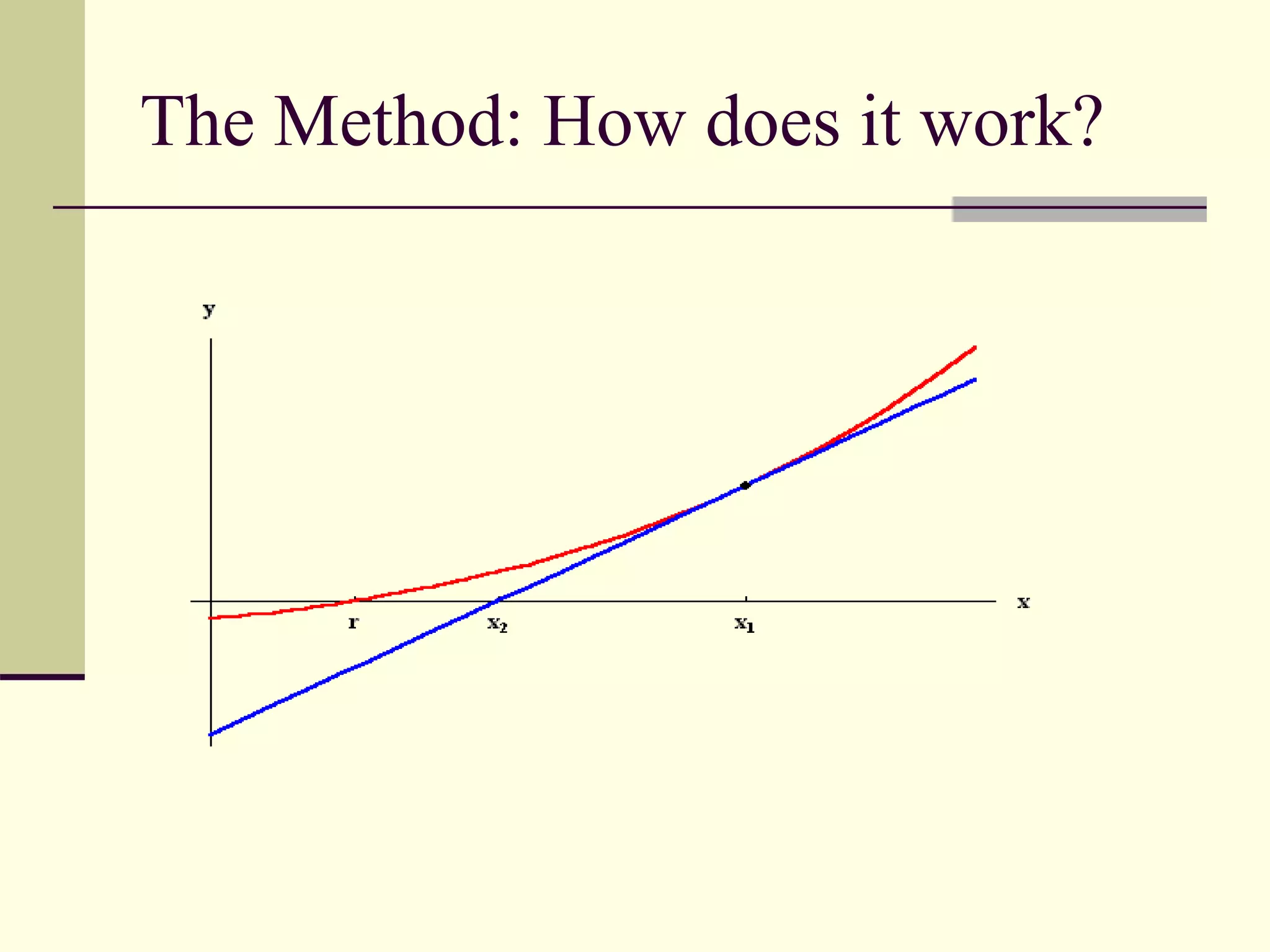
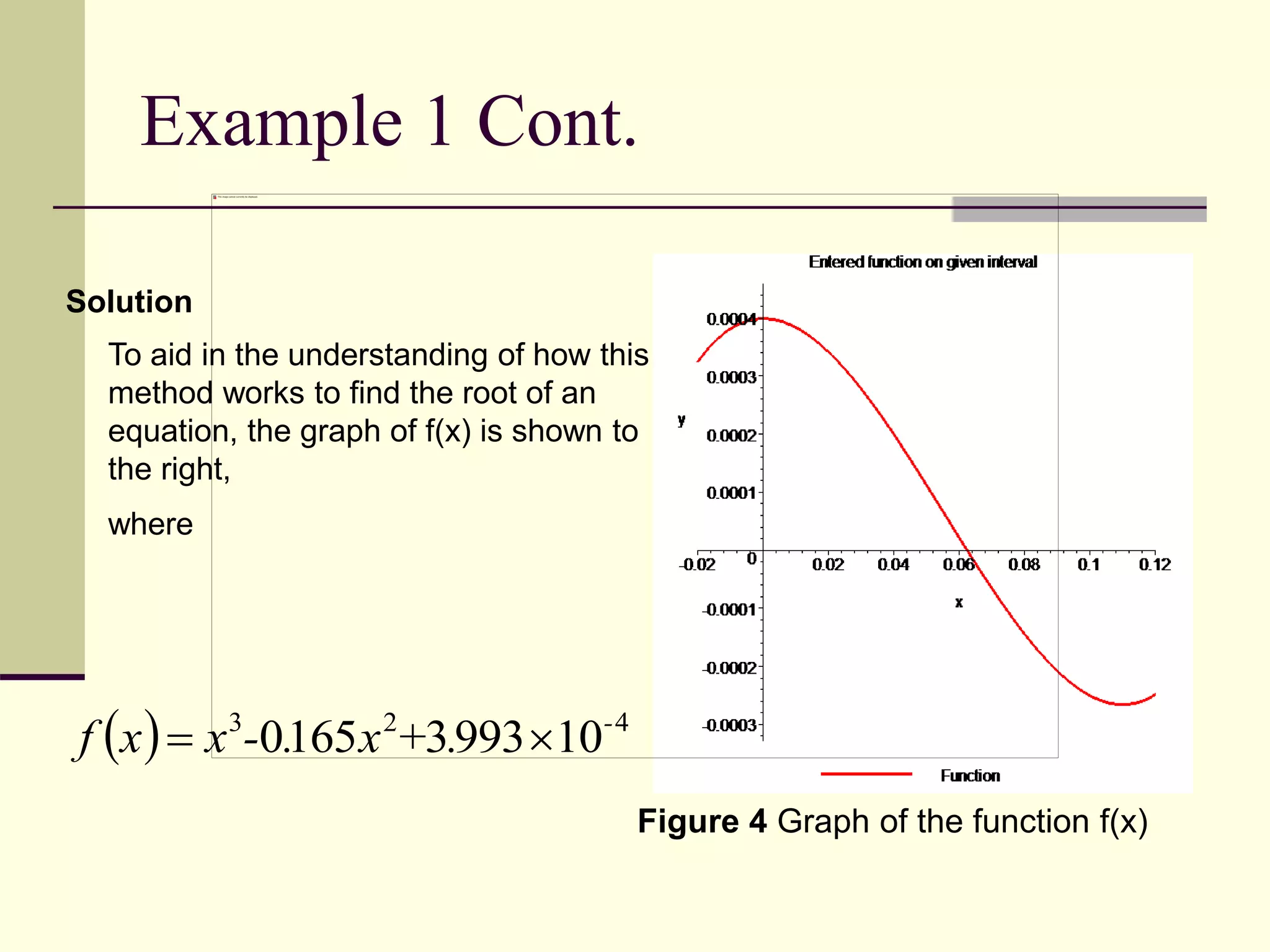
The document discusses the Newton Raphson method for finding roots of equations. It describes how Isaac Newton and Joseph Raphson discovered the method in the 17th century. The method works by taking the derivative of the function and using it to calculate successive approximations that converge on a root. The document provides an example of using the method to find the root of a function and discusses advantages like fast convergence and requiring only an initial guess, as well as potential drawbacks such as failure to converge or slow convergence for roots with multiplicity greater than one.

1. Root Finding Using
Newton Raphson Method

2. Introduction
 History of Newton Raphson’s Method
 The Method
 Example
 Advantages
 Drawbacks
 Summary
 referance

3. History
 Discovered by Isaac Newton and published in
his Method of Fluxions, 1736
 Joseph Raphson described the method in
Analysis Aequationum in 1690
 Method of Fluxions was written earlier in
1671
 Today it is used in a wide variety of subjects,
including Computer Vision and Artificial
Intelligence

4. The Method: How does it work?

5. Formula for finding root:
)(
)(
1
1
12
xf
xf
xx



6. Example
0)cos()(  xxxf
1sin
cos
1



n
nn
nn
x
xx
xx

7. Example: Cont’
 As the method iterates,
the x sequences start
getting closer and
closer to the root
73908513.0
73908513.0
73911289.0
75036387.0
5
4
3
2




x
x
x
x

8. Example 1 Cont.
  423
1099331650 -
.+x.-xxf 
To aid in the understanding of how this
method works to find the root of an
equation, the graph of f(x) is shown to
the right,
where
Solution
Figure 4 Graph of the function f(x)

9. Example 1 Cont.
 
  x-xxf
.+x.-xxf -
33.03'
1099331650
2
423


Let us assume the initial guess of the root of is . This
is a reasonable guess (discuss why
and are not good choices) as the extreme values of the
depth x would be 0 and the diameter (0.11 m) of the ball.
  0xf m05.00 x
0x m11.0x
Solve for
 xf '

10. Example 1 Cont.
 
 
   
   
 
06242.0
01242.00.05
109
10118.1
0.05
05.033.005.03
10.993305.0165.005.0
05.0
'
3
4
2
423
0
0
01












xf
xf
xx
Iteration 1
The estimate of the root is

11. Advantages
Converges fast(quadratic
convergences),if it converges
Requires only one guess

12. Failure of the method to
converge to the root
It is important to review the proof of quadratic convergence of Newton's Method
before implementing it. Specifically, one should review the assumptions made in
the proof. For situations where the method fails to converge, it is because the
assumptions made in this proof are not met.
Overshoot
If the first derivative is not well behaved in the neighborhood of a particular root, the
method may overshoot, and diverge from that root.
Stationary point
If a stationary point of the function is encountered, the derivative is zero and the
method will terminate due to division by zero.
Poor initial estimate
A large error in the initial estimate can contribute to non-convergence of the
algorithm.
Mitigation of non-convergence
In a robust implementation of Newton's method, it is common to place limits on the
number of iterations, bound the solution to an interval known to contain the root,
and combine the method with a more robust root finding method.

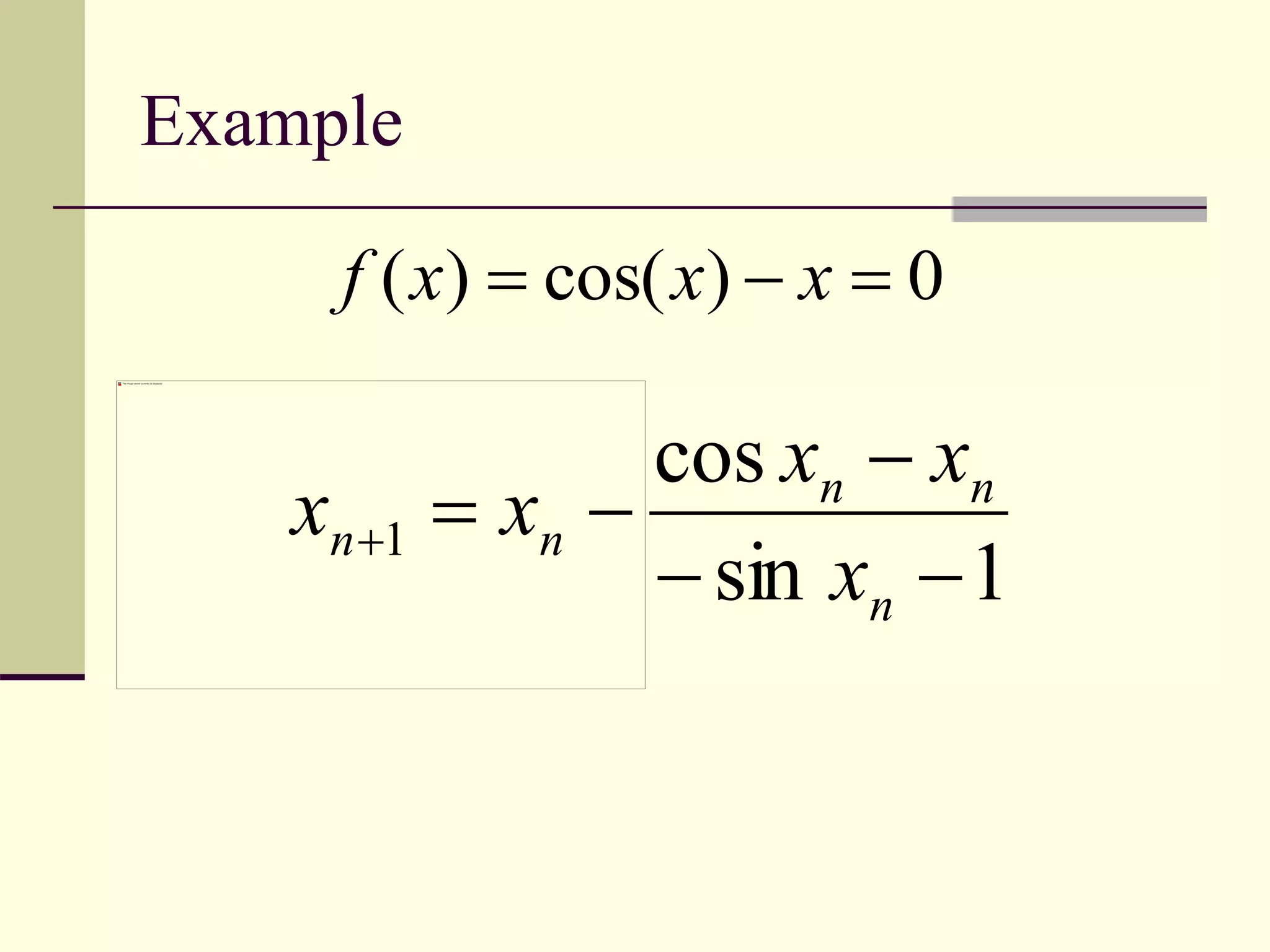
13. Slow convergence for roots of multiplicity > 1
If the root being sought has multiplicity greater than one, the
convergence rate is merely linear (errors reduced by a
constant factor at each step) unless special steps are taken.
When there are two or more roots that are close together
then it may take many iterations before the iterates get close
enough to one of them for the quadratic convergence to be
apparent. However, if the multiplicity m of the root is known,
one can use the following modified algorithm that preserves
the quadratic convergence rate:
[1]

14. Summary
 The Newton-Raphson method is an
alternative to solve roots for equations
 It uses a correction factor
 Used in computer programs today to solve
extremely complicated equations

15. Reference
 Calculus, Fourth Edition, James Steward,
 The New Turing Omnibus, AK Dewdney,
 www.wikepidia.com