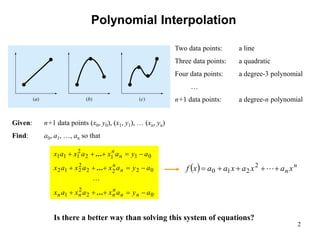
This document discusses various methods for polynomial interpolation of data points, including Newton's divided difference interpolating polynomials and Lagrange interpolation polynomials. It provides formulas and examples for linear, quadratic, and general polynomial interpolation using Newton's method. It also covers an example of using multiple linear regression with log-transformed data to develop a model relating fluid flow through a pipe to the pipe's diameter and slope.

1. 1
Interpolation

2. 2
Polynomial Interpolation
Given: n+1 data points (x0, y0), (x1, y1), … (xn, yn)
Find: a0, a1, …, an so that
Two data points: a line
Three data points: a quadratic
Four data points: a degree-3 polynomial
…
n+1 data points: a degree-n polynomial
  n
n x
a
x
a
x
a
a
x
f 



 
2
2
1
0
0
2
2
1
0
2
2
2
2
2
1
2
0
1
1
2
2
1
1
1
a
y
a
x
a
x
a
x
a
y
a
x
a
x
a
x
a
y
a
x
a
x
a
x
n
n
n
n
n
n
n
n
n
n















...
...
...

Is there a better way than solving this system of equations?

3. 3
Newton’s Divided-Difference Interpolating Polynomials
Linear Interpolation
Connecting two data points with a straight line
f1(x) designates a first-order interpolating
polynomial.
)
(
)
(
)
(
)
(
0
1
0
1
0
0
1
x
x
x
f
x
f
x
x
x
f
x
f





Linear-interpolation
formula
Slope
)
(
)
(
)
(
)
(
)
( 0
0
1
0
1
0
1 x
x
x
x
x
f
x
f
x
f
x
f 





4. 4
Linear Interpolation
   
   
 
0
0
1
0
1
0
1 x
x
x
x
x
f
x
f
x
f
x
f 




Given: two points (x0, y0), (x1, y1)
Find: a line that goes through the two points.
Example: f(x) = ln x
x0 = 1 and x1 = 6:
f1(2) = 0.3583519
x0 = 1 and x1 = 4
f1(2) = 0.4620981
ln 2 = 0.6931472
The closer the interval the better interpolation result!

5. 5
   
   
 
0
0
1
0
1
0
1 x
x
x
x
x
f
x
f
x
f
x
f 





6. 6

7. 7

8. 8
Quadratic Interpolation
 
   
       
0
2
0
1
0
1
1
2
1
2
2
0
1
0
1
1
0
0
x
x
x
x
x
f
x
f
x
x
x
f
x
f
b
x
x
x
f
x
f
b
x
f
b











      
1
0
2
0
1
0
2 x
x
x
x
b
x
x
b
b
x
f 





Given: three points (x0, y0), (x1, y1), (x2,y2)
Find: a quadratic f2(x) = a0 + a1x + a2x2 that goes through the three points.
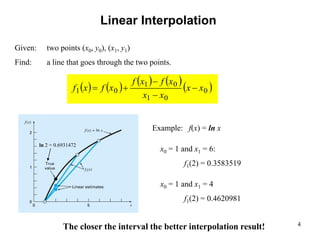
Example: f(x) = ln x
Data points:
b0 = 0
b1 = (1.386294 – 0)/(4 – 1) = 0.4620981
b2 = [(1.791759 – 1.386294)/(6-4) – 0.4620981]/(6-1)
= -0.0518731
f2(2) = 0.5658444
ln 2 = 0.6931472

9. 9
General Newton’s Interpolation Polynomial
 
 
 
0
1
1
0
1
1
0
0
x
x
x
x
f
b
x
x
f
b
x
f
b
n
n
n ,
,
,
,






           
1
1
0
1
0
2
0
1
0 










 n
n
n x
x
x
x
x
x
b
x
x
x
x
b
x
x
b
b
x
f 
...
     
j
i
j
i
j
i
x
x
x
f
x
f
x
x
f



,
Given: n+1 points (x0, y0), (x1, y1), …, (xn, yn) (yi = f(xi), i=0,1,…,n)
Find: fn(x) = a0 + a1x + a2x2 + … + anxn that goes through the n+1 points.
where
     
k
i
k
j
j
i
k
j
i
x
x
x
x
f
x
x
f
x
x
x
f



,
,
,
,
     
0
0
2
1
1
1
0
1
1
x
x
x
x
x
f
x
x
x
f
x
x
x
x
f
n
n
n
n
n
n
n


 



,
,
,
,
,
,
,
Bracket function, the first divide difference
between the values of f(X1) and f(X0)
Divided
difference
polynomial

10. 10
Example of Newton’s Interpolation Polynomial
Given: (1, 0), (4, 1.386294), (6, 1.791759), (5, 1.609438) (of function ln x)
Find: estimate ln 2 with a third-order Newton’s interpolation
= b1
= b0 = b1 = b2 = b3
= b2
= b3

11. 11
Example of Newton’s Interpolation Polynomial
x0
x1
x3
x2

12. 12

13. 13

14. 14
Lagrange Interpolation Polynomials
where
Product

15. 15

16. 16

17. 17
Miscellaneous problems #1

18. 18

19. 19
Miscellaneous problems #2

20. 20

21. 21
Miscellaneous problems #3

22. 22

23. 23

24. 24
A mechanical engineering study indicates that fluid flow through a pipe is
related to pipe diameter and slope (by the data as given below).
Suppose it is already known that Q, S, and D are related by the power relation
Use log-transformation + multiple linear regression to analyze this data. Then use the
resulting model to predict the flow for a pipe with a diameter of 2.5 ft and slope of 0.025 ft/ft.
2
1
a
a
0 S
D
a
Q 
Miscellaneous problems #4

25. 25
The laws of logarithms

26. 26
Multiple Linear Regression
Given: n points 3D (y1, x11, x12) (y2, x12, x22), …, (yn, x1n, x2n)
Find: a plane y = a0 + a1x1 + a2x2 that minimizes

27. 27
Analysis of Experimental Data
2
2
1
1 z
a
z
a
loga
y 0 


    /s
ft
0.025
2.5
55.9
Q 3
0.54
2.62
1
84.


y = log Q, z1 = log D, z2 = log S
Multi-linear regression on y – (z1, z2)

28. 28
Special Problem 6

29. 29
Homework
1-
2-
3-

30. 30
4-
5-