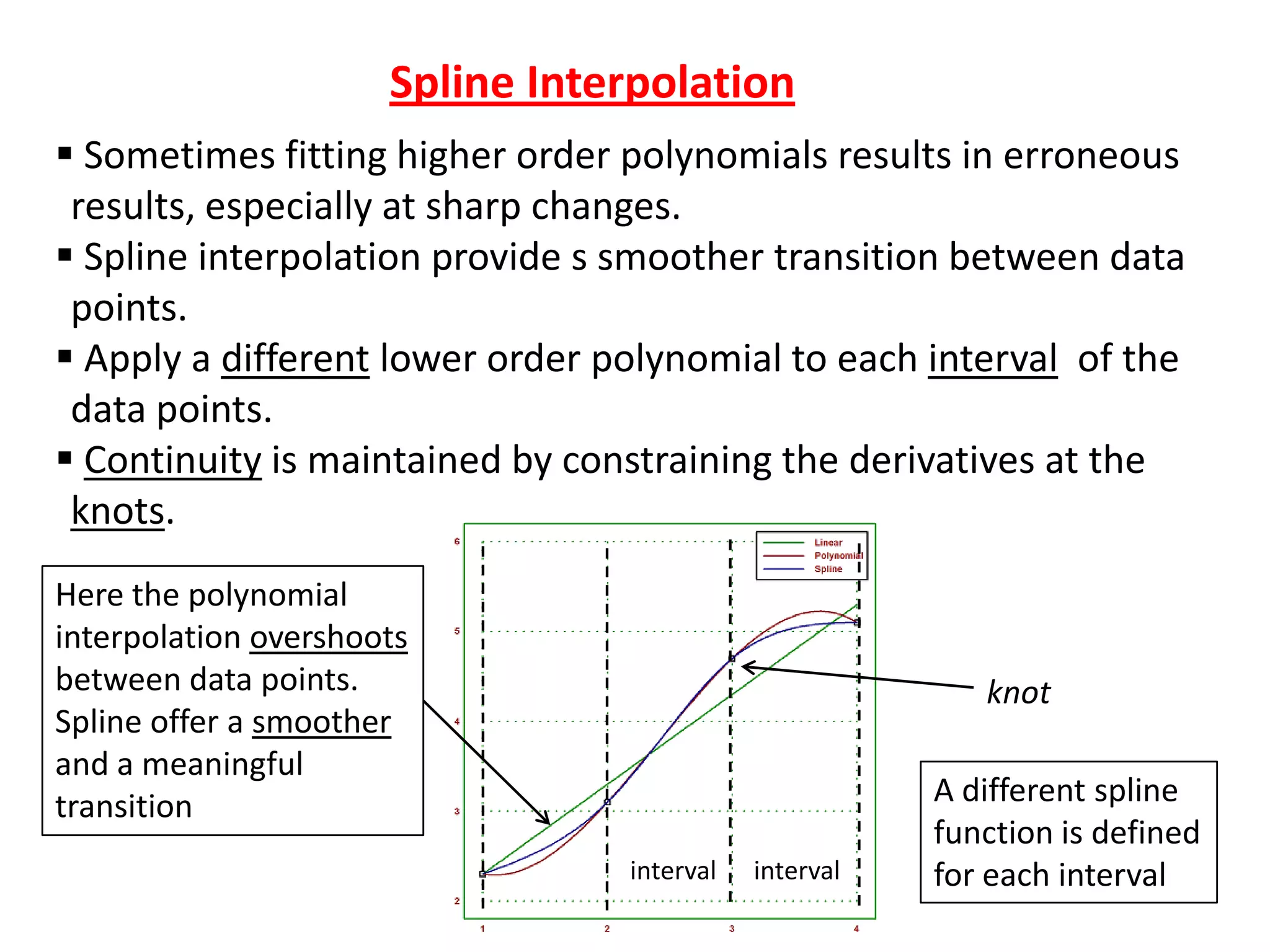
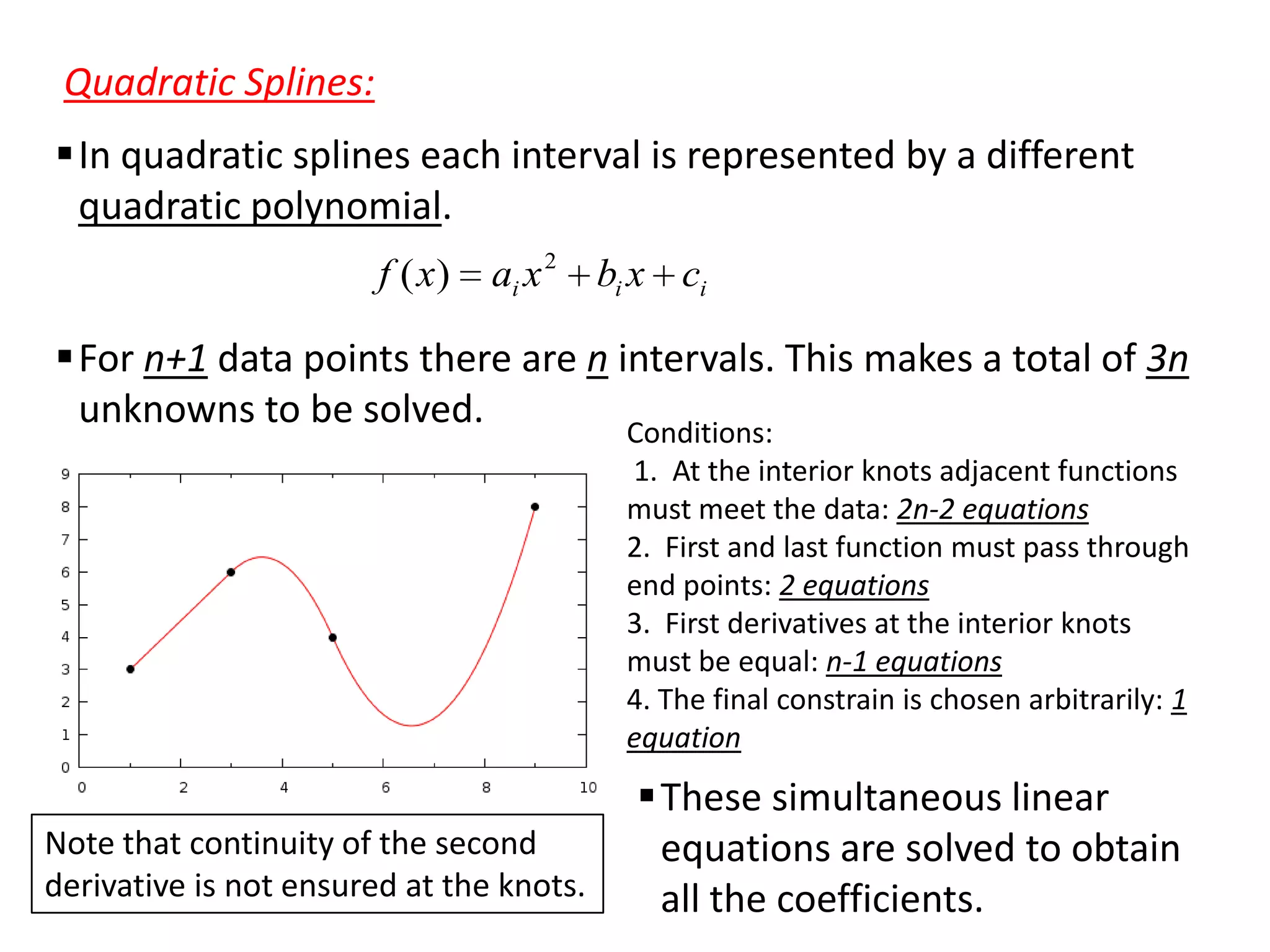
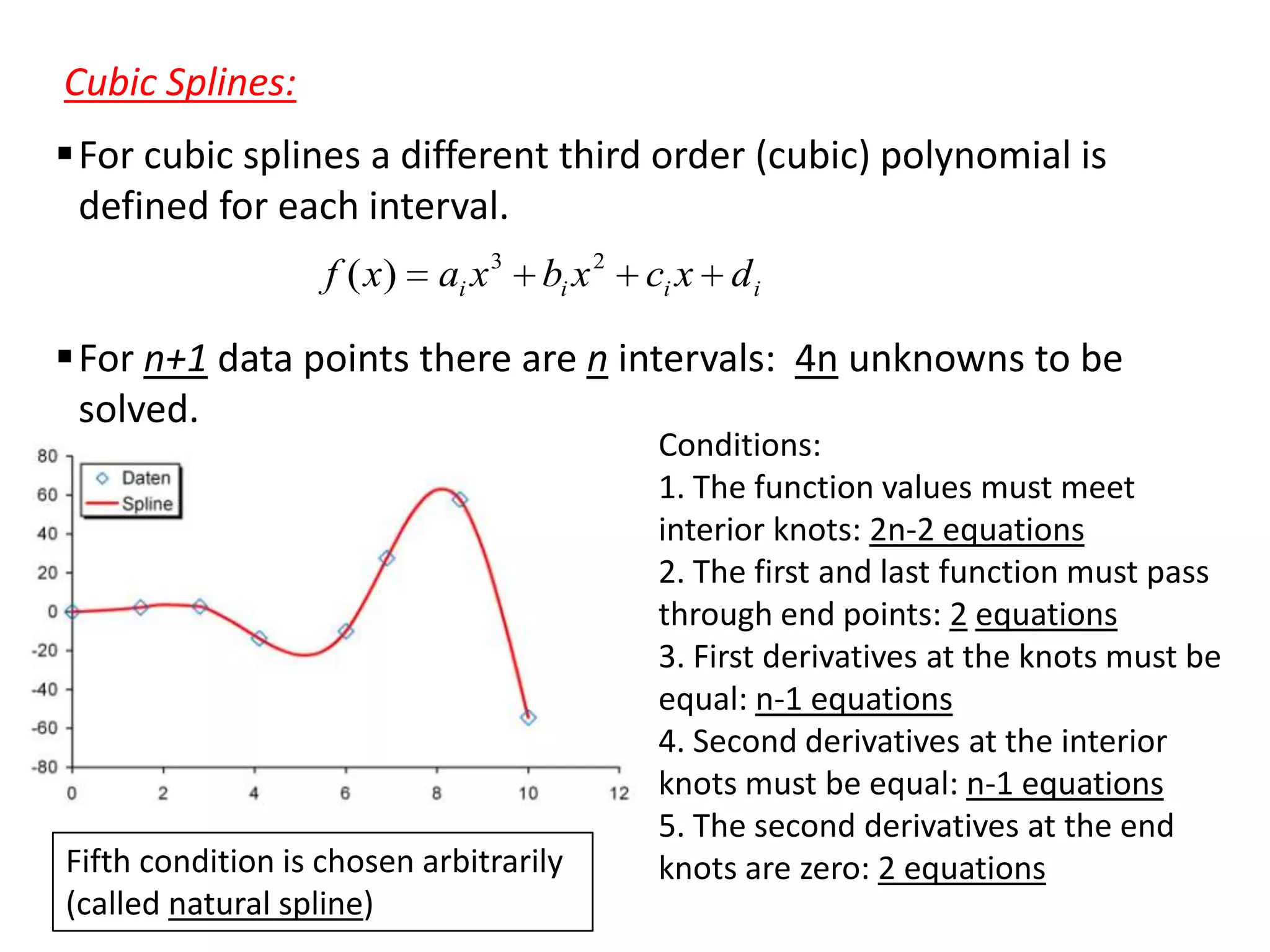
This document discusses various interpolation methods: - Newton's divided differences method uses finite differences to determine polynomial coefficients that fit scattered data points. Lagrange polynomials provide an alternative formulation. - Spline interpolation smooths transitions by fitting different lower order polynomials to intervals between data points, maintaining continuity of derivatives at knots. - Inverse interpolation finds the independent variable value corresponding to a given dependent variable value, using normal interpolation and root finding.

1. Part 5b:
INTERPOLATION
–
–
–
–
Newton’s Divided-Differences
Lagrange Polynomial Interpolation
Inverse Interpolation
Spline Interpolation

2. Introduction:
 Interpolation is the process of estimating intermediate values
between precisely defined data points.
For n+1 scattered data points there is a unique n-th order
polynomial fit function.
n+1=2
n+1=3
n+1=4
 Polynomial interpolation is the process of determining the unique
nth-order polynomial that fits (n+1) data points.
One can define the n-th order polynomial in different formats, e.g.,
Newton polynomials
These formats are well-suited for
computational implementations
Lagrange polynomials

3. Newton’s Divided Differences
 One of the most popular interpolating functions
Linear interpolation:
 Simplest form of interpolation: connect two data points by a
underlying
straight line, and estimate the intermediate value.
f(x)
f1(x) fit function
Similarity of the triangles:
f1 ( x) f ( x0 )
x x0
f(x1)
f1(x)
f(x0)
f ( x1 ) f ( x0 )
x1 x0
finite divided difference
of first derivative
x0
x
x1
f1 ( x)
f ( x0 )
f ( x1 ) f ( x0 )
( x x0 )
x1 x0
for data points
f1 ( xi )
function
f ( xi )
represents the first
order interpolation
linear interpolation formula

4. Quadratic interpolation:
 If you have three data points, you can introduce some curvature
for a better fitting.
 A second-order polynomial (quadratic polynomial) of the form
f 2 ( x) b0 b1 ( x x0 ) b2 ( x x0 )( x x1 )
To determine the values of the coefficients;
x
x
x
x0
x1
x2
b0
f ( x0 )
b1
f ( x1 ) f ( x0 )
x1 x0
b2
If you expand the
terms, this is nothing
different a general
polynomial
Linear
interpolation
formula
f ( x2 ) f ( x1 ) f ( x1 ) f ( x0 )
x2 x1
x1 x0
( x2 x0 )
Quadratic
interpolation
formula
finite divided
difference of
second derivative

5. General form of Newton’s interpolating polynomials:
In general, to fit an n-the order Newton’s polynomial to (n+1) data
points:
f n ( x) b0 b1 ( x x0 ) b2 ( x x0 )( x x1 ) .. bn ( x x0 )( x x1 )..( x xn 1 )
where the coefficients:
b0
f [ x0 ]
b1
f [ x1 , x0 ]
b2
f [ x2 , x1 , x0 ]
data points
n-th finite divided difference:
…
bn
brackets represent the
function evaluations for
finite divided-differences
f [ xn , xn 1 ,.., x1 , x0 ]
f [ xn , xn 1 ,.., x1 , x0 ]
f [ xn , xn 1 ,.., x1 ] f [ xn 1 ,.., x1 , x0 ]
( xn x0 )

6.  These differences can be evaluated for the coefficients and
substituted into the fitting function.
f n ( x)
f ( x0 ) ( x x0 ) f [ x1 , x0 ] ( x x0 )(x x1 ) f [ x2 , x1 , x0 ]
.. ( x x0 )(x x1 )..(x xn 1 ) f [ xn , xn 1 ,.., x0 ]
 x values are not need to be equally
spaced.
 x values are not necessarily in order.
Newton’s divideddifference interpolating
polynomial

7. Error for Newton’s interpolating polynomials:
 Newton’s divided difference formula is similar to Taylor
expansion formula, adding higher order derivatives of the
underlying function.
 A truncation error can be defined as in the case of Taylor series
approximation:
Rn
f ( n 1) ( )
( x x0 )( x x1 )..( x xn )
(n 1)!
where is somewhere in the
interval containing the unknown
and the data.
For Taylor series
approximation error
Rn
f ( n 1) ( )
( xi
(n 1)!
1
xi ) n
Above formulation requires prior knowledge of the underlying
function and its derivative, so cannot be evaluated.
1

8. An alternative formulation that does not require prior knowledge
of the underlying function:
Rn
f [ x, xn , xn 1 ,..., x0 ]( x x0 )( x x1 )..( x xn )
(n+1)th finite
divided difference
 One more data point (xn+1) is needed to evaluate the equation.
Rn
f [ xn 1 , xn , xn 1 ,..., x0 ]( x x0 )( x x1 )..( x xn )
This relationship is equivalent to
Rn
f n 1 ( x)
f n 1 ( x)
f n ( x)
f n ( x) Rn
(next estimate) - (current estimate)
increment added to the (n)th order case
to calculate (n+1)th order case is equal to
the error for the n-th order case.

9. Lagrange Polynomial Interpolation
A Lagrange polynomial can be stated concisely as
f n ( x)
Li ( x) f ( xi )
Li ( x)
j 0
j i
i 0
For example:
n 1
n
2
x xj
n
n
x x0
f ( x1 )
x1 x0
xi
xj
In fact, Lagrange
polynomials is just a
different formulation of
Newton’s polynomials
f1 ( x)
x x1
f ( x0 )
x0 x1
f1 ( x)
( x x0 )(x x2 )
( x x1 )(x x2 )
f ( x0 )
f ( x1 )
( x0 x1 )(x0 x2 )
( x1 x0 )(x1 x2 )
( x x0 )(x x1 )
f ( x2 )
( x2 x0 )(x2 x1 )

10.  In the formula, each term Li (x) will be equal to 1 for x=xi , and
zero for all other data points.
 Thus, each product Li (x) fi(x) takes on the value of fi(x) at the
data point.

11. Error is defined same as before
Rn
f [ x, xn , xn 1 ,..., x0 ]( x x0 )( x x1 )..( x xn )
(An additional point (xn+1) is needed for evaluation)
In summary:
Newton’s method is preferable for exploratory computations (n
is not known a priori).
> Newton method has advantages because of the insight for the
behavior between different orders (consider Taylor series).
> Error estimate in Newton method can easily be implemented
as it employs a finite difference.
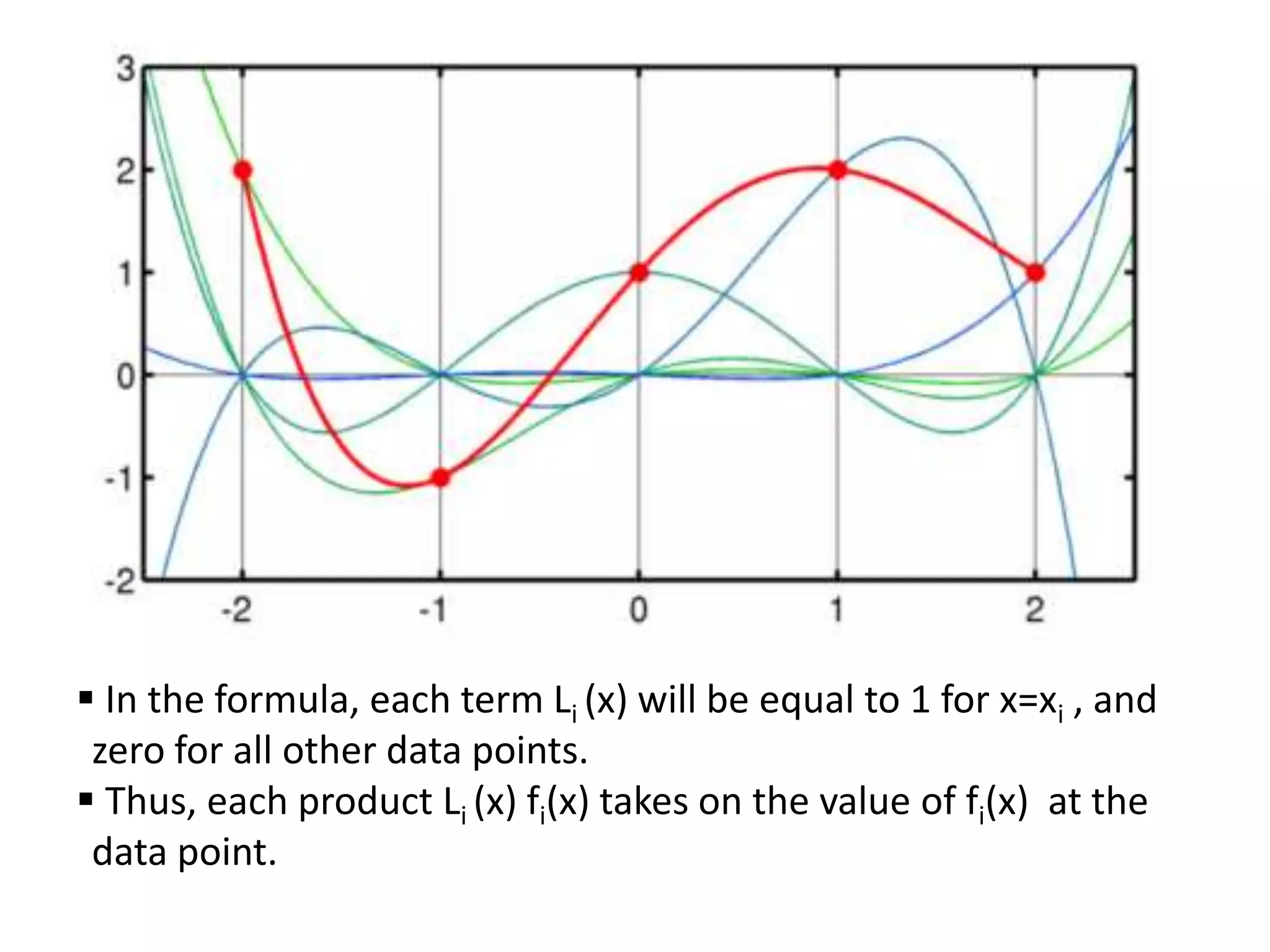
Lagrange method is preferable when only one interpolation is
performed (order n is known a priori),
> It is easier for computational implementation.

12. Polynomial coefficients:
 Newton and Lagrange methods do not provide the coefficients
of the conventional form
f ( x)
a0
a1 x a2 x 2 ... an x n
 With (n+1) data points, all the (n+1) coefficients can be
determined by using elimination techniques. For example for
n=2:
2
f ( x)
a0
a1 x a2 x
satisfies the following linear equations
f ( x0 )
a0
a1 x0
2
a2 x0
f ( x1 )
a0
a1 x1
a2 x12
f ( x2 )
a0
a1 x2
2
a 2 x2
 The process is notoriously illconditioned and susceptible to round-off
errors:
keep the order (n) small.
use Lagrange or Newton interpolation.

13. Inverse Interpolation
dependant variable
independent variable
 Values of x are usually evenly spaced.
 Normally interpolation concerns finding an approximate f (x) for
a given intermediate value of x.
 What if reverse is needed, that is value of f(x) is given and need
to find the corresponding x value (inverse interpolation).
 Two possible solutions:
Switch x by f(x) and apply Lagrange/Newton interpolation.
(this method is not suitable because there is no guarantee that
the new abscissa values will be evenly distributed,-in fact,
usually highly uneven.)
Apply normal interpolation, and find the x value that satisfies
the given f(x) value
a root finding problem.
f (x)
x

14. Equally spaced data:
 Newton/Lagrange methods are compatible for arbitrarily spaced
data
 Before the computer era, equally spaced data had to be
used, but computer implementation of these methods do not
require it anymore.
 Evenly spaced data is required for other applications
too, e.g., numerical differentiation and integration.
Extrapolation:
 The process of f(x) for a point outside of
the range of x values.
 If the extrapolated x value is not near
the evaluation points, the error can be
very large. So, extreme caution is
fit curve
required during extrapolation.
true curve
extrapolation

15. Spline Interpolation
 Sometimes fitting higher order polynomials results in erroneous
results, especially at sharp changes.
 Spline interpolation provide s smoother transition between data
points.
 Apply a different lower order polynomial to each interval of the
data points.
 Continuity is maintained by constraining the derivatives at the
knots.
Here the polynomial
interpolation overshoots
between data points.
Spline offer a smoother
and a meaningful
transition
knot
interval
interval
A different spline
function is defined
for each interval

16. Linear Splines:
 Each interval is connected by a straight line.
For each interval
f ( x)
f ( xi ) mi ( x xi )
where mi
f ( xi 1 ) f ( xi )
( xi 1 xi )
 Linear splines is identical to the first order polynomial fit.
 Linear spline function is discontinuous at the knots. So, we need
to use higher order polynomials to maintain continuity.
 In general, for m-th derivative to be continuous, an order (m+1)
spline fit must be used.

17. Quadratic Splines:
In quadratic splines each interval is represented by a different
quadratic polynomial.
f ( x)
ai x 2
bi x ci
For n+1 data points there are n intervals. This makes a total of 3n
unknowns to be solved.
Conditions:
1. At the interior knots adjacent functions
must meet the data: 2n-2 equations
2. First and last function must pass through
end points: 2 equations
3. First derivatives at the interior knots
must be equal: n-1 equations
4. The final constrain is chosen arbitrarily: 1
equation
Note that continuity of the second
derivative is not ensured at the knots.
These simultaneous linear
equations are solved to obtain
all the coefficients.

18. Cubic Splines:
For cubic splines a different third order (cubic) polynomial is
defined for each interval.
f ( x)
ai x 3 bi x 2
ci x d i
For n+1 data points there are n intervals: 4n unknowns to be
solved.
Fifth condition is chosen arbitrarily
(called natural spline)
Conditions:
1. The function values must meet
interior knots: 2n-2 equations
2. The first and last function must pass
through end points: 2 equations
3. First derivatives at the knots must be
equal: n-1 equations
4. Second derivatives at the interior
knots must be equal: n-1 equations
5. The second derivatives at the end
knots are zero: 2 equations