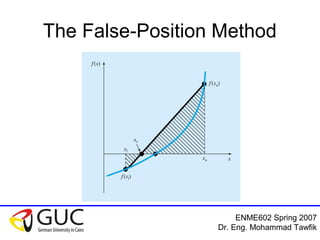
The document discusses numerical analysis techniques, specifically bracketing methods for finding roots of nonlinear equations. It explains the bisection and false-position methods, outlining algorithms and the necessity of termination criteria to prevent infinite loops. Additionally, the document emphasizes the importance of bracketing techniques for solving continuous functions when solutions exist.

1. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Roots of Nonlinear Equations

2. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Objectives
• Understand the need for numerical solutions of
nonlinear equations
• Be able to use the bisection algorithm to find a
root of an equation
• Be able to use the false position method to find a
root of an equations
• Write down an algorithm to outline the method
being used
• Realize the need for termination criteria

3. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Root of Nonlinear Equations
• Solve   0xf

4. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Bracketing Methods

5. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Intermediate Value Theorem
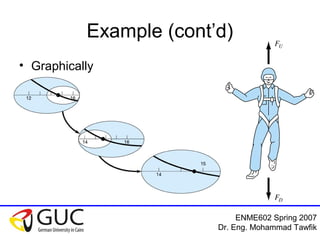
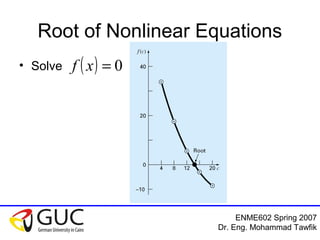
• For our specific interest
If f(x) is continuous in the interval [a,b], and
f(a).f(b)<0, then there exists ‘c’ such that
a<c<b and f(c)=0.

6. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Example
• For the parachutist problem
   mct
e
c
mg
tv /
1 

• Find ‘c’ such that   smv /4010 
• Where, kgmsmg 1.68,/8.9 2


7. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Example (cont’d)
• You get  1.68/10
1
8.9*1.68
40 c
e
c


• OR:
• Giving,
    401
38.667 147.0
  c
e
c
cf
    269.216&067.612  ff

8. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Example (cont’d)
• Graphically

9. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
The Bisection Method

10. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Algorithm
1. Search for a & b such that
f(a).f(b)<0
2. Calculate ‘c’ where c=0.5(a+b)
3. If f(c)=0; end
4. If f(a).f(c)>0 then let a=c; goto step 2
5. If f(b).f(c)>0 then let b=c; goto step 2

11. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Algorithm (cont’d)
• That algorithm will go on forever!
• We need to define a termination
criterion
• Examples of termination criteria:
1. |f(c)|<es
2. |b-a|<es
3. ea=|(cnew -cold)/cnew|<es
4. Number of iterations > N

12. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Algorithm: Modified
• So, let’s modify the algorithm
1. Search for a & b such that
f(a).f(b)<0
2. Calculate ‘c’ where c=0.5(a+b)
3. If |f(c)|<es; end
4. If f(a).f(c)>0 then let a=c; goto step 2
5. If f(b).f(c)>0 then let b=c; goto step 2

13. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
False-Position Method

14. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
The False-Position Method

15. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Evaluating ‘c’
• The slope of the line
joining the two point
maybe written as:
bc
yy
mor
ac
yy
m bcac






bc
yy
ac
yy bcac





     bcac yyacyybc 

16. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Evaluating ‘c’
     ba yacybc  00
aybycycy baab 
 ab
ab
yy
byay
c



   
   afbf
bafabf
c




17. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
False Position Algorithm
1. Search for a & b such that
f(a).f(b)<0
2. Calculate ‘c’ where
c=(af(b)-bf(a))/(f(b)-f(a))
3. If |f(c)|<es; end
4. If f(a).f(c)>0 then let a=c; goto step 2
5. If f(b).f(c)>0 then let b=c; goto step 2

18. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Conclusion
• The need for numerical solution of nonlinear
equations led to the invention of approximate
techniques!
• The bracketing techniques ensure that you will
find a solution for a continuous function if the
solution exists
• A termination criterion should be embedded into
the numerical algorithm to ensure its
termination!

19. Numerical Analysis: Bracketing Methods
Mohammad Tawfik
#WikiCourses
http://WikiCourses.WikiSpaces.com
Homework #1
• Chapter 5, page 139, numbers:
5.3,5.6,5.7,5.8,5.12
• You are not required to get the solution
graphically!
• Homework due Next week!