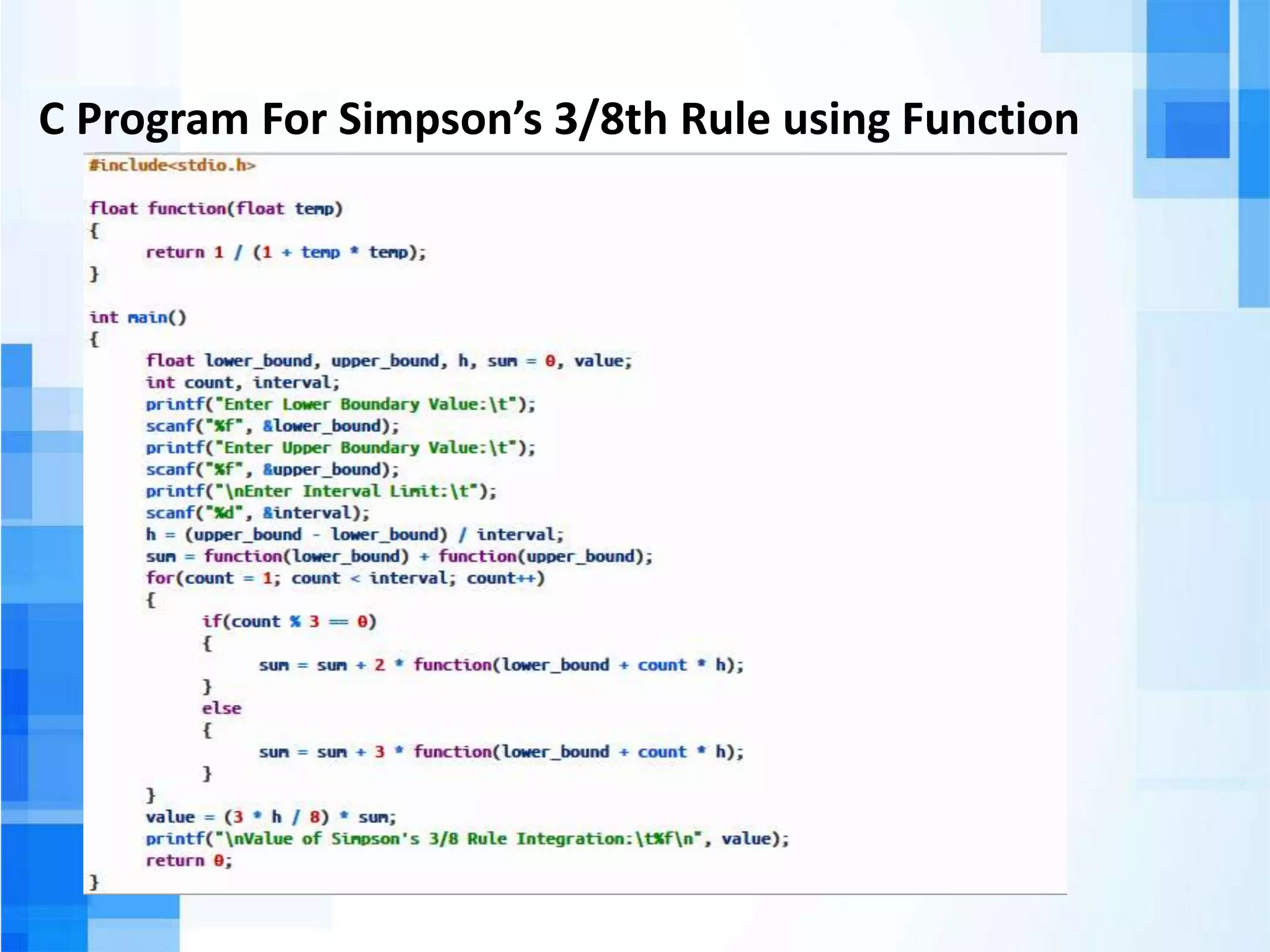
The document is a presentation on Simpson's 3/8 rule. It introduces numerical integration and Simpson's rule as an improvement over the midpoint and trapezium rules. It explains that Simpson's rule has two variations: Simpson's 1/3 rule and Simpson's 3/8 rule. Simpson's 3/8 rule is based on a cubic interpolation and is also known as Simpson's 2nd rule, using a polynomial of degree 3. It provides an example C program for implementing Simpson's 3/8 rule when the number of strips is a multiple of three.

1. Presentation
On
Simpson’s 3/8 rule
Presented By:
Pratiksha Sharma
B.C.A. 2nd Year

2. Content:-
 Simpson’s Rule
 SIMPSON’S 3/8 RULE
 Example
C Program For Simpson’s 3/8th Rule
using Function

3. Numerical integration
• Numerical integration is used to calculate a
numerical approximation for the value S the area
under the curve defined by f(x)}.

4. Simpson’s Rule
• The midpoint rule was first improved upon by the
trapezium rule.
• A further improvement is the Simpson's rule.
• Instead of approximating the curve by a straight line,
we approximate it by a quadratic or cubic function.

5. Simpson’s Rule
• There are two variations of the rule:
• Simpson’s 1/3 rule and
• Simpson’s 3/8 rule.

6. SIMPSON’S 3/8 RULE
Simpson's 3/8 rule is another method for numerical
integration proposed by Thomas Simpson. It is based
upon a cubic interpolation rather than a quadratic
interpolation.
 It is also known as Simpson's 2nd rule.
• In this rule, y(x) is a polynomial of degree 3.
• If the number of strips is divisible by three we can
use the 3/8 rule.

7. SIMPSON’S 𝟑/𝟖
RULE(USE WHEN N=MULTIPLE OF THREE )

9. C Program For Simpson’s 3/8th Rule using Function

10. Output