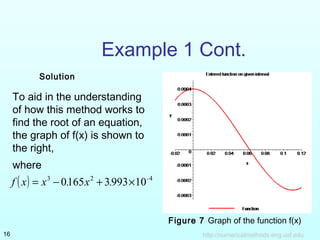
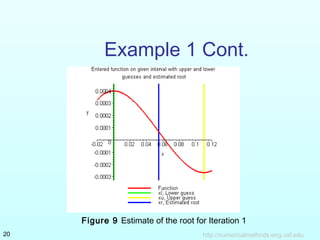
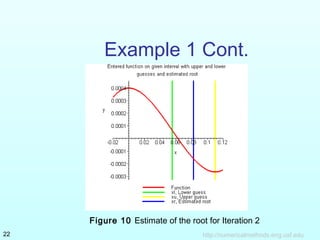
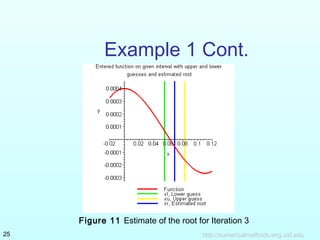
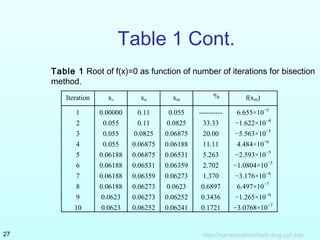
The document describes the bisection method for finding the root of an equation. It provides the theoretical basis and algorithm for the bisection method. An example problem is worked through over 3 iterations to demonstrate how the method converges on a root by narrowing the range between the lower and upper bounds. The example tracks the estimate of the root and absolute relative error at each step. Advantages and drawbacks of the bisection method are also summarized.