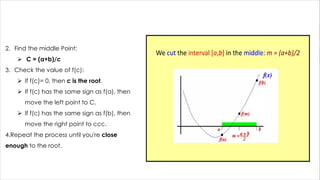
The bisection method is a step-by-step way to find where a function crosses zero (its "root"). It works by narrowing down a range where the root must be, cutting that range in half each time until it's precise enough. How It Works: Pick two starting points where the function has opposite signs (one positive, one negative). Find the midpoint between them and check its value. Replace either the left or right point with this midpoint, keeping the sign change. Repeat this halving process until the range is as small as you need. Key Points: Always works for continuous functions that change sign. Simple and reliable, but not the fastest method. Doesn't need complex calculations, just basic evaluations. Example: Used in engineering and science to solve equations when exact solutions are hard to find. A go-to method when you need a dependable way to find roots!

1. Bisection Method
Khuda Bux (CSC-23F-259)
Abid Ali (CSC-22F-021)
Zeeshan Owais (CSC-22F-164)
Numerical Method for Root Finding
Course: Numerical Computing
Instructor: Mrs.Naila Rozi
Section 5-A

2. Introduction
1. What is the Bisection Method?
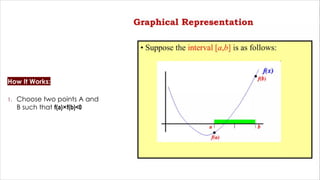
• It is a numerical method used to find the root of a mathematical function.
• A root is the value of x that makes the function f(x)=0.
• The method works by repeatedly dividing an interval in half and checking where the root lies.
• The Bisection Method works only if the function is continuous (no breaks or jumps).
Ø It needs two starting points: [A] and [B], where:
• f(a) is negative, and
• f(b) is positive
• This means the root lies between [A] and [B].

3. How It Works:
1. Choose two points A and
B such that f(a)×f(b)<0

4. 2. Find the middle Point:
Ø C = (a+b)/c
3. Check the value of f(c):
Ø If f(c)= 0, then c is the root.
Ø If f(c) has the same sign as f(a), then
move the left point to C.
Ø If f(c) has the same sign as f(b), then
move the right point to ccc.
4.Repeat the process until you're close
enough to the root.

5. Historical Background
 Early Origins:
• The idea of finding roots by narrowing down intervals has been
around for centuries.
• Ancient mathematicians used logical thinking to estimate
solutions, even before calculators or computers existed.

6. Historical Background
 Key Contributors:
1. Bernard Bolzano (1781–1848) – Czech mathematician
Ø Introduced the Intermediate Value Theorem, which is the
foundation of the Bisection Method.
Ø He proved that if a continuous function changes sign,
there must be a root between the two points.
2. Augustin-Louis Cauchy (1789–1857) – French
mathematician
Ø Formalized the method in his work on numerical analysis.
Ø Cauchy helped define how the method could be used
step by step in solving real problems.

7. Historical Background
 Formalization and Usage:
• The term "Bisection Method" became popular in the
19th and 20th centuries, as numerical methods were
developed for use with computers.
• It was one of the first algorithms taught in numerical
methods courses due to its simplicity and reliability.

8. Algorithm of the Bisection Method
 Pseudocode
Input: f(x), a, b, ε
If f(a) * f(b) ≥ 0:
Print "Invalid interval" and exit
Repeat:
c = (a + b) / 2
If f(c) == 0 or (b - a)/2 < ε:
Return c as root
Else If f(a) * f(c) < 0:
b = c
Else:
a = c
Until root is found

9. Example

10. Conclusion
• The Bisection Method is one of the simplest and most reliable numerical techniques to find the root of a nonlinear
equation.
• It works by repeatedly narrowing down an interval where a root exists, using the idea that the function must change
signs across a root.
• Although the method can be slow, it is guaranteed to converge if the function is continuous and the initial interval is
chosen correctly.
• The method does not require derivatives, making it useful for solving problems where the derivative is hard to find.
• Overall, the Bisection Method is a foundational tool in numerical analysis, widely used in science, engineering, and
computer science for root-finding problems.

11. Thanks