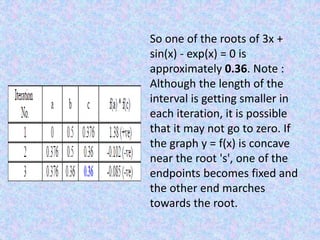
The False-Position Method is an iterative root-finding algorithm that improves upon the bisection method. It uses the slope of a line between two points to estimate a new root, rather than always bisecting the interval. Given an initial interval where the function changes sign, it calculates a new x-value at the intersection of the x-axis and a line through two existing points. It then chooses a new interval based on where the function changes sign again. The method is similar to bisection but uses a different formula to calculate the new estimate. An example finds a root of 3x + sin(x) - exp(x) = 0 between 0 and 0.5, converging to a solution of approximately 0.

1. The False-Position Method

2. Introduction
The poor convergence of the bisection
method as well as its poor adaptability
to higher dimensions motivate the use
of better techniques. One such
method is the Method of False
Position.

3. Methodology
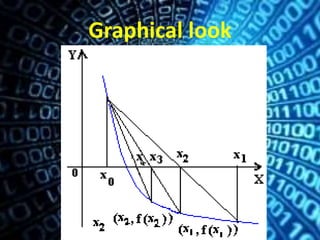
we start with an initial interval [x1,x2], and we
assume that the function changes sign only once
in this interval. Now we find an x3 in this
interval, which is given by the intersection of the
x axis and the straight line passing through
(x1,f(x1)) and (x2,f(x2)). It is easy to verify that
x3 is given by

4. Methodology
Now, we choose the new
interval from the two choices
[x1,x3] or [x3,x2] depending on in
which interval the function
changes sign.

5. Note
The False-Position and Bisection
algorithms are
quite similar. The only difference is
the formula used to
calculate the new estimate of the
root x3

6. Graphical look

7. Numerical Example
Find a root of 3x + sin(x) - exp(x) =0. The
graph of this equation is given in the
figure.
From this it's clear that there is a
root between 0
and 0.5 and also
another root between 1.5 and
2.0. Now let us consider the function f
(x) in the
interval [0, 0.5] where f (0) * f (0.5) is
less than
zero and use the regula-falsi scheme to
obtain the
zero of f (x) = 0.

8. So one of the roots of 3x +
sin(x) - exp(x) = 0 is
approximately 0.36. Note :
Although the length of the
interval is getting smaller in
each iteration, it is possible
that it may not go to zero. If
the graph y = f(x) is concave
near the root 's', one of the
endpoints becomes fixed and
the other end marches
towards the root.

9. Matlab implementation

10. Thank You…!

11. Presented by
Tayyaba Abbas
Roll no 5