The document provides an overview of numerical root-finding methods, focusing on the bisection and regula falsi (false position) methods. It includes discussions of algorithms, C program implementations, and examples demonstrating the application of these methods to find roots of equations. Key concepts such as linear and nonlinear equations, graphical representations, and classification of equations are also covered.

1. L.D. College of Engineering
Prepared By:
Divya Bhatia

2. Topics to be Covered
• Introduction of Bisection method
• Graphical Representation Of Bisection Method
• Finding Roots of Equations
• Classification of Equations
• Algorithm
• Flowchart
• C program
• Examples
• Introduction of Regula Falsi method
• Finding roots
• False Position formulae
• Algorithm
• C program
• Examples
• Merits Demerits
• Conclusion

3. Finding Roots of Equations
• In this topic we are examining equations with one
independent variable.
• These equations may be linear or non-linear
• Non-linear equations may be polynomials or
generally non-linear equations
• A root of the equation is simply a value of the
independent variable that satisfies the equation

4. Classification of Equations
• Linear: independent variable appears to the first
power only, either alone or multiplied by a
constant
• Nonlinear:
– Polynomial: independent variable appears
raised to powers of positive integers only
– General non-linear: all other equations

5. BISECTION METHOD
The bisection method in mathematics is a root-finding
method that repeatedly bisects an interval and then
selects a subinterval in which a root must lie for further
processing. It is a very simple and robust method, but it
is also relatively slow. Because of this, it is often used to
obtain a rough approximation to a solution which is then
used as a starting point for more rapidly converging
methods. The method is also called the interval halving
method.

6. Graphical Representation Of Bisection Method
.

7. Continue...
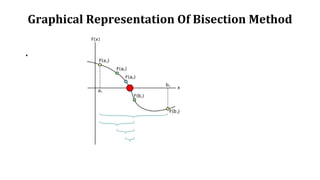
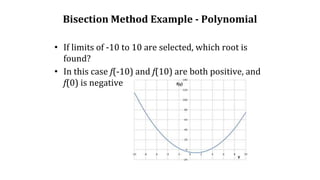
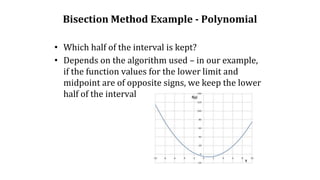
The method is applicable for numerically solving the
equation f(x) = 0 for the real variable x, where f is a
continuous function defined on an interval [a, b] and
where f(a) and f(b) have opposite signs. In this case a
and b are said to bracket a root since, by the
intermediate value theorem, the continuous function f
must have at least one root in the interval (a, b).

8. Algorithm
• 'Bisection Method
• 'Start loop
• Do While (abs(right - left) !=0.000)
• 'Calculate midpoint of domain
• midpoint = (right + left) / 2
• 'Find f(midpoint)
• If ((f(left) * f(midpoint)) < 0) Then
• 'Throw away right half

9. • right = midpoint
• Else If ((f(right) * f(midpoint)) < 0)
• 'Throw away left half
• left = midpoint
• Else
• 'Our midpoint is exactly on the root
• Exit Do
• End If
• Loop
• Return midpoint

10. Input lower and upper
limits low and high
Define tolerance tol
while high-low > 2*tol
mid = (high+low)/2
Evaluate function at
lower limit and
midpoint:
fl = f(low), fm = f(mid)
fl*fm > 0?
Keep upper half of
range:
low = mid
Keep lower half
of range:
high = mid
Display root (mid)
YESNO

11. C Program For Bisection Method
#include<stdio.h>
#include<conio.h>
# define eqn x*x-5
float f(float x)
{
float ans;
ans=eqn;
return(ans);}

12. Continue…
void main()
{
float a,b,x=0,x1=0;
int i=0;
printf("Enter the a and bn");
scanf("%f%f",&a,&b);
if(f(a)*f(b)>=0)
{
printf("The interval is wrongn");
getch();
return ;}

13. Continue...
do
{
x=(a+b)/2;
printf("ta=%f tb=%f tX%d=%f tf(x%d)=%fn",a,b,i,x,i,f(x));
if(x==x1)
{
printf("nnThe root is %fn",x);
break;
}
x1=x;

14. Continue...
i++;
if(f(a)*f(x)<0)
b=x;
else
a=x;
}while(f(a)-f(b)!=0.000);
printf("nThe final ans is %f",x);
getch();
}

15. Enter the a and b
2
2.5
a=2.000000 b=2.500000 X0=2.250000
f(x0)=0.062500
a=2.000000 b=2.250000 X1=2.125000
f(x1)=-0.484375
a=2.125000 b=2.250000 X2=2.187500
f(x2)=-0.214844
a=2.187500 b=2.250000 X3=2.218750
f(x3)=-0.077148
a=2.218750 b=2.250000 X4=2.234375
f(x4)=-0.007568
a=2.234375 b=2.250000 X5=2.242188
f(x5)=0.027405
a=2.234375 b=2.242188 X6=2.238281
f(x6)=0.009903
a=2.234375 b=2.238281 X7=2.236328
f(x7)=0.001163
Output of the Bisection Method

16. a=2.235962 b=2.236084 X12=2.236023
f(x8)=-0.000201
a=2.236023 b=2.236084 X13=2.236053
f(x9)=-0.000065
a=2.236053 b=2.236084 X14=2.236069
f(x10)=0.000003
a=2.236053 b=2.236069 X15=2.236061
f(x11)=-0.000031
a=2.236061 b=2.236069 X16=2.236065
f(x12)=-0.000014
a=2.236065 b=2.236069 X17=2.236067
f(x13)=-0.000005
a=2.236067 b=2.236069 X18=2.236068
f(x14)=-0.000001
a=2.236068 b=2.236069 X19=2.236068
f(x15)=0.000001
a=2.236068 b=2.236068 X20=2.236068
f(x16)=0.000000
The final ans is 2.236068
Continue…

17. Bisection Method Example - Polynomial
• Now consider this example:
• Use the bisection method, with allowed error of
0.0001

18. Bisection Method Example - Polynomial
• If limits of -10 to 0
are selected, the
solution converges
to x = -2

19. Bisection Method Example - Polynomial
• If limits of 0 to 10
are selected, the
solution converges
to x = 4

20. Bisection Method Example - Polynomial
• If limits of -10 to 10 are selected, which root is
found?
• In this case f(-10) and f(10) are both positive, and
f(0) is negative

21. Bisection Method Example - Polynomial
• Which half of the interval is kept?
• Depends on the algorithm used – in our example,
if the function values for the lower limit and
midpoint are of opposite signs, we keep the lower
half of the interval

22. Bisection Method Example - Polynomial
• Therefore, we converge to the negative root

23. Example 2
• Find the root of cos(x) - x * exp(x)
= 0
The graph of this equation is given
in the figure.
Let a = 0 and b = 1

24. .
Iteration
No.
a b c f(a) * f(c)
1 0 1 0.5 0.053 (+ve)
2 0.5 1 0.75 -0.046 (-ve)
3 0.5 0.75 0.625 -0.357 (-ve)
4 0.5 0.625 0.562 -7.52 * 10-3(-ve)
5 0.5 0.562 0.531 -2.168 * 10-3 (-ve)
6 0.5 0.531 0.516 3.648 * 10-4 (+ve)
7 0.516 0.531 0.524 -9.371 * 10-5(-ve)
8 0.516 0.524 0.520 -3.649 * 10-5(-ve)
9 0.516 0.520 0.518 -3.941 * 10-6(-ve)
10 0.516 0.518 0.517 1.229 * 10-5(+ve)

25. .
•So one of the roots of cos(x) - x *
exp(x) = 0 is approximately 0.517

26. Example 3
•Find the root of x - sin(x) - (1/2)=
0
• The graph of this equation is given
in the figure.
• Let a = 1 and b = 2

27. .Iteration
No.
a b c f(a) * f(c)
1 1 2 1.5 -8.554*10-4 (-ve)
2 1 1.5 1.25 0.068 (+ve)
3 1.25 1.5 1.375 0.021 (+ve)
4 1.375 1.5 1.437 5.679*10-3 (+ve)
5 1.437 1.5 1.469 1.42*10-3 (+ve)
6 1.469 1.5 1.485 3.042*10-4 (+ve)
7 1.485 1.5 1.493 5.023*10-5 (+ve)
8 1.493 1.5 1.497 2.947*10-6 (+ve)

28. .
•So one of the roots of x-sin(x)-(1/2)
= 0 is approximately 1.497.

29. FALSE POSITION
METHOD

30. Finding roots / solving equations
● The given quadratic formula provides a quick answer to all quadratic
equations:
● Easy
But, not easy
● No exact general solution (formula) exists for equations with
exponents greater than 4.

31. Finding roots…
● For this reason, we have to find out the root to solve
the equation.
● However we can say how accurate our solution is as
compared to the “exact” solution.
● One of the method is FALSE POSITION.

32. To refine the bisection method, we can choose a ‘false-position’ instead of
the midpoint.
The false-position is defined as the x position where a line connecting the
two boundary points crosses the axis.
The False-Position Method (Regula-Falsi)

33. Regula Falsi
• For example, if f(xlow) is much closer to zero than f(xup), it is
likely that the root is closer to xlow than to xup.
• False position method is an alternative approach where f(xlow)
and f(xup) are joined by a straight line; the intersection of
which with the x-axis represents and improved estimate of the
root.
• The intersection of this line with the x axis represents an
improved estimate of the root.

34. False Position formulae
● Using similar triangles, the intersection of the straight line with the x
axis can be estimated as
● This is the False Position formulae. The value of x then replaces
whichever of the two initial guesses, low x or up x , yields a function
value with the same sign as f (x) .

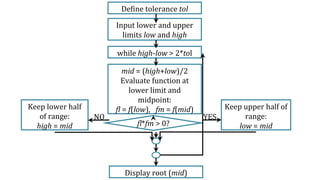
35. Regula Falsi Method Algorithm:
1.Start
2.Read values of x0, x1 and
*Here x0 and x1 are the two initial guesses
3.Computer function values f(x0) and f(x1)
4.Check whether the product of f(x0) and f(x1) is negative or not.
If it is positive take another initial guesses.
If it is negative then goto step 5.
5.Determine:
x = [x0*f(x1) – x1*f(x0)] / (f(x1) – f(x0))
6.Check whether the product of f(x1) and f(x) is negative or not.
If it is negative, then assign x0 = x;
If it is positive, assign x1 = x;
7.Check whether the value of f(x) is greater than 0.00001 or not.
If yes, goto step 5.
If no, goto step 8.
8.Display the root as x.
9.Stop

36. #include<stdio.h>
#include<conio.h>
# define eqn x*x-5
float f(float x)
{
float ans;
ans=eqn;
return(ans);
}
void main()
{
float a,b,x=0,x1=0;
int i=0;
printf("Enter the a and bn");
scanf("%f%f",&a,&b);
C Program For Regula Falsi

37. if(f(a)*f(b)>=0)
{
printf("The interval is wrongn");
getch();
return ;}
do
{
x=a-((b-a)/(f(b)-f(a)))*f(a);
printf("ta=%ftb=%ftX%d=%ftf(x%d)=%fn",a,b,i,x,i,f(x));
if(x==x1)
{
printf("nnThe root is %fn",x);
break;
}
Continue…

38. x1=x;
i++;
if(f(a)*f(x)<0)
b=x;
else
a=x;
}while(f(a)-f(b)!=0.000);
printf("nThe final ans is %f",x);
getch();
}
Continue…

39. Enter the a and b
2
2.5
a=2.000000 b=2.500000 X0=2.222222
f(x0)=-0.061728
a=2.222222 b=2.500000 X1=2.235294
f(x1)=-0.003460
a=2.235294 b=2.500000 X2=2.236025
f(x2)=-0.000193
a=2.236025 b=2.500000 X3=2.236066
f(x3)=-0.000010
a=2.236066 b=2.500000 X4=2.236068
f(x4)=-0.000001
a=2.236068 b=2.500000 X5=2.236068
f(x5)=0.000000
The final ans is 2.236068
Output of Regula Falsi Program

40. EXAMPLE
places.decimalthreecorrect to0.9and0.8betweenlies
which02)(equationofrootrealtheFind•  x
xexf

41. Solution
851.0
)2196.0(2136.0
)2196.0(9.02136.08.0
)()(
)()(
2136.0)9.0()(
2196.0)8.0()(
0.9and0.8betweenliesrootthat theknowWe
2
01
0110
2
1
0









x
xfxf
xfxxfx
x
fxf
fxf

42. Solution
900.0851.0
takeweNow
900.0xand0.851x
betweenless0f(x)ofroot
0)00697.0(2136.0)f(x)f(x
00697.0)851.0()(
10
12
21
2






xandx
The
Since
fxf

43. Solution
• Therefore, the root is 0.8526,corret to three decimal places.
85260
)00697.0(2136.0
)00697.0(900.02136.0851.0
)()(
)()(
3
01
0110
3
.x
xfxf
xfxxfx
x








44. EXAMPLE
places.decimalfourcorrect to
02.1logofrootrealtheCompute• 10 xx

45. Solution
.23136.0)f(x
,59794.0)0(,3xand2xTaking
3.and2betweenliesrootA
23136.02.143196.12.13log3)3(
59794.02.160206.02.12log2)2(
2.1)1(
2.1log)(
1
10
10
10
10







f
vef
vef
vef
xxxf

46. Solution
3.and2.72102betweenliesrootThe
01709.0)72102.2()f(x
72102.2
)59794.0(23136.0
)59794.0(323136.02
).......(....................
)()(
)()(
2
2
01
0110
2









vef
Now
x
i
xfxf
xfxxfx
x•.

47. Hence the root is 2.70465 correct to four decimal
places.
Solution
etc.2.74065x
,2.74064x
areionapproximatsuccessivetheprocess,this
72102.2
)59794.0(23136.0
)59794.0(323136.02
x
get,We
.(i),..........0.23136)f(xand01709.0)f(x
,3,72102.2xTaking
5
4
3
3
10
10








repeating
x
x

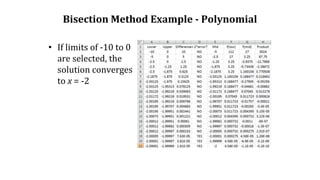
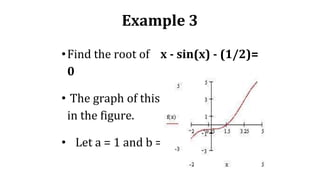
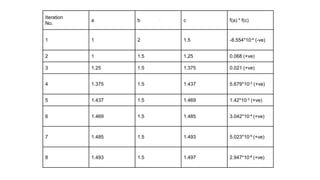
48. Example
Lets look for a solution to the equation x3-2x-3=0.
We consider the function f(x)=x3-2x-3
On the interval [0,2] the function is negative at 0 and positive at 2. This means that a=0 and b=2
(i.e. f(0)f(2)=(-3)(1)=-3<0, this means we can apply the algorithm).
This is negative and we will make the a =3/2 and b is
the same and apply the same thing to the interval
[3/2,2].
This is negative and we will make the a =54/29 and b is
the same and apply the same thing to the interval
[54/29,2].

49. Merits & Demerits
● Merits
As the interval becomes small, the
interior point generally becomes much closer
to root.
Faster convergence than bisection.
Often superior to bisection.

50. Demerits
● Demerits
It can’t predict number of iterations to
reach a give precision.
It can be less precise than bisection – no
strict precision guarantee.

51. ● Though the difference between Bisection and
False Position Method is little but for some
cases False Position Method is useful and for
some problems Bisection method is
effective….
● In fact they both are necessary to solve any
equation by ‘Bracketing method’.