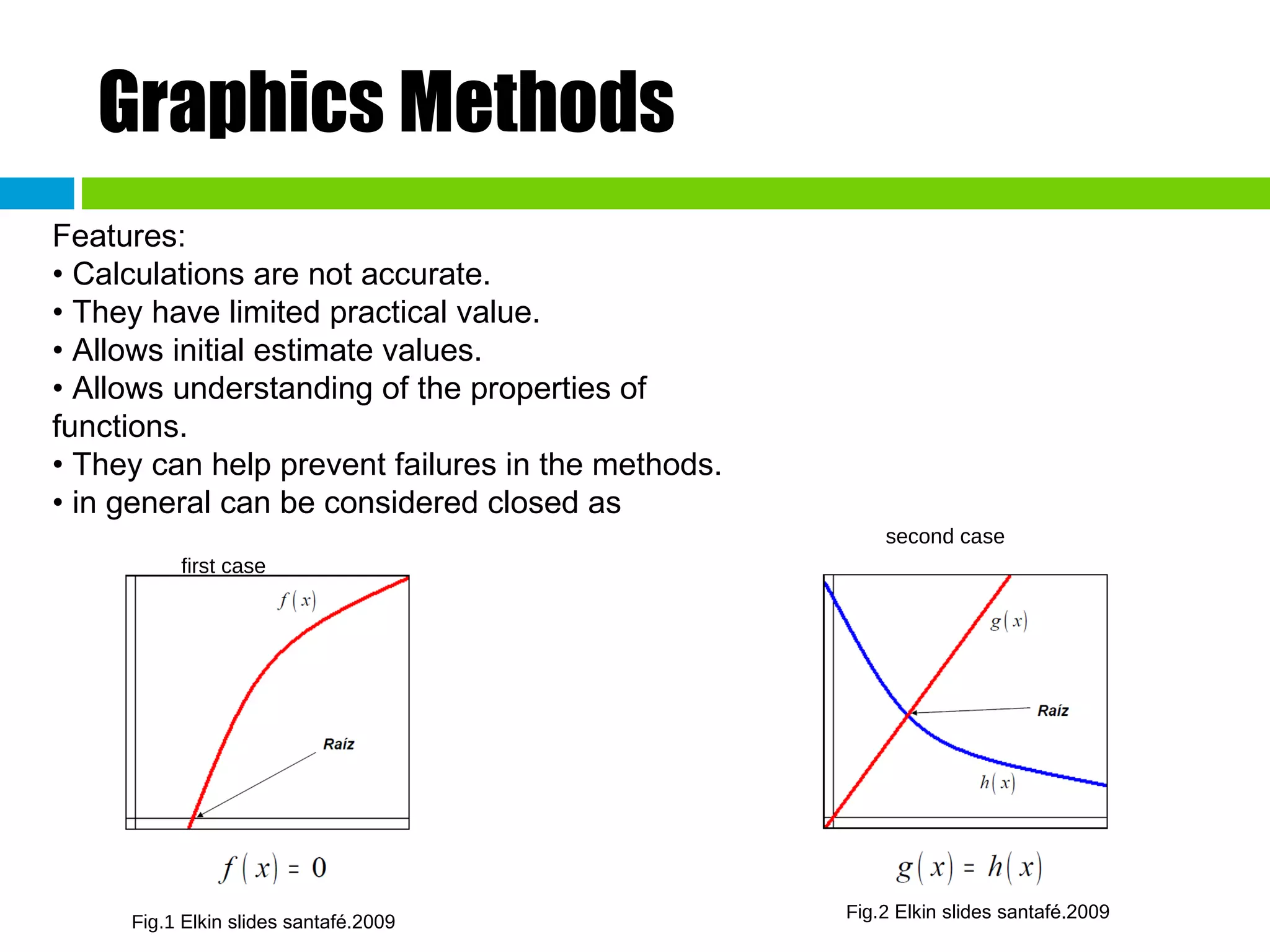
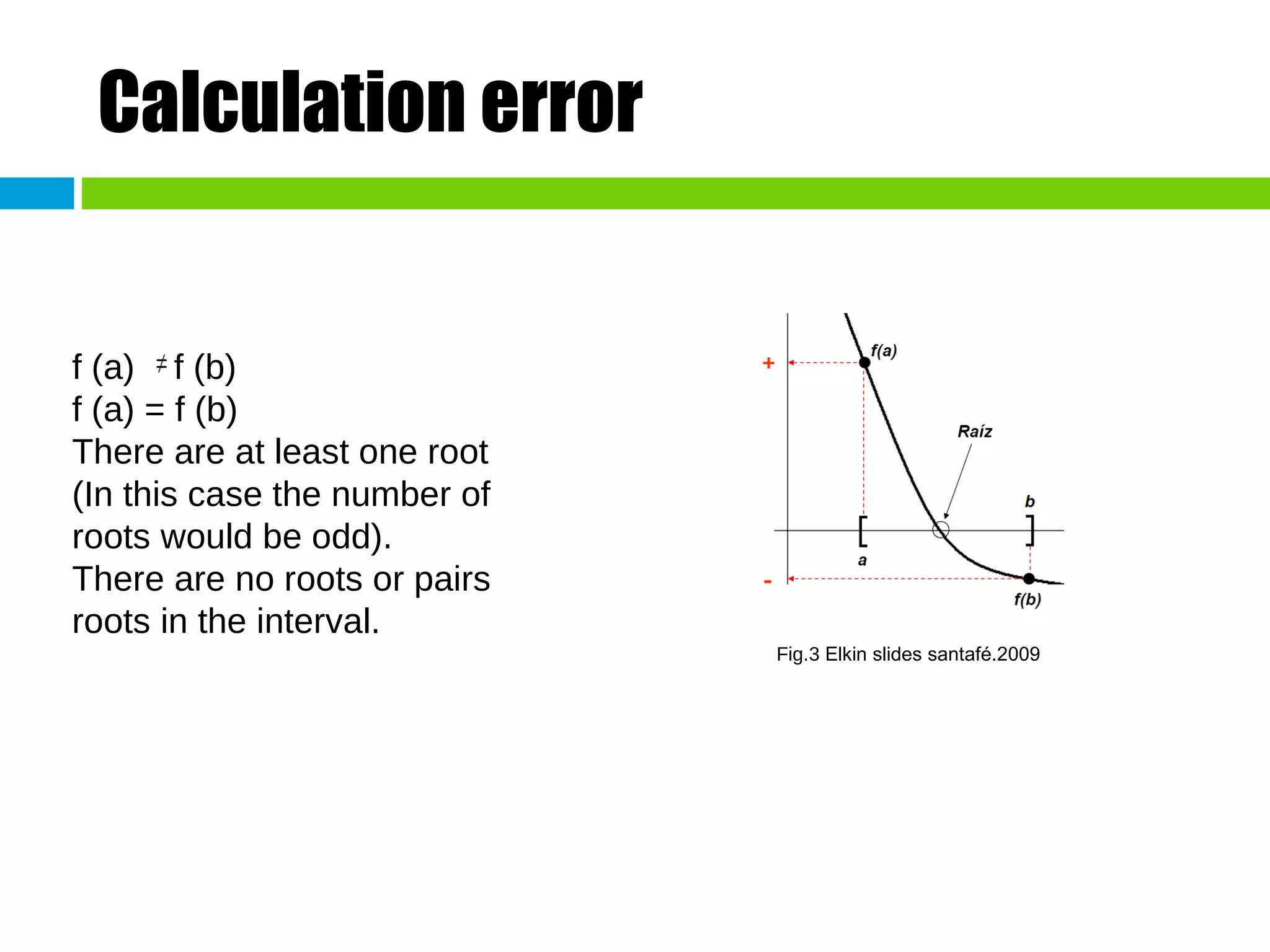
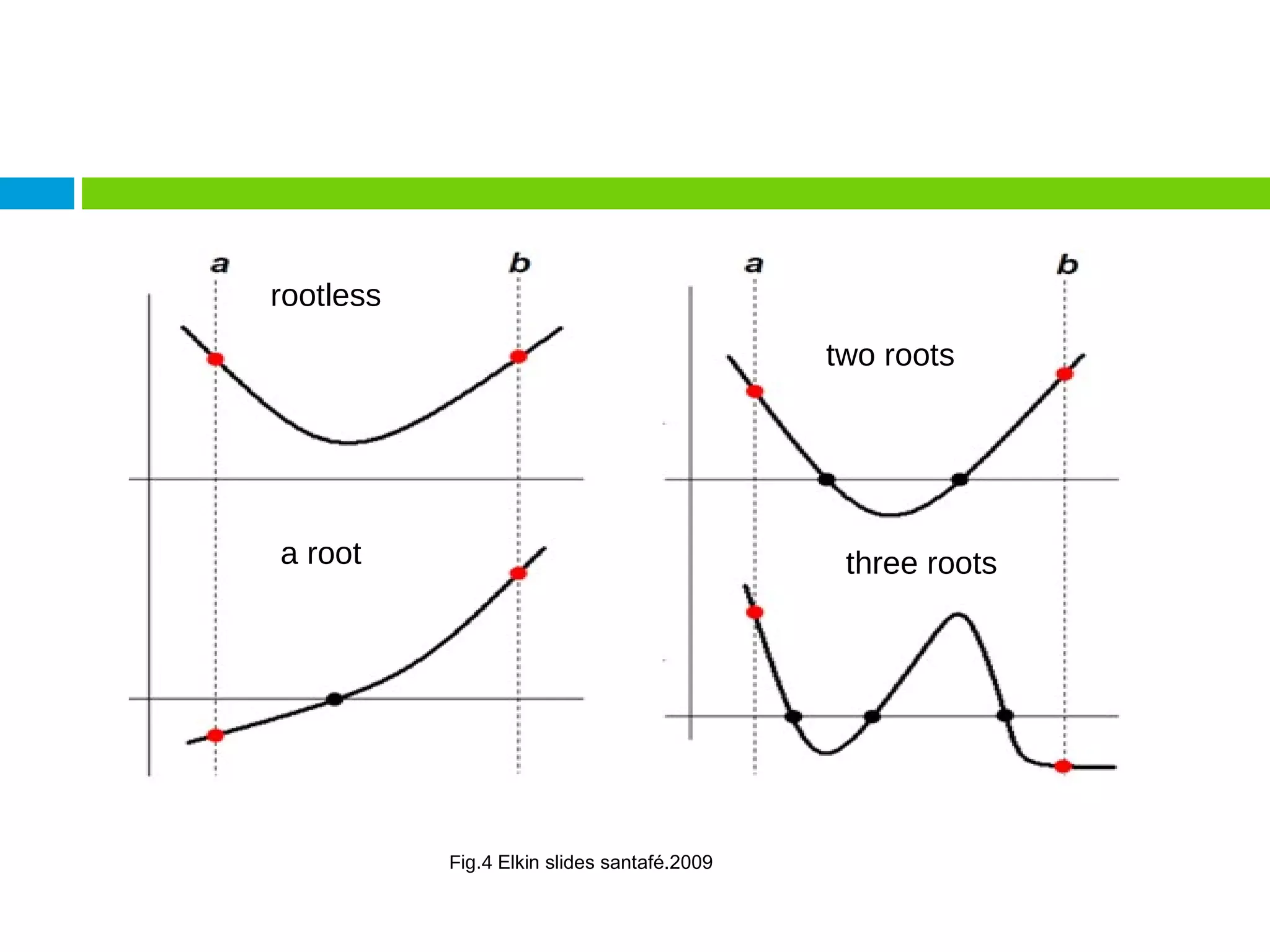
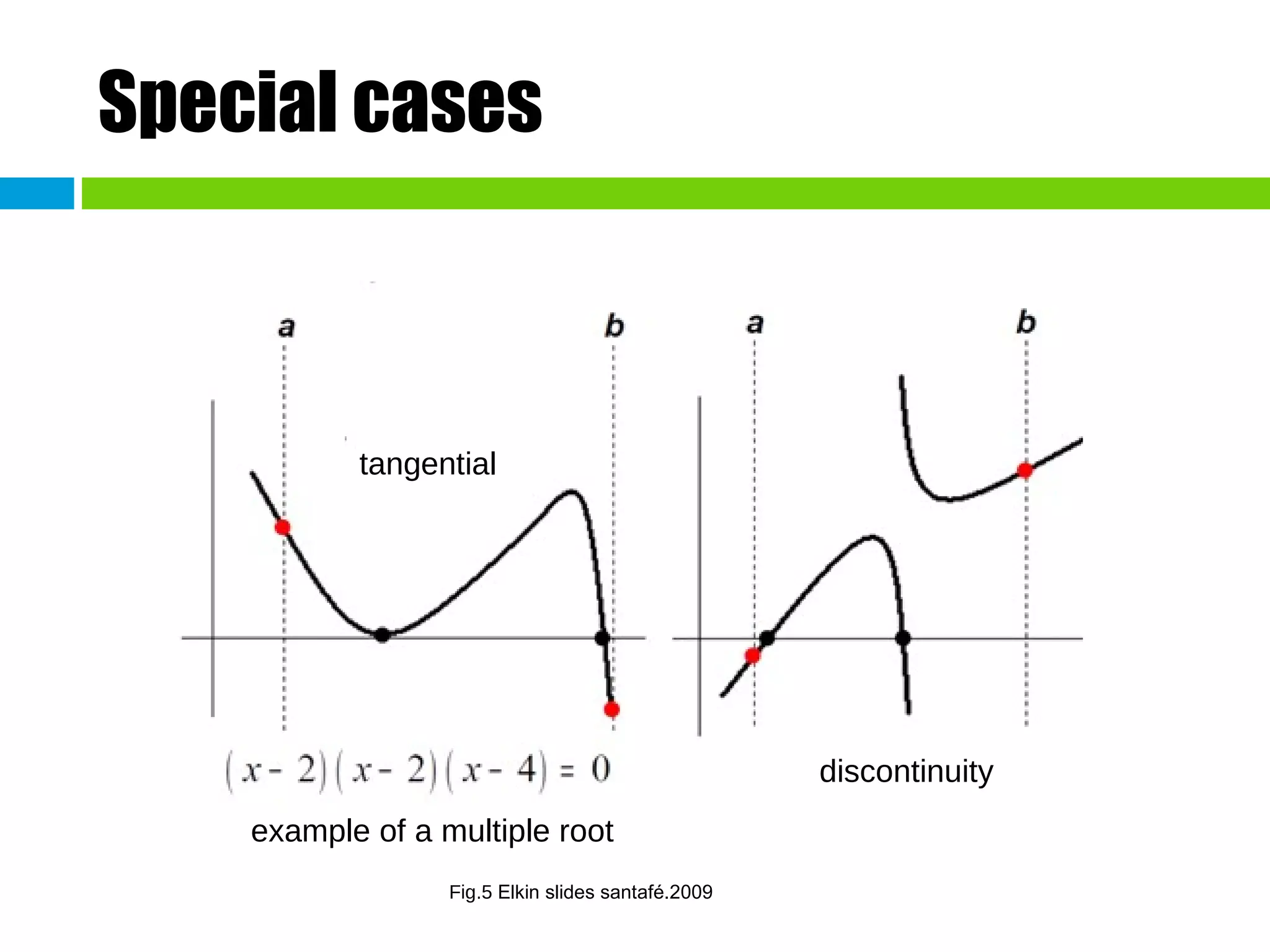
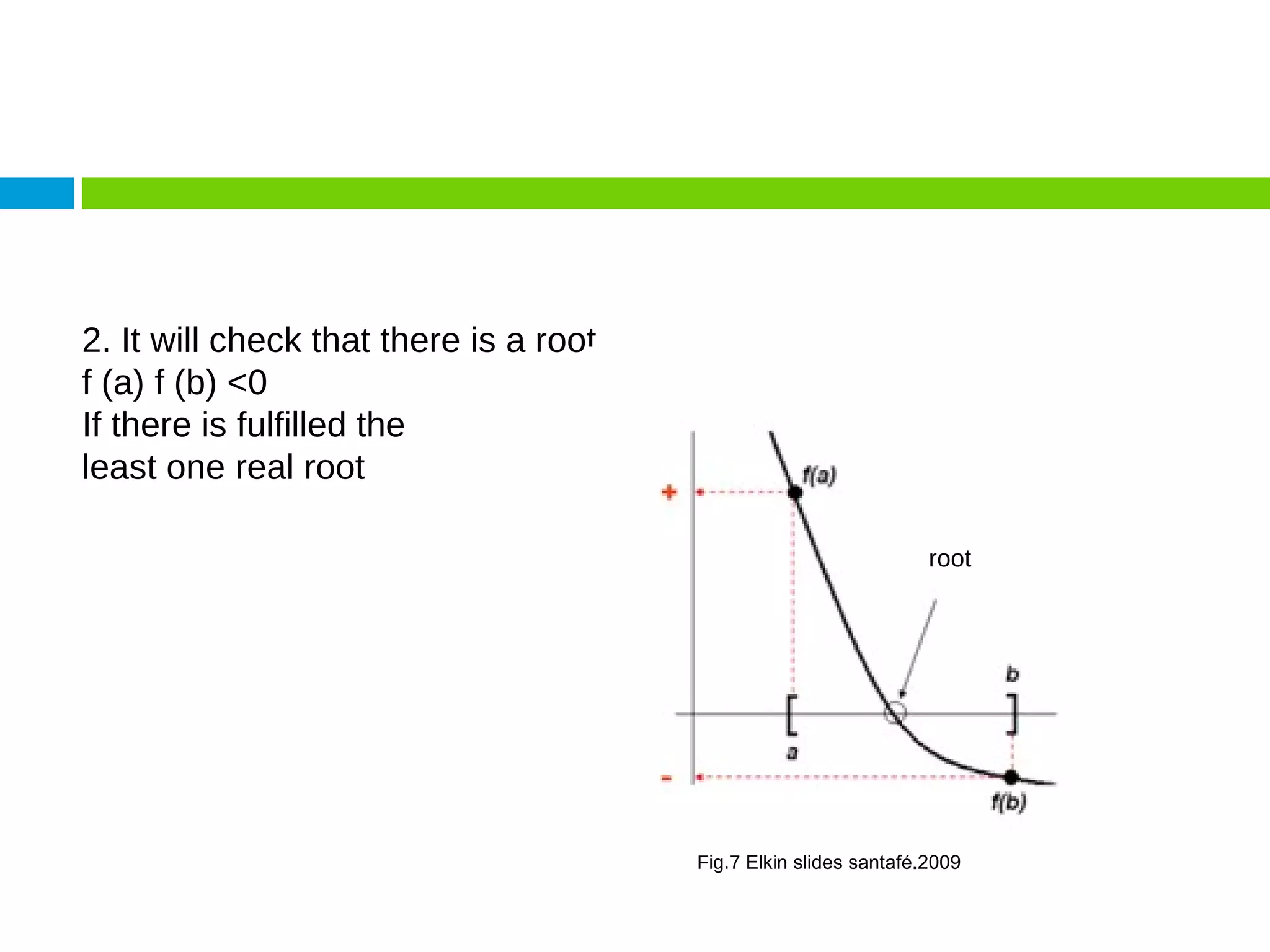
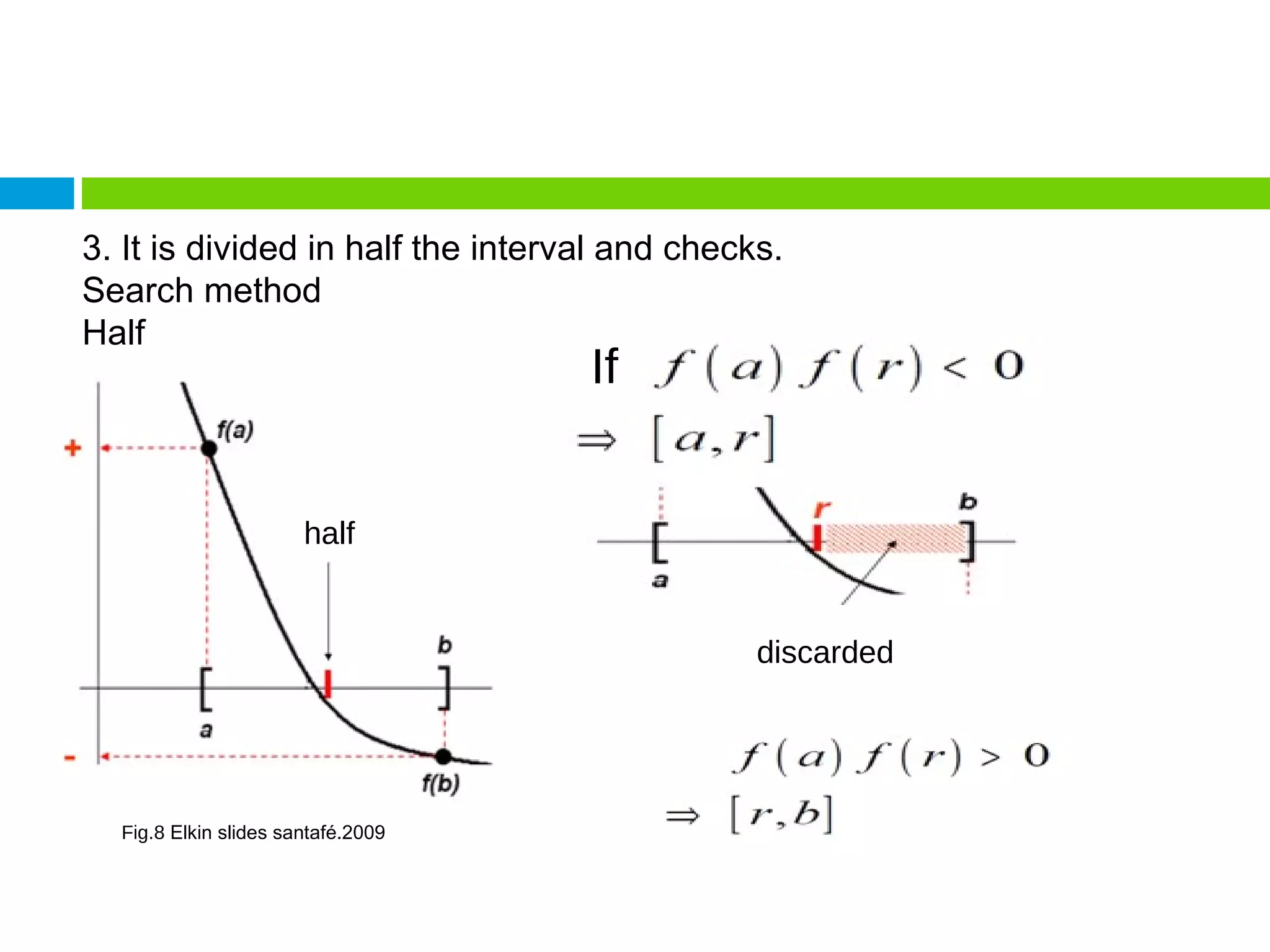
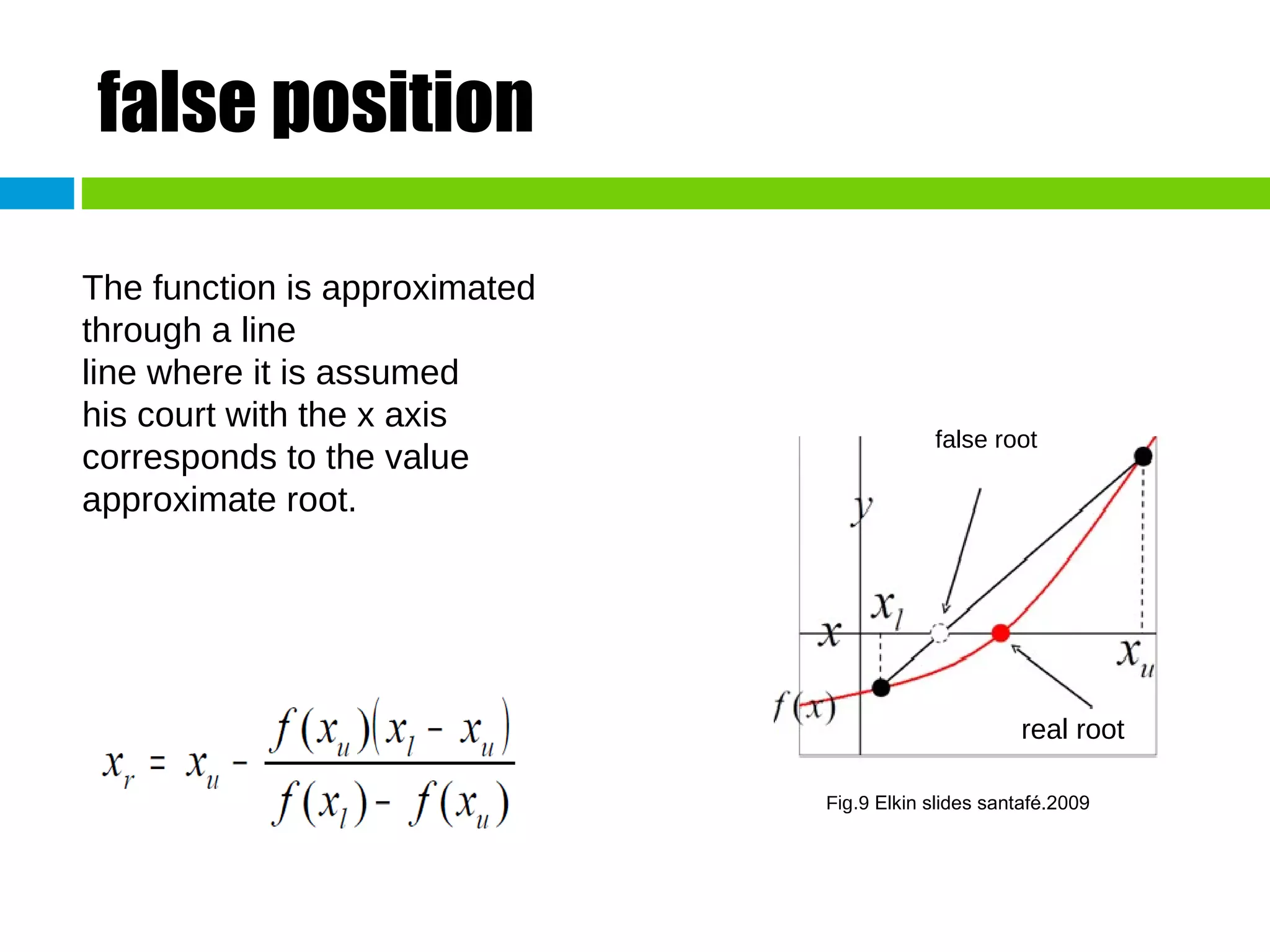
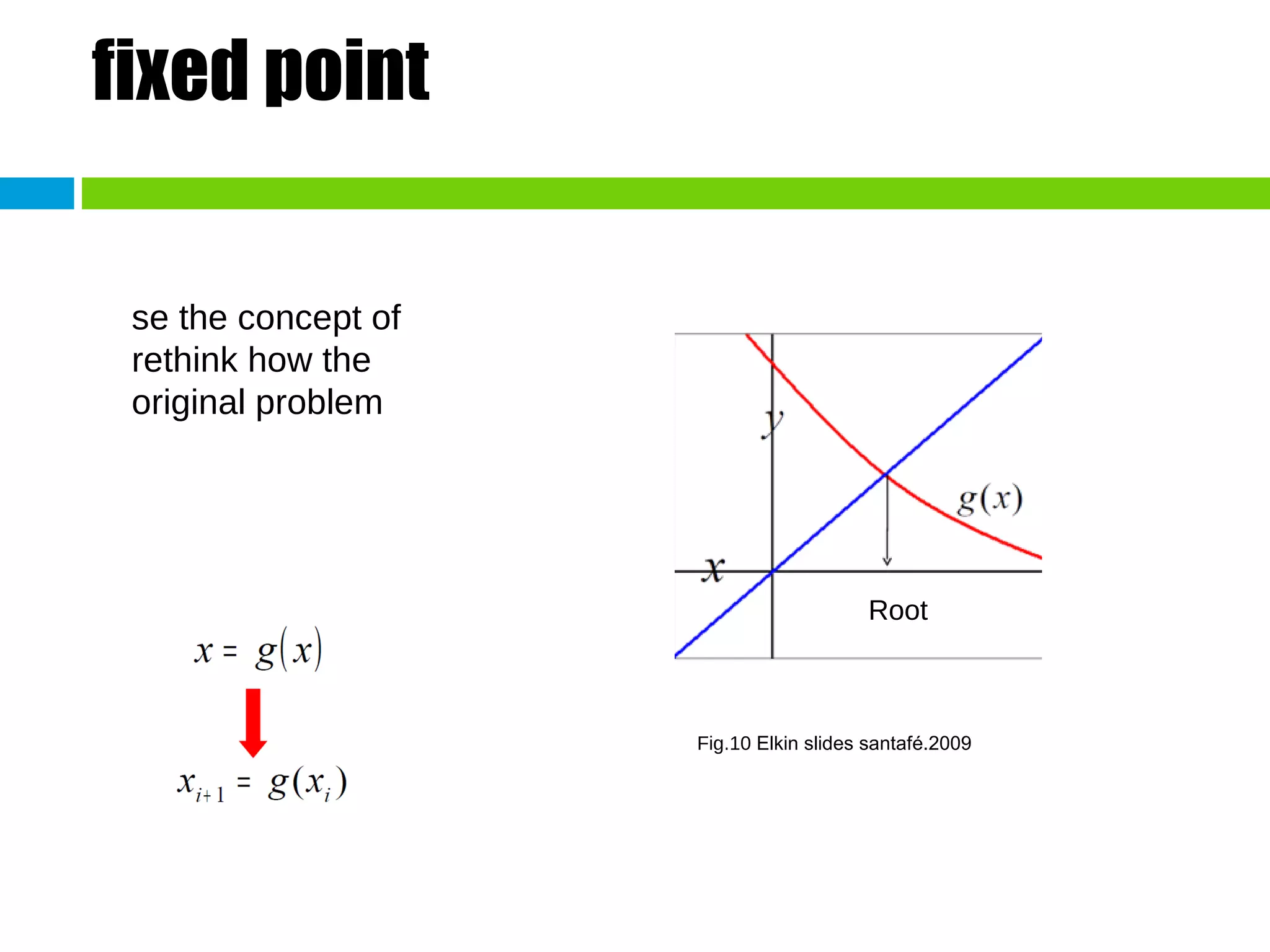
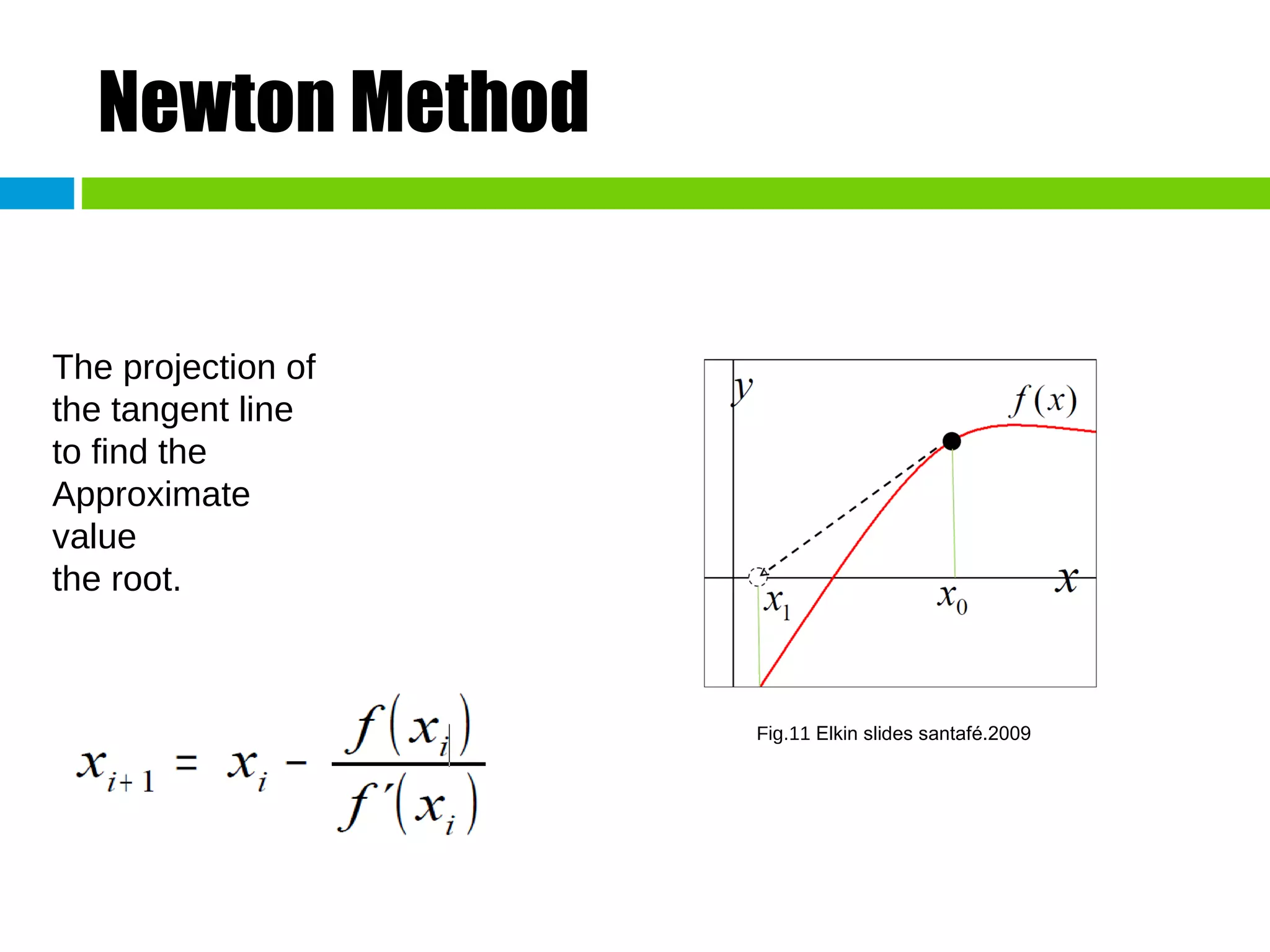
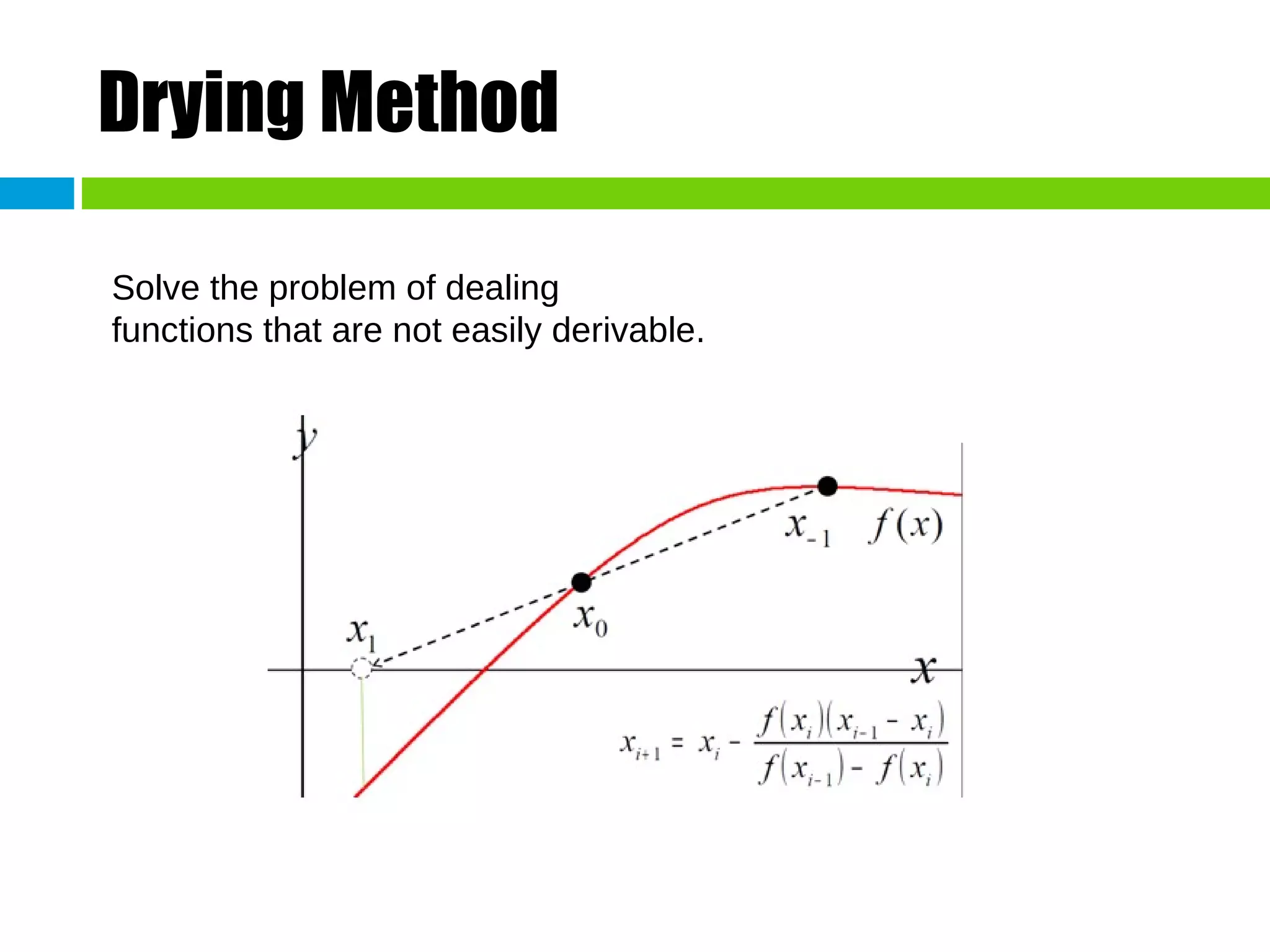
This document discusses methods for finding the roots of equations. It begins by explaining the importance of determining roots and how it relates to other mathematical problems. It then outlines different types of methods including graphical methods, which provide initial estimates but lack precision, and closed methods, which limit the search domain. Specific closed methods discussed include bisection, false position, fixed point, Newton-Raphson, and secant methods. Graphics are provided to illustrate each method.

1. ROOTS OF EQUATIONS

2. General Purpose

3. Introduction The determination of the roots of an equation is one of the oldest problems in mathematics and there have been many efforts in this regard. Its importance is that if we can determine the roots of an equation we can also determine the maximum and minimum eigenvalues of matrices, solving systems of linear differential equations, etc ... The determination of the solutions of the equation can be a very difficult problem. If f (x) is a polynomial function of grade 1 or 2, know simple expressions that allow us to determine its roots. For polynomials of degree 3 or 4 is necessary to use complex and laborious methods. However, if f (x) is of degree greater than four is either not polynomial, there is no formula known to help identify the zeros of the equation (except in very special cases).

4. Types of Methods Graphics Methods • Open methods • Methods Closed

5. Graphics Methods Features: • Calculations are not accurate. • They have limited practical value. • Allows initial estimate values. • Allows understanding of the properties of functions. • They can help prevent failures in the methods. • in general can be considered closed as first case second case Fig.1 Elkin slides santafé.2009 Fig.2 Elkin slides santafé.2009

6. Calculation error f (a) f (b) f (a) = f (b) There are at least one root (In this case the number of roots would be odd). There are no roots or pairs roots in the interval. Fig.3 Elkin slides santafé.2009

7. rootless a root two roots three roots Fig.4 Elkin slides santafé.2009

8. Special cases tangential discontinuity example of a multiple root Fig.5 Elkin slides santafé.2009

9. Closed Methods They are limiting the search domain. Most known are: • Bisection Method • Method of False Position

10. Bisection Method Also known as method: • Binary Court. • Partition. • Bolzano. It is a type of incremental search is based on dividing the always in the middle interval and the change of sign on interval. Search method 1. You must define an initial interval bounded. Fig.6 Elkin slides santafé.2009

11. 2. It will check that there is a root. f (a) f (b) <0 If there is fulfilled the least one real root root Fig.7 Elkin slides santafé.2009

12. 3. It is divided in half the interval and checks. Search method Half If discarded half Fig.8 Elkin slides santafé.2009

13. 4. We review the stopping criterion. Failure to comply is the search continues. The method can be slow in 2 ways: • With the maximum number of iterations. • When you reach the% E. present present previous

14. Advantages and Disadvantages ADVANTAGES • You are guaranteed the convergence of the root lock. • Easy implementation. • management has a very clear error. DISADVANTAGES • The convergence can be long. • No account of the extreme values (dimensions) as possible roots.

15. false position The function is approximated through a line line where it is assumed his court with the x axis corresponds to the value approximate root. false root real root Fig.9 Elkin slides santafé.2009

16. Open Methods They are limiting the search domain. Most known are: • Fixed Point Method • Newton Raphson Method • Drying Method

17. fixed point se the concept of rethink how the original problem Root Fig.10 Elkin slides santafé.2009

18. Newton Method c c The projection of the tangent line to find the Approximate value the root. Fig.11 Elkin slides santafé.2009

19. Drying Method Solve the problem of dealing functions that are not easily derivable.

20. Bibliography http://www.uv.es/diaz/mn /node17. ht ml Elkin slides santafé.2009 http://sites.google.com/site/metnumeric/Home/2-aproximacion-numerica-errores-y-metodos-numericos-iniciales