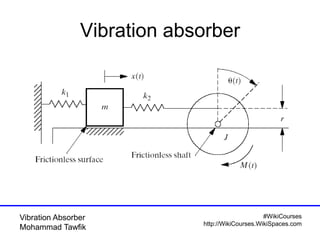
This document discusses vibration absorbers for damping vibrations in structures. It presents the equations of motion for a 2-degree of freedom system with an absorber and goes through the process of obtaining the solution. It is shown that for the primary system to be stationary, the excitation frequency must match the natural frequency of the absorber mass-spring system. Homework problems are assigned to further analyze systems with different excitation frequencies using the presented approach and modal decomposition.

1. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
Vibration Absorber
The first passive damping
technique we will learn!

2. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
For a 2-DOF System
• For the shown 2-DOF
system, the equations
of motion may be
written as:
• Where:
fxx  KM 







2
1
f
f
f

3. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
For Harmonic Excitation
• We may write the
equation for each of
the excitation
frequency in the form
of:
• Then we may add
both solutions!
 







0
11 tCosf
KM

xx
 






tCosf
KM
22
0

xx

4. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
Consider the first force
• We may write the
equation in the form:
• And the solution in
the form:
• Which will give:
 tCosfKM 1
0
1






 xx
 tCos
x
x








2
1
x
  xx 2
2
12
 






 tCos
x
x


5. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
The equation of motion becomes
• Get x1() and find out when does it equal
to zero!





































00
0 1
2
1
22
221
2
2
1
2
f
x
x
kk
kkk
m
m



6. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
Using the Dynamic Stiffness
Matrix
• Writing down the dynamic stiffness matrix:
Getting the inverse:




















0
1
2
1
22
2
2
2211
2
f
x
x
KmK
KKKm


   




















0
1
2
222
2
211
2
211
2
2
222
2
2
1 f
KKmKKm
KKmK
KKm
x
x




7. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
Obtaining the Solution
• Multiply the inverse by the right-hand-side
• For the first degree of freedom:
  
 





 







12
122
2
21
2
21212
4
212
1 1
fK
fKm
KKKmKKmmmx
x 

 
  
0
21
2
21212
4
21
122
2
1 



KKKmKKmmm
fKm
x



8. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
Vibration Absorber
• For the first degree of freedom to be
stationary, i.e. x1=0
• The excitation frequency have to satisfy:
• Note that this frequency is equal to the
natural frequency of the auxiliary spring-
mass system alone
2
2
m
K


9. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
Vibration absorber

10. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
Vibration absorber

11. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
Homework #2
• Repeat the example of this lecture using
f2=f3=0 and f1=1 AND f1=f2=0 and f3=1
• Plot the response of each mass for each
of the excitation functions
• Comment on the results in the lights of
your understanding of the concept of
vibration absorber

12. #WikiCourses
http://WikiCourses.WikiSpaces.com
Vibration Absorber
Mohammad Tawfik
Homework #2 (cont’d)
• Use modal decomposition
(diagonalization) to obtain the same
results.