This document discusses several numerical methods for finding the roots or zeros of nonlinear equations, including bracketing methods like bisection that repeatedly decrease an interval containing the solution, open methods like Newton-Raphson that require a good initial guess, and fixed-point iteration that rewrites the equation as x=g(x) and iteratively applies the function. Examples are provided to illustrate applying bisection, false position, Newton's method, secant method, and fixed-point iteration to solve specific equations numerically.

1. Chapter 2 Solving Nonlinear Equations
Consider a scalar-valued function f (x) and the corresponding equation
f (x)= 0.
- A solution (or a root) to this equation is the value of x that satisfies this
equation.
- This solution is the point on the x-axis where f (x) crosses or touches the
x-axis.
- Then only one of the following can occur.
f(x) has a unique solution
f(x) has no solution
f(x) has many (can be infinitely many) solutions

2. Approaches for finding roots of equations numerically
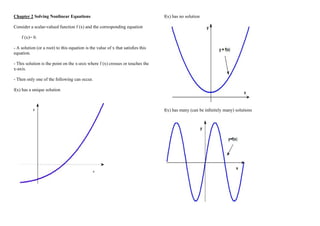
Consider again the equation f (x)= 0.
Bracketing methods
- Use an initial interval that contains the solution
- Repeatedly decrease the size of this interval to get as close to the exact
solution as possible
- Always converge to a solution
- Examples: Bisection method, Falsi method
Open methods
- Require a “good” initial guess (close enough to the true solution)
- May not converge to a solution (depending on the initial guess).
- If the open methods converges to a solution, it is usually more efficient than
the bracketing methods (i.e. converge faster)
- Example: Newton-Raphson method, secant method, fixed-point iteration
Bisection Method:
Step 1: Find an interval [a, b] such that, for the root 0,
=
)
(x
f 
f (a)f (b) < 0
Step 2: Given [a, b], compute approximate solution by using the midpoint:
2
~ b
a
x


Step 3: Decrease the interval:
If 0
)
~
(
)
( 
x
f
a
f , set x
b ~

If 0
)
~
(
)
( 
x
f
a
f , set x
a ~

Update new interval [a, b] and go back to Step 2.
Given [a, b] and TOL, if n is the number of iterations in Bisection method
TOL
a
b
n

 2
log
Example Let a = 0.1 and b = 1.0. Suppose the equation f (x)= 0 has a root
in the interval [a, b]. How many steps of the bisection method are needed to
determine the root with an error of at most 0.5 x 10-8
if [a, b] is used as an
initial interval?

3. Example Compute the approximate root of x4
- 2x3
- 10 = 0 by using three
iterations of the bisection method with the initial interval [1, 3]. Calculate the
residual, absolute error and relative error in each iteration

4. Example Suppose we want to determine where the graphs of y = 3x and y =
ex
intersect on the interval [0, 1].Compute the approximate root from the first
three iterations with the initial interval [0, 1] by using the bisection method.
Calculate the residual, absolute error and relative error in the last iteration.

5. False Position Method
Step 1: Find an interval [a, b] such that, for the root 0,
=
)
(x
f 
f (a)f (b) < 0
Step 2: Given [a, b], compute approximate solution by using:
)
(
)
(
)
(
)
(
~
a
f
b
f
a
bf
b
af
x



Step 3: Decrease the interval:
If 0
)
~
(
)
( 
x
f
a
f , set x
b ~

If 0
)
~
(
)
( 
x
f
a
f , set x
a ~

Update new interval [a, b] and go back to Step 2.
Example Compute the approximate root of x4
- 2x3
- 10 = 0 by using three
iterations of the false position method with the initial interval [1, 3].
Calculate the absolute error and relative error in each iteration

6. Newton’s Method
)
(
)
(
1
1
1






j
j
j
j
x
f
x
f
x
x
Example Suppose we want to determine where the graphs of y = 3x and y =
ex
intersect on the interval [0, 1].Compute the approximate root by using
Newton’s Method with the initial value x0 = 1 repeated until the residual error
is less than 10-4
. How many iterations are required to perform?

7. Secant Method
)
(
)
(
)
(
1
1
1







j
j
j
j
j
j
j
x
f
x
f
x
x
x
f
x
x
Example Compute the approximate root of x4
- 2x3
- 10 = 0 by using three
iterations of the secant method with the initial values x0 = 1, x1 = 2. Calculate
the absolute error in the last iteration.

8. Example: The following table shows the approximated root of
[0,1]
x
0
3 

 x
e x
by using Secant method with the initial points x0 = 0, x1 = 1.
- Determine the values of a1, b2, c3 in the table.
- Suppose we want to have the approximation with absolute error less than
5 x10-2
. How many iterations has to be used?

9. Fixed-Point Iteration Method
Re-write the equation as x = g(x)
• Choose a starting value x0
• While(stopping condition not met)
xi+1 = g(xi)
Example: Apply the fixed-point procedure to approximate a root of f (x)= 0
where f (x)= cos(x) - xex
with
x
xe
x
x
g
e
x
x
g
x
x




)
cos(
)
(
)
cos(
)
(
2
1
and starting with x0 = 1 for both g1 and g2.