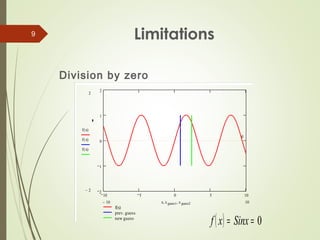
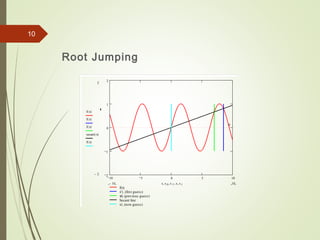
The document discusses the secant method for finding the roots of non-linear equations. It introduces the secant method which uses successive secant lines through points on the graph of a function to better approximate roots. The methodology section explains that a secant line is defined by two initial points and the next point is where the secant line crosses the x-axis. The algorithm involves calculating the next estimate from the two initial guesses and checking if the error is below a tolerance level. Applications include using the secant method for earthquake engineering analysis and limitations include potential division by zero errors or root jumping.

1. University of Engineering and Technology, Lhr
Dept. of Computer Science and Engg.
Numerical Analysis
(Presentation)
Instructed by: SIR Ahmad Awais
Members: Hafiz Hassaan Tariq (2015-CS-67)
Muhammad Umair (2015-CS-5)
Ahmad Afraz Khan(2015-CS-27)
1

2. Secant Method
Problem Statement:
“To find the roots of a non-linear equation with the help of secant
lines”.
Introduction:
In this method roots are found using an algorithm, that uses
succession of roots of secant lines to better approximate a root of
a function. This method can be thought of as a finite difference of
Newton’s Method.
2

3. 3
Methodology
A secant line is defined by using two points on graph of
a function f(x). It is necessary to choose these two initial
points as xi and xi-1. Then next point xi+1 is obtained by
computing x-value at which the secant line passing through
the points (xi, f(xi)) and (xi-1, f(xi-1)) has a y-coordinate of
zero.
f(x)
f(xi)
f(xi-1)
xi+1 xi-1 xi
X
B
C
E D A

4. Secant Method – Derivation4
)()(
))((
1
1
1
−
−
+
−
−
−=
ii
iii
ii
xfxf
xxxf
xx
The Geometric Similar Triangles
f(x)
f(xi)
f(xi-1)
xi+1 xi-1 xi
X
B
C
E D A
11
1
1
)()(
+−
−
+ −
=
− ii
i
ii
i
xx
xf
xx
xf
DE
DC
AE
AB
=
The secant method can also be derived from geometry:
can be written as
On rearranging, the secant
method is given as

5. Algorithm
Step 1
5
Calculate the next estimate of the root from two initial
guesses
)()(
))((
1
1
1
−
−
+
−
−
−=
ii
iii
ii
xfxf
xxxf
xx
Find the absolute relative approximate error
010
1
1
x
- xx
=
i
ii
a ×∈
+
+

6. Step 2
Find if the absolute relative approximate error is
greater than the prespecified relative error
tolerance.
If so, go back to step 1, else stop the algorithm.
Also check if the number of iterations has exceeded
the maximum number of iterations.
6

7. 7 Applications
• Secant method is one of the analytical procedure
available to earthquake engineers for predicting
earthquake performance and structures.
• Secant method is used to develop linear dynamic
analysis model to have the potential to influence the
behavior of the structure in non-linear range.
• It is used for non-linear push over analysis, which
defines the force-displacement relationship of the walls in
the building under lateral load.

8. Advantages
• It converges faster than a linear rate so it is more rapidly
convergent.
• Requires two guesses that do not need to bracket the root.
• It doesn’t require use of derivative of a given function
because in some practical cases, derivatives become very
hard to find.
• It requires only one function evaluation per iteration as
compared to Newton’s method which requires two.
8

9. Limitations9
10 5 0 5 10
2
1
0
1
2
f(x)
prev. guess
new guess
2
2−
0
f x( )
f x( )
f x( )
1010− x x guess1, x guess2,
Division by zero
( ) 0== Sinxxf

10. Root Jumping
10
10 5 0 5 10
2
1
0
1
2
f(x)
x'1, (first guess)
x0, (previous guess)
Secant line
x1, (new guess)
2
2−
0
f x( )
f x( )
f x( )
secant x( )
f x( )
1010− x x 0, x 1', x, x 1,