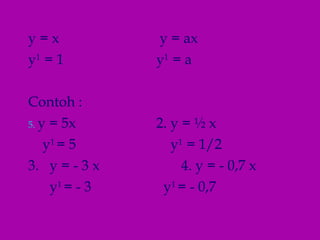
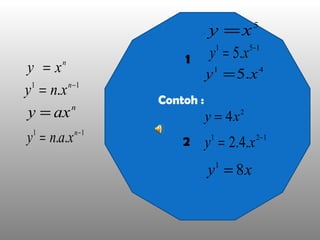
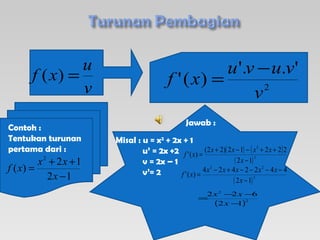
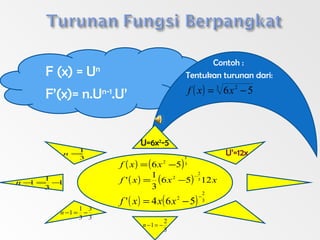
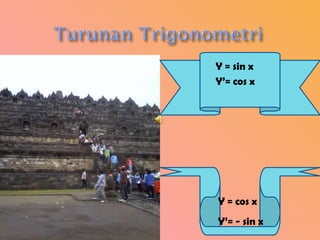
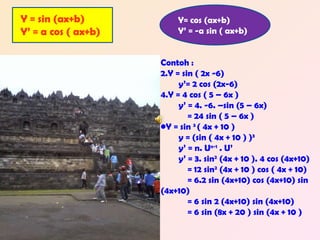
Dokumen ini menjelaskan konsep turunan dan memberikan contoh perhitungan turunan fungsi matematis seperti polinomial dan trigonometri. Juga disertakan metode untuk menentukan persamaan garis singgung pada kurva menggunakan turunan. Contoh-contoh yang disediakan meliputi fungsi sederhana serta penerapan aturan rantai.

1. Oleh : Fatimah S.Pd SMA Muhammadiyah 5 Jakarta

2. y = k ; k = konstanta y 1 = 0 Contoh : y = 3 y 1 = 0 y = - 3 y 1 = 0

3. y = x y = ax y 1 = 1 y 1 = a Contoh : y = 5x 2. y = ½ x y 1 = 5 y 1 = 1/2 3. y = - 3 x 4. y = - 0,7 x y 1 = - 3 y 1 = - 0,7

4. Contoh : 1 2

5. u.v = u’.v + u.v’ Contoh : Tentukan turunan pertama dari : (x+1)(x-2) Jawab : Misal : u = x+1 u’=1 v = x-2 v’=1 Maka, Turunannya = 1.(x-2) + (x+1).1 = x – 2 + x +1 = 2x - 1

6. Contoh : Tentukan turunan pertama dari : Jawab : Misal : u = x 2 + 2x + 1 u’ = 2x +2 v = 2x – 1 v’= 2

7. F (x) = U n F’(x)= n.U n-1 .U’ Contoh : Tentukan turunan dari: U=6x 2 -5 U’=12x

8. Y = sin x Y’= cos x Y = cos x Y’= - sin x

9. Y = sin (ax+b) Y’ = a cos ( ax+b) Y= cos (ax+b) Y’ = -a sin ( ax+b) Contoh : Y = sin ( 2x -6) y’= 2 cos (2x-6) Y = 4 cos ( 5 – 6x ) y’ = 4. -6. –sin (5 – 6x) = 24 sin ( 5 – 6x ) Y = sin 3 ( 4x + 10 ) y = (sin ( 4x + 10 ) ) 3 y’ = n. U n-1 . U’ y’ = 3. sin 2 (4x + 10 ). 4 cos (4x+10) = 12 sin 2 (4x + 10 ) cos ( 4x + 10) = 6.2 sin (4x+10) cos (4x+10) sin (4x+10) = 6 sin 2 (4x+10) sin (4x+10) = 6 sin (8x + 20 ) sin (4x + 10 )

10. Jika diketahui suatu kurva y = f (x) Maka f’(x) = dy/dx = gradien garis singgung pada titik P (x,y) pada kurva. Persamaan garis singgung dirumuskan dengan : y-y 1 = y’(x – x 1 ) , atau : y-y 1 = m(x – x 1 )

11. Tentukan persamaan garis singgung pada kurva y = 3x 2 + 4x – 5 di titik yang berabsis 1 ! Jawab : x = 1 -> y = 3.1 2 + 4.1 – 5 = 3 + 4 – 5 = 2, didapat titik ( 1,2 ) y = 3x 2 + 4x – 5 dy/dx = y’ = 6x + 4 m = 6.1 +4 = 10 Jadi, persamaan garis singgung di titik ( 1,2 ) : y-y 1 = m(x – x 1 ) y – 2 = 10 (x – 1 ) y-2 = 10x – 10 y = 10x – 10 + 2 = 10 x - 8