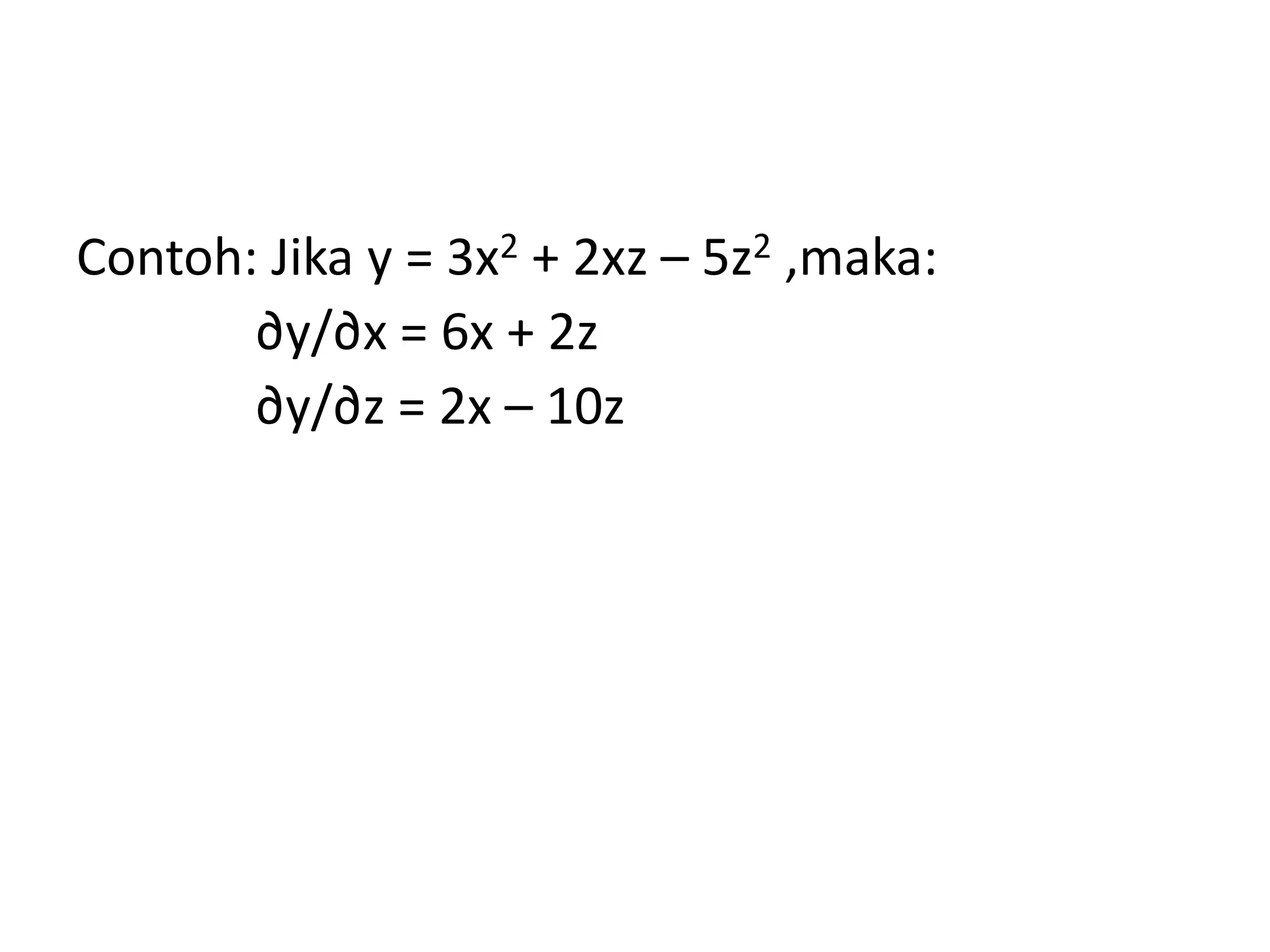Dokumen ini membahas tentang diferensial dan optimalisasi fungsi majemuk, termasuk definisi diferensial parsial dan contoh penerapannya dalam menentukan titik maksimum dan minimum suatu fungsi. Juga dijelaskan cara menentukan titik ekstrim dan nilai fungsi pada titik ekstrim untuk fungsi satu atau lebih variabel.

2. Diferensial & Optimalisasi
Diferensial Fungsi Majemuk
Optimalisasi
Penerapan dalam ekonomi

3. Parsial Diferensial
• Sebuah fungsi yg hanya mengandung satu variabel
bebas hanya akan memiliki satu macam turunan
Jika y = f(x) maka turunan y terhadap x: y’ = dy/dx
• Sedangkan jika fungsi yg bersangkutan memiliki
lebih dari satu variabel bebas, maka turunannya
akan lebih dari satu macam, tergantung jumlah
variabel bebasnya.
• Diferensial Parsial merTeknik ini digunakan untuk
suatu fungsi lebih dari satu variabel. z = f(x, y)
atau z = f( u, v, x) dst

4. Banyak kejadian terdiri dari beberapa variabel.
Contoh: Qd = f(h, hkl, sK, i,)
dimana h = harga komoditi itu sendiri
hkl = harga komoditi lain
sK = selera konsumen
i = income
Misal : y = f(x , z), bila “z” dianggap tetap, maka “y” hanya
merupakan fungsi “x”, sehingga derivatif “y” ke “x” dapat
dihitung.
Sedangkan derivatifnya disebut derivatif parsial dari “y”
ke “x” dan dilambangkan dengan:
∂z/∂x atau ∂f/∂x atau fx

5. Demikian juga jika “x” dianggap tetap, maka
derivatif parsial ke “y” dapat dihitung, dan
dilambangkan dgn:
∂z/∂y atau ∂f/∂y atau fy

6. Contoh: Jika y = 3x2 + 2xz – 5z2 ,maka:
∂y/∂x = 6x + 2z
∂y/∂z = 2x – 10z

7. Contoh: y = x3 + 5z2 – 4x 2z – 6x z2 –8 z - 7
(1) ∂y/∂x = fX = 3x2 -8xz -6z2
(2) ∂y/∂z = fz = 10z – 4x2-12xz + 8
∂y/∂x trhdp x  ∂2z/∂x2 = fXX = 6x-8z
∂y/∂x trhdp z ∂2y/∂x∂z = fxz = -8x – 12 z
∂y/∂z trhdp z  ∂2y /∂z2 = fzz = 10-12x
∂y/∂z trhdp x  ∂2z/ ∂z∂x = fzx =-8 x -12 x
∂2y /∂x2 trhdp x  ∂3y /∂x2 = -------?
∂2y /∂x2 trhdp z  ∂3y /∂x2 ∂z = -------?

8. Matematika Ekonomi 8
Maksimum dan minimum
y = f(x)
akan maksimum pada saat:
dy/dx = 0
dan d2y/dx2 < 0
akan minimum pada saat:
dy/dx = 0
dan d2y/dx2 > 0
akan mempunyai titik belok (inflection point) pada:
dy/dx = 0
dan d2y/dx2 = 0

9. Matematika Ekonomi 9
Apabila fungsinya lebih dari dua variabel:
z = f(x, y) atau f(x1, x2),
Maksimum jika
dy/dx = 0, fx = 0
d2y/dx2 < 0, fxx <0
Minimum jika
dy/dx = 0, fx = 0
d2y/dx2 > 0, fxx >0

10. Matematika Ekonomi 10
Apabila fungsinya lebih dari dua variabel:
z = f(x, y) atau f(x1, x2),
Maksimum jika fx
= 0, fy = 0
fxx < 0, fyy < 0
fxxfyy – (fxy)2 > 0
Minimum jika fx
= 0, fy = 0
fxx > 0, fyy > 0
fxxfyy – (fxy)2 > 0

12. Matematika Ekonomi 12
Contoh: Periksa apakah fungsi berikut ini mempu-nyai
titik maksimum, minimum atau titik belok dan hitung
nilai f(x) pada titik tersebut.
y = f(x) = -x2 + 4x + 7
dy/dx = -2x + 4 = 0; nilai x = 2
d2y/dx2 = -2 < 0; berarti mempunyai titik maks.
pada x = 2.
nilai ymaks atau f(x)maks = -(2)2 + 4(2) + 7 = 11

13. Matematika Ekonomi 13
Contoh: Tentukan nilai ekstrim (maks/min) dari:
z = x2 + xy + y2 – 3x + 2
selidikilah apakah titik ekstrim dari fungsi tersebut
merupakan titik maksimum atau minimum!
Langkah-langkah:
a. Derivatif pertama: fx = 2x + y – 3
fy = x + 2y
b. fx = 0 dan fy = 0
2x + y – 3 = 0
x + 2y = 0
Dari 2x + y – 3, didapat y = 3 – 2x.
Substitusi y = 3 – 2x ke persamaan x + 2y = 0
didapat x + 2(3 – 2x) = 0; x + 6 – 4x = 0
atau 3x = 6  x = 2.

14. Matematika Ekonomi 14
Untuk x = 2, y = 3 – 2(2) = -1.
Artinya titik (2, -1) merupakan titik maks atau min
c. Uji dengan derivatif kedua:
fxx = 2; fyy = 2; fxy = fyx = 1
fxxfyy – (fxy)2 = 2.2 – 12 = 3 > 0
artinya fungsi z mempunyai titik minimum pada titik (2, -
1).
d. Nilai zmin = (2)2 + (2)(-1) + (-1)2 – 3(2) + 2
= 4 – 2 + 1 – 6 + 2 = -1.

15. Latihan
• Carilah titik ekstrim dari fungsi:
p = 3q2 – 18q + r2 – 8r + 50
selidikilah apakah titik ekstrim dari fungsi
tersebut merupakan titik maksimum atau
minimum!